Lecture
When transmitting messages via communication lines, one always has to use one or another code, that is, the presentation of a message as a series of signals. A well-known example of code can be Morse code accepted in telegraphy for transmitting verbal messages. Using this alphabet, any message is represented as a combination of elementary signals: a dot, a dash, a pause (space between letters), a long pause (space between words).
In general, coding is the state map of one physical system using the state of some other. For example, during a telephone conversation, audio signals are encoded as electromagnetic oscillations, and then decoded again, turning into audio signals at the other end of the line. The simplest case of coding is when both systems 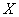 and
and 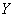 (mapping and imaging) have a finite number of possible states. This is the case when transmitting recorded letters, for example, when wiring. We restrict ourselves to the consideration of this simplest case of coding.
(mapping and imaging) have a finite number of possible states. This is the case when transmitting recorded letters, for example, when wiring. We restrict ourselves to the consideration of this simplest case of coding.
Let there be some system 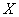 (for example, the letter of the Russian alphabet), which can randomly take one of the states
(for example, the letter of the Russian alphabet), which can randomly take one of the states 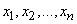 . We want to display it (encode) using another system.
. We want to display it (encode) using another system. 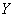 whose possible states
whose possible states 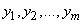 . If a
. If a 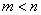 (number of system states
(number of system states 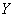 less number of system states
less number of system states 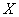 ), then every system state cannot be
), then every system state cannot be 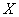 encode using a single system state
encode using a single system state 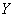 . In such cases, one system state
. In such cases, one system state 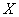 you have to display using a certain combination (sequence) of system states
you have to display using a certain combination (sequence) of system states 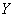 . So, in Morse code letters are displayed with various combinations of elementary characters (dot, dash). The choice of such combinations and the establishment of correspondence between the transmitted message and these combinations is called “coding” in the narrow sense of the word.
. So, in Morse code letters are displayed with various combinations of elementary characters (dot, dash). The choice of such combinations and the establishment of correspondence between the transmitted message and these combinations is called “coding” in the narrow sense of the word.
Codes differ in the number of elementary symbols (signals) from which combinations are formed, in other words, in the number of possible system states. 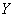 . There are four such elementary characters in Morse code (dot, dash, short pause, long pause). Signals can be transmitted in various forms: light flashes, sending electric current of different duration, sound signals, etc. The code with two elementary symbols (0 and 1) is called binary. Binary codes are widely used in practice, especially when entering information into electronic digital computers operating on a binary number system.
. There are four such elementary characters in Morse code (dot, dash, short pause, long pause). Signals can be transmitted in various forms: light flashes, sending electric current of different duration, sound signals, etc. The code with two elementary symbols (0 and 1) is called binary. Binary codes are widely used in practice, especially when entering information into electronic digital computers operating on a binary number system.
The same message can be encoded in various ways. The question arises about the optimal (most beneficial) encoding methods. It is natural to consider the most advantageous such a code in which the minimum amount of time is spent on sending messages. If the transfer of each elementary character (for example, 0 or 1) spends the same time, then the optimal code will be such that the minimum number of elementary characters will be spent on sending a message of a given length.
Suppose that we have a task: to encode the letters of the Russian alphabet with a binary code so that each letter corresponds to a certain combination of elementary symbols 0 and 1 and that the average number of these symbols per letter of the text is minimal.
Consider the 32 letters of the Russian alphabet: a, b, c, d, d, e, f, z, u, k, l, m, n, o, p, p, c, t, y, f, x, , ш,,, щ, ъ,,, ь,,,,, плюс, плюс, plus a space between words, which we will denote by "-". If, as is customary in telegraphy, one does not distinguish between the letters b and b (this does not lead to different interpretations), then one will get 32 letters: a, b, c, d, e, f, g. h, i, y, k, l, m, n, o, n, p, c, t, y f, x, c, h, w, u, (b, b). s. er, w, i, "-".
The first thing that comes to mind is, without changing the order of the letters, to number them in a row, assigning numbers from 0 to 31 to them, and then transfer the numbering to the binary number system. A binary system is one in which units of different bits represent different degrees of two. For example, the decimal number 12 appears as
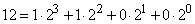
and in the binary system is written as 1100.
Decimal number 25 -
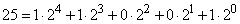
- written in the binary system as 11001.
Each of the numbers 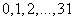 can be represented by a five-digit binary number. Then we get the following code:
can be represented by a five-digit binary number. Then we get the following code:
a - 00000
b - 00001
in - 00010
g - 00011
………
I am 11110
"-" - 11111
In this code exactly 5 elementary symbols are spent on the image of each letter. The question arises whether this simplest code is optimal and is it possible to create another code in which there will be on average less elementary symbols per letter?
Indeed, in our code, the same number of elementary symbols is spent on the image of each letter — the frequently occurring “a”, “e”, “o” or the rarely occurring “u”, “e”, “f”. Obviously, it would be wiser for the frequently occurring letters to be encoded with a smaller number of symbols, and less frequently with more letters.
To compile such a code, obviously, you need to know the frequency of the letters in the Russian text. These frequencies are listed in Table 18.8.1. The letters in the table are arranged in decreasing order of frequencies.
Table 18.8.1.
|
Letter |
Frequency |
Letter |
Frequency |
Letter |
Frequency |
Letter |
Frequency |
|
"-" |
0.145 |
R |
0.041 |
I |
0,019 |
x |
0,009 |
|
about |
0.095 |
at |
0.039 |
s |
0.016 |
well |
0,008 |
|
e |
0.074 |
l |
0.036 |
s |
0.015 |
Yu |
0,007 |
|
but |
0.064 |
to |
0.029 |
b |
0.015 |
sh |
0,006 |
|
and |
0.064 |
m |
0.026 |
b |
0.015 |
c |
0,004 |
|
t |
0.056 |
d |
0.026 |
g |
0.014 |
u |
0,003 |
|
n |
0.056 |
P |
0.024 |
h |
0.013 |
uh |
0,003 |
|
with |
0.047 |
at |
0.021 |
th |
0,010 |
f |
0,002 |
Using this table, you can create the most economical code based on considerations related to the amount of information. Obviously, the code will be the most economical when each elementary symbol will transmit the maximum information. Let us consider an elementary symbol (that is, a signal representing it) as a physical system with two possible states: 0 and 1.
The information that this symbol gives is equal to the entropy of the system and is maximum in the case when both states are equally probable; in this case, the elementary symbol conveys information 1 (two units). Therefore, the basis for optimal coding will be the requirement that the elementary symbols in the encoded text should meet on average equally often.
We present here a method of constructing a code that satisfies the condition; This method is known as the Shannon-Feno code. The idea is that the characters to be coded (letters or combinations of letters) are divided into two approximately equally probable groups: for the first group of characters, the first place of the combination is 0 (the first digit of the binary number representing the character); for the second group - 1. Further, each group is again divided into two approximately equally probable subgroups; for the characters of the first subgroup zero is put in the second place; for the second subgroup - one, etc.
Let us demonstrate the principle of constructing the Shannon-Feno code on the material of the Russian alphabet (Table 18.8.1). Count the first six letters (from "-" to "t"); summing up their probabilities (frequencies), we get 0.498; all other letters (from “n” to “sf”) will have approximately the same probability of 0.502. The first six letters (from “-” to “t”) will have the binary character 0 in the first place. The remaining letters (from “n” to “f”) will have a unit in the first place. Then again we divide the first group into two approximately equally probable subgroups: from “-” to “o” and from “e” to “t”; for all the letters of the first subgroup, put the zero in the second place, and the second subgroup "- one. The process will continue until there is exactly one letter in each division, which will be encoded with a certain binary number. The code building mechanism is shown in Table 18.8 .2, and the code itself is shown in Table 18.8.3.
Table 18.8.2.
|
|
Binary characters |
||||||||
|
Letters |
1st |
2nd |
3rd |
4th |
5th |
6th |
7th |
8th |
9th |
|
- |
0 |
0 |
0 |
|
|
|
|
|
|
|
about |
one |
|
|
|
|
|
|
||
|
e |
one |
0 |
0 |
|
|
|
|
|
|
|
but |
one |
|
|
|
|
|
|||
|
and |
one |
0 |
|
|
|
|
|
||
|
t |
one |
|
|
|
|
|
|||
|
n |
one |
0 |
0 |
0 |
|
|
|
|
|
|
with |
one |
|
|
|
|
|
|||
|
R |
one |
0 |
0 |
|
|
|
|
||
|
at |
one |
|
|
|
|
||||
|
l |
one |
0 |
|
|
|
|
|||
|
to |
one |
|
|
|
|
||||
|
m |
one |
0 |
0 |
0 |
|
|
|
|
|
|
d |
one |
0 |
|
|
|
||||
|
P |
one |
|
|
|
|||||
|
at |
one |
0 |
|
|
|
|
|||
|
I |
one |
0 |
|
|
|
||||
|
s |
one |
|
|
|
|||||
|
s |
one |
0 |
0 |
0 |
|
|
|
||
|
b |
one |
|
|
|
|||||
|
b |
one |
0 |
|
|
|
||||
|
g |
one |
|
|
|
|||||
|
h |
one |
0 |
0 |
|
|
|
|||
|
th |
one |
0 |
|
|
|||||
|
x |
one |
|
|
||||||
|
well |
|
0 |
0 |
|
|
||||
|
Yu |
one |
|
|
||||||
|
sh |
one |
0 |
0 |
|
|||||
|
c |
one |
|
|||||||
|
u |
one |
0 |
|
||||||
|
uh |
one |
0 |
|||||||
|
f |
one |
||||||||
Table 18.8.3
|
Letter |
Binary number |
Letter |
Binary number |
Letter |
Binary number |
Letter |
Binary number |
|
"-" |
000 |
R |
10,100 |
I |
110110 |
x |
1111011 |
|
about |
001 |
at |
10101 |
s |
110111 |
well |
1111100 |
|
e |
0100 |
l |
10110 |
s |
111,000 |
Yu |
1111101 |
|
but |
0101 |
to |
10111 |
b |
111001 |
sh |
11111100 |
|
and |
0110 |
m |
11,000 |
b |
111010 |
c |
11111101 |
|
t |
0111 |
d |
110010 |
g |
111011 |
u |
11111110 |
|
n |
1000 |
P |
110011 |
h |
111100 |
uh |
111111110 |
|
with |
1001 |
at |
110100 |
th |
1111010 |
f |
111111111 |
With the help of table 18.8.3 you can encode and decode any message.
As an example, write the binary code phrase: "information theory"
01110100001101000110110110000
0110100011111111100110100
1100001011111110101100110
Note that there is no need to separate the letters from each other with a special sign, as even without this decoding is performed unambiguously. You can verify this by decoding the following phrase using table 18.8.2:
10011100110011001001111010000
1011100111001001101010000110101
010110000110110110
("Coding method").
However, it should be noted that any error in coding (accidental confusion of the characters 0 and 1) with such a code is destructive, since decoding all the text following the error becomes impossible. Therefore, this encoding principle can be recommended only in the case when errors in encoding and transmission of a message are practically excluded.
A natural question arises: is the code compiled by us in the absence of errors really optimal? In order to answer this question, we will find the average information per one elementary symbol (0 or 1), and compare it with the maximum possible information, which is equal to one binary unit. To do this, we first find the average information contained in one letter of the transmitted text, that is, the entropy per letter:
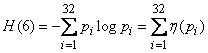 ,
,
Where 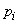 - the probability that the letter will take a certain state ("-", o, e, a, ..., f).
- the probability that the letter will take a certain state ("-", o, e, a, ..., f).
From tab. 18.8.1 we have
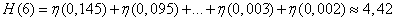
(two units per letter of the text).
Table 18.8.2 determine the average number of elementary characters per letter
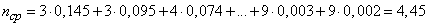 .
.
Dividing entropy  on
on 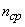 get information on one elementary character
get information on one elementary character
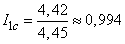 (two units).
(two units).
Thus, the information on one symbol is very close to its upper limit 1, and the code chosen by us is very close to optimal. Staying within the limits of the task of coding by letters, we will not be able to get anything better.
Note that in the case of encoding just binary numbers of letters, we would have an image of each letter with five binary signs and the information for one character would be
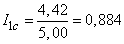 (two units),
(two units),
that is, noticeably less than with optimal letter coding.
However, it should be noted that the coding "spell" is generally not economical. The fact is that there is always a dependency between adjacent letters of any meaningful text. For example, after a vowel in the Russian language can not stand "ъ" or "Ь"; after the sizzling can not stand "I" or "u"; after several consonants in a row increases the probability of a vowel, etc.
We know that when combining dependent systems, the total entropy is less than the sum of the entropies of individual systems; therefore, the information transmitted by a segment of connected text is always less than one character multiplied by the number of characters. Taking into account this circumstance, a more economical code can be constructed if it is possible to encode not every letter separately, but whole “blocks” of letters. For example, in the Russian text it makes sense to encode in full some frequently occurring combinations of letters, such as “fucking up”, “ate”, “enactment”, etc. The coded blocks are arranged in decreasing order of frequencies, like the letters in the table. 18.8.1, and binary encoding is carried out according to the same principle.
In some cases, it turns out that it is reasonable to encode not even blocks of letters, but whole meaningful chunks of text. For example, to unload the telegraph on the holidays, it is advisable to encode whole standard texts with conditional numbers, like:
“Happy New Year, I wish you health and success in your work."
Without dwelling specifically on block coding methods, we confine ourselves to formulating the Shannon theorem relating to it.
Let there be a source of information 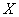 and receiver
and receiver 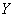 connected by communication channel
connected by communication channel 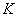 (fig. 18.8.1).
(fig. 18.8.1).
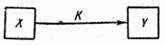
Fig. 18.8.1.
The source performance is known. 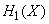 i.e., the average number of binary units of information coming from a source per unit of time (numerically, it is equal to the average entropy of the message produced by sources per unit of time). Let, besides, the known bandwidth
i.e., the average number of binary units of information coming from a source per unit of time (numerically, it is equal to the average entropy of the message produced by sources per unit of time). Let, besides, the known bandwidth 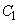 that is, the maximum amount of information (for example, binary characters 0 or 1) that a channel is capable of transmitting to the same unit of time. The question arises: what should be the bandwidth of the channel so that it “copes” with its task, i.e. that the information from the source
that is, the maximum amount of information (for example, binary characters 0 or 1) that a channel is capable of transmitting to the same unit of time. The question arises: what should be the bandwidth of the channel so that it “copes” with its task, i.e. that the information from the source 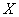 to receiver
to receiver 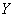 Received without delay?
Received without delay?
The answer to this question is given by the first theorem of Shannon. We formulate it here without proof.
1st theorem of Shannon
If the bandwidth of the communication channel is greater than the entropy of the information source per unit time
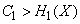 ,
,
you can always encode a sufficiently long message so that it is transmitted by the communication channel without delay. If, on the contrary,
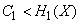 ,
,
then the transfer of information without delay is impossible
The Shannon-Fano algorithm is one of the first compression algorithms that was first formulated by American scientists Shannon and Robert Fano. This compression method is very similar to the Huffman algorithm, which appeared a few years later and is a logical continuation of the Shannon algorithm. The algorithm uses variable length codes: a frequently occurring symbol is encoded with a shorter code, rarely found with a longer code. The Shannon-Fano codes are prefix, that is, no codeword is a prefix of any other. This property allows you to uniquely decode any sequence of code words.
Shannon-Fano coding (eng. Shannon – Fano coding ) is an algorithm for prefix non-uniform coding. Refers to probabilistic methods of compression (more precisely, methods of context modeling of zero order). Like the Huffman algorithm, the Shannon-Fano algorithm uses message redundancy in a non-uniform frequency distribution of the characters of its (primary) alphabet, that is, replaces the codes of more frequent characters with short binary sequences and the codes of rarer characters with longer binary sequences.
The algorithm was independently developed by Shannon (publication “Mathematical Theory of Communication”, 1948) and, later, by Fano (published as a technical report).
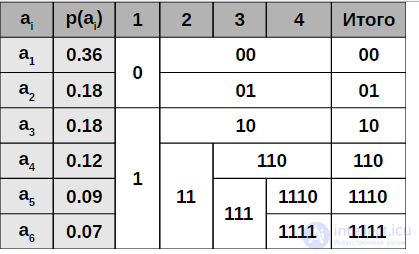
Example of building a code scheme for six symbols a1 - a6 and probabilities pi
When the size of the sub-alphabet becomes zero or one, the prefix code for the corresponding characters of the primary alphabet does not further extend, so the algorithm assigns prefix codes of different lengths to different characters. At the stage of division of the alphabet, there is an ambiguity, since the difference between the total probabilities p0-p1 can be the same for the two separation options (considering that all characters of the primary alphabet have a probability greater than zero).
The Shannon code - Fano is built using wood. The construction of this tree starts from the root. The entire set of encoded elements corresponds to the root of the tree (top of the first level). It is divided into two subsets with approximately the same total probabilities. These subsets correspond to two vertices of the second level, which are connected to the root. Then each of these subsets is divided into two subsets with approximately the same total probabilities.They correspond to the top of the third level. If the subset contains a single element, then it corresponds to the terminal vertex of the code tree; such a subset cannot be split. We proceed in this way until we get all the terminal vertices. Mark the branches of the code tree with symbols 1 and 0, as in the case of a Huffman code.
When constructing the Shannon-Fano code, the splitting of the set of elements can be done, generally speaking, in several ways. Choosing a partition at the level n can worsen the partitioning options at the next level (n + 1) and lead to non-optimal code as a whole. In other words, the optimal behavior at each step of the path does not guarantee the optimality of the entire set of actions. Therefore, the Shannon-Fano code is not optimal in a general sense, although it gives optimal results with some probability distributions. For the same probability distribution, in general, several Shannon-Fano codes can be constructed, and all of them can give different results. If we construct all possible Shannon-Fano codes for a given probability distribution, then among them will be all the Huffman codes, that is, the optimal codes.
Исходные символы:
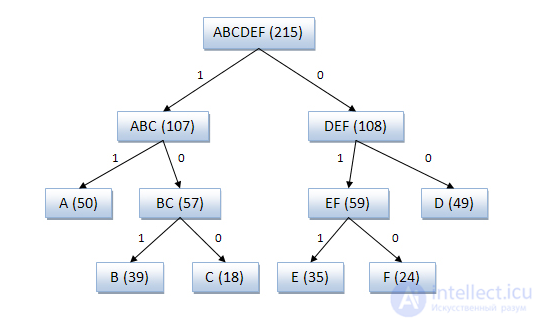
Кодовое дерево
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона — Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона — Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory