Lecture
13 1 Description of the LZW compression algorithm.
The LZW compression method uses the initial dictionary of ALL the various characters of the text being encoded. It can be built by analyzing the entire text. But more often, a ready-made and well-known standard ASCII + character label is used as the initial dictionary.
The compression process is as follows.
-Consistently read the characters in the input sequence and check whether there is such a line in the created string table (in the dictionary).
-If such a string exists, the next character is read,
-a if the string does not exist, then the code for the previous found string is entered into the output sequence , the string itself is entered into the dictionary table, and the search begins with the current character.
For example, if byte data (text) is compressed, then the rows in the initial table (ASCII +) dictionary will be 256 (from “0” to “255”). If a 10-bit code is used, then for codes for new lines, values remain in the range from 256 to 1023. New lines form a table sequentially, i.e., the row index can be considered its code.
The input decoding algorithm requires only encoded text, since it can recreate the corresponding conversion table directly from the encoded text. The decoding algorithm generates a uniquely decoded code due to the fact that every time a new code is generated, a new line is also added to the initial string table (in the dictionary). LZW constantly checks if the string is already known in the dictionary, and, if so, prints the existing code for this substring. Thus, each line will be stored in a single copy and have its own unique number. Consequently, when a message is restored, when a new code is received, a new line is added to the dictionary being restored, and when a new one is received, the line is extracted from the dictionary.
In general, according to the description of the compression process, the operation of the algorithm is not very easy, therefore, we consider an example of compressing and decoding a message.
Example 13.1 Compress text "abacabadabacabae"
First, create an initial dictionary of single characters. There are 256 different characters in standard ASCII, so the initial code size for encoding one character will be 8 bits. If we know in advance that there will be a smaller number of different characters in the source file, it is quite reasonable to reduce the number of bits to encode a character.
To initialize the table, we set the correspondence of code 0 to the corresponding character with byte 00000000, then 1 corresponds to the character with byte 00000001, 7 corresponds to 00000111, etc., up to code 255.
As the dictionary grows, the size of the groups must grow in order to accommodate new elements. 8-bit groups give 256 possible combinations of bits, so when the 256th word appears in the dictionary, the algorithm should go to 9-bit groups. When the 512th word appears, a transition to 10-bit groups will occur, which makes it possible to memorize already 1024 words, etc.
In our example, the algorithm knows in advance that only 5 different characters will be used , therefore, the minimum number of bits will be used to store them, allowing us to remember them, that is, 3pcs. (8 different combinations).
Coding
So let us compress the sequence "abacabadabacabae".
· Step 1: Then, according to the algorithm outlined above, we will add the “a” line to the initially empty line and check if there is a line “a” in the table. Since during initialization we entered into the table all the rows of one character, the string “a” is in the table.
· Step 2: Next, we read the next “b” from the input stream and check if there is a string “ab” in the table. There is no such line in the table yet.
· Add to table <5> “ab”. Output: <0>;
· Step 3: “ba” is not. In the dictionary: <6> “ba”. To exit: <1>;
· Step 4: “ac” is not. In the dictionary: <7> “ac”. Output: <0>;
· Step 5: “ca” is not. In the dictionary: <8> “ca”. To exit: <2>;
· Step 6: “ab” is in the dictionary; “Aba” is not. In the dictionary: <9> “aba”. To exit: <5>;
· Step 7: “ad” is not. In the dictionary: <10> “ad”. Output: <0>;
· Step 8: “da” - no. In the dictionary: <11> “da”. To exit: <3>;
· Step 9: “aba” is in the dictionary; “Abac” is not. In the dictionary: <12> “abac”. To exit: <9>;
· Step 10: “ca” is in the table; “Cab” is not. In the dictionary: <13> “cab”. To exit: <8>;
· Step 11: “ba” is in the table; “Bae” - no. In the dictionary: <14> “bae”. To exit: <6>;
· Step 12: And finally, the last line is “e”, followed by the end of the message, so we just output <4>.
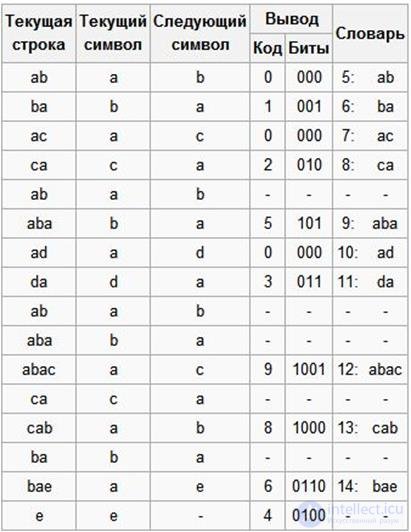
So, we get the coded message “0 1 0 2 5 0 3 9 8 6 4”, which is 11 bits shorter. In addition, for decryption, it is necessary to additionally store the initial dictionary: 0-a, 1-b, 2-c, 3-d, 4-e.
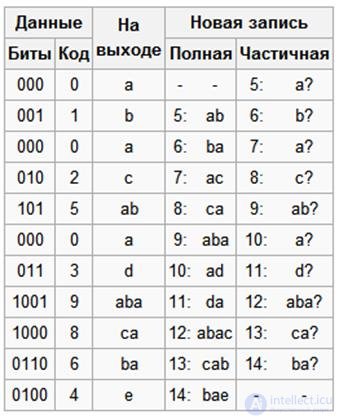
LZW decoding
A feature of the LZW algorithm is that for decompression, we do not need to save the entire table of rows to a file for unpacking. The algorithm is constructed in such a way that we are able to restore the table of rows using only the existing compressed sequence and the initial dictionary, or ASCII table.
Now imagine that we got the encoded message above, and we need to decode it. First of all, we need to know the initial vocabulary, and we can reconstruct the subsequent entries of the dictionary already on the move, since they are simply a union-union of the previous entries.
So decoding.
Advantages and disadvantages of LZW
Virtues
- Does not require calculation of probabilities of occurrence of characters or codes.
- For decompression, it is not necessary to keep the string table in the compressed file. The algorithm is constructed in such a way that we are able to restore the table of rows using only compressed code.
- This type of compression does not distort the source file, and is suitable for compressing data of any type.
H residue
The algorithm does not analyze the input data is therefore not optimal.
13 2 Application of LZ - data packaging algorithms .
The publication of the LZW algorithm made a big impression on all information compression specialists. This was followed by the development of a large number of programs and applications with different variants of this method.
This method allows you to achieve one of the best compression ratios among other existing methods of compressing image data, with no losses or distortions in the source files. Currently, it is widely used in TIFF, PDF, GIF, PostScript, and other files, as well as partly in many popular data compression programs (ZIP, ARJ, LHA).
If the LZ-type algorithm codes are transmitted for encoding the (adaptive) Huffman algorithm, then the resulting two-step (pipeline, rather than two-pass) algorithm will produce compression results similar to the well-known programs: GZIP, ARJ, PKZIP,
The highest compression ratio is given by two-pass algorithms, which source data sequentially compress two times, but they work up to two times slower than single-pass ones with a slight increase in the compression ratio.
Most archiving programs compress each file separately, but some compress files in the general stream, which gives an increase in the compression ratio, but at the same time complicates the ways of working with the resulting archive,. An example of a program that has the ability to compress files in a common stream is RAR. Unix OS archivers (gzip, bzip2, ...) almost always compress files in the general stream.
The format of the file containing the data that must be unpacked by the corresponding program by the archiver before use can, as a rule, be identified by the file name extension.
The following table lists some typical extensions and their corresponding archiver programs and data compression methods.
Table 13.1

Almost all file formats for storing graphic information use data compression. The format of the graphic file is also usually identified by the file name extension.
13 3 Test questions .
1. Why is the LZW encoding method shorter than the LZ77 or LZ78 methods?
2. Is it possible to decode an LZW code without exact knowledge of the initial dictionary of the original message?
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory