The main types of entropyedi are secret sources. Conditional and mutual entropy

Topic 2 . The main types of entropyedi are secret sources. Conditional and mutual entropy .

Lecture 2 .

2 1 Conditional entropy .

For further presentation, we need some known information from the theory of probability.

1) Properties of probabilities for an ensemble of random events A and B :

P (A, B) = P (A) * P (B / A); -> P (B / A) = P (A, B) / P (B);

P (A, B) = P (B) * P (B / A); -> P (A / B) = P (A, B) / P (A);

P (A / B) = P (A) * P (B / A) / P (B); P (B / A) = P (B) * P (A / B) / P (A);

If A and B are independent, then

P (A / B) = P (A); P (B / A) = P (B):

P (A, B) = P (A) * P (B);

Once again, the definition of entropy by Shannon for a source of discrete messages:

_{<! [if! vml]> 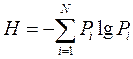<! [endif]>}

Properties:

H> 0 ;

Hmax = log N ;

With independent sources, H (A, B) = H (A) + H (B) ;

CONDITIONAL ENTROPY

If the states of the system elements are independent of each other, or if the state of one system does not depend on the state of another system, then the uncertainty that a certain element of the system (or some system) will be in one of the possible states would be completely determined by the probabilistic characteristics of individual system elements. In this case, the specific amount of information on the state of a system element or on one character of messages is called mean entropy, and when calculating it, the expression

_{<! [if! vml]> 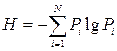<! [endif]>}

When calculating the average amount of information per message symbol, the interdependence is taken into account in terms of the conditional probabilities of the occurrence of some events relative to others, and the entropy obtained in this case is called conditional entropy .

Consider the transmission of messages from the source of random symbols A through an information transfer channel. With this, it is assumed that with reliable transmission when transmitting the character a ₁ we get b ₁ , a ₂ - b ₂ , etc. At the same time, for a channel with interference, the transmission is distorted, and upon receipt of the symbol b ₁ we can only talk about the probability of transmitting the symbol a ₁ . It may well be that the characters a ₂ , a ₃ , etc. were transmitted.

Distortions are described by the matrix of conditional probabilities of the channel P (A / B) = {p (a _i / b _i } , as shown in Fig. 2.1

<! [if! vml]> 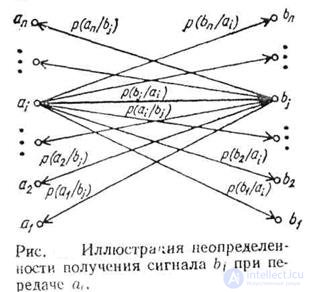<! [endif]>

Fig. 2.1

Consider the process of transmitting signals over a communication channel with interference and use it to understand the mechanism for calculating the conditional entropy.

If the message source displays characters

a _l , and ₂ , ..., a _i ..., and _n

with probabilities, respectively

p (a ₁ ), p (a ₂ ) ..., p (a _i ), ..., p (a _n ),

and at the output of the transmission channel we get the characters

b ₁ , b ₂ , ..., b _i ..., b _n

with probabilities, respectively

p (b ₁ ), p (b ₂ ), ..., p (b _i , ..., p (b _n ),

then the concept of conditional entropy H (B / a _i ) expresses the uncertainty that, by sending a _i , we get b _i ., the concept H (A / b _i ) the uncertainty that remains after receiving b _i that it was sent a _i . Graphically, this is shown in the above figure. If interference is present in the communication channel, then with a different degree of probability any of the signals b _j can be received and, conversely, the received signal b _j can appear as a result of sending any of the signals a _i . If there is no interference in the communication channel, then always the sent symbol а ₁ corresponds to the received symbol b ₁ , and ₂ - b ₂ , ..., and _n - b _n .

In this case, the entropy of the source of messages H (A) is equal to the entropy of the receiver of messages H (B) . If interference is present in the communication channel, then they destroy or distort part of the transmitted information.

Information losses are completely described through private and general conditional entropy. The calculation of the partial and total conditional entropy is conveniently performed using channel matrices. The term “channel matrix”, meaning: a matrix that statistically describes a given communication channel, is used for brevity. If the communication channel is described from the side of the message source (i.e., the signal sent is known), then the probability that when transmitting the signal a _i over the communication channel with interference, we get the signal b _j denoted as the conditional probability p (b _j / a _i ) . and the channel matrix has the form

<! [if! vml]> 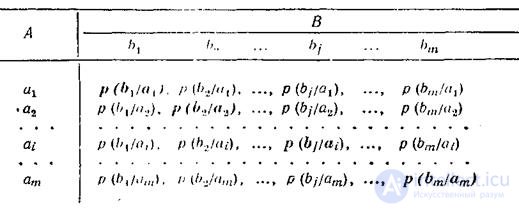<! [endif]>

The probabilities, which are located diagonally (in bold), determine the probabilities of correct reception, the rest - false. The values ​​of the digits that fill the channel matrix columns usually decrease with distance from the main diagonal and, in the absence of interference, everything except the numbers located on the main diagonal is equal to zero.

The passage of the character a _i from the source of messages in a given communication channel is described by the distribution of conditional probabilities of the form p (b _j / a _i ), the sum of the probabilities of which must always be equal to one. For example, for signal a ₁

<! [if! vml]> 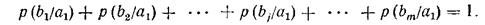<! [endif]>

Information losses attributable to the signal fraction a _i are described using partial conditional entropy. For example, for signal a ₁

<! [if! vml]> 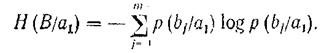<! [endif]>

The summation is performed on j, since the i -th state (in this case, the first) remains constant.

The losses in the transmission of all signals over a given communication channel are described using the general conditional entropy. To calculate it, all partial conditional entropies should be summed, that is, double summation over i and j should be performed .

In case of uneven appearance of the character of the message source, one should take into account the probability of each symbol appearing, multiplying the corresponding partial conditional entropy. At this, the general conditional entropy

<! [if! vml]> 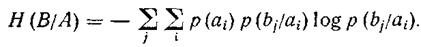<! [endif]>

If we examine the situation on the part of the receiver of messages (that is, when the received signal is known ), then with the receipt of the symbol b _j it is assumed that some of the symbols a ₁ , a ₂ , ..., a _i , ..., a _m were sent. In this case, the channel matrix has the form:

<! [if! vml]> 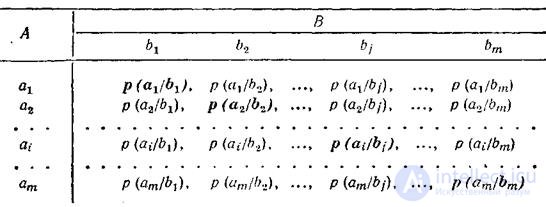<! [endif]>

In this case, the unit should be equal to the sum of conditional probabilities not by rows, but by the columns of the channel matrix

<! [if! vml]> 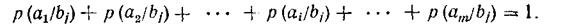<! [endif]>

Partial conditional entropy

<! [if! vml]> 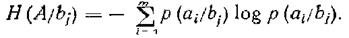<! [endif]>

And total conditional entropy

<! [if! vml]> 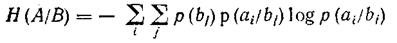<! [endif]>

The total conditional entropy of system B relative to system A characterizes the amount of information contained in any symbol of the source of messages, through which we present the states of the elements of the systems under study.

The total conditional entropy is determined by averaging over all symbols, i.e., over all states a _i , taking into account the probability of occurrence of each of them. It is equal to the sum of the products of the probabilities of the appearance of source symbols for uncertainty, which remains after the addressee has accepted the symbols:

<! [if! vml]> 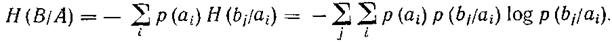<! [endif]>

If there are no interferences in the communication channel, then all elements of the channel matrix, except those located on the main diagonal, are equal to zero. This suggests that when transmitting the signal a _1, we will certainly get b ₁ when transmitting a ₂ -b ₂ , ..., and _m - b _m . The probability of obtaining the correct signal will become unconditional , and the conditional entropy will be zero .

The maximum entropy reaches its maximum in the case when, by transmitting the symbol a _{i, it} can be equally likely to get any of the signals b ₁ , b ₂ , ..., b _m .

2 2 Basic properties of conditional entropy .

Property 1 . If the ensembles of messages A and B are mutually independent, then conditional entropy A relative to B is equal to unconditional entropy A , and vice versa conditional entropy B relative to A is equal to unconditional entropy B

<! [if! vml]> 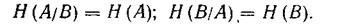<! [endif]>

Evidence. If messages A and B are mutually independent, then the conditional probabilities of individual characters are equal to unconditional:

<! [if! vml]> 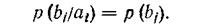<! [endif]>

Since p (a _i ) * p (b _j / a _i ) = p (a _i , b _j ), the expression for H (B / A) can be represented as:

<! [if! vml]> 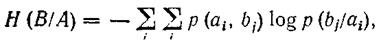<! [endif]>

substituting in the resulting expression

<! [if! vml]> 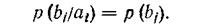<! [endif]>

will get

<! [if! vml]> 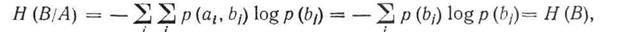<! [endif]>

because

<! [if! vml]> 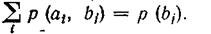<! [endif]>

Property 2: If the ensembles of messages A and B are so strictly statistically related that the appearance of one of them necessarily implies the appearance of the other, then their conditional entropies are zero:

<! [if! vml]> 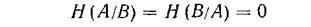<! [endif]>

Proof. Using the properties of probabilities, according to which, with the full statistical dependence p (b _j / a _i ) = 1 , the terms p (b _j / a _i ) * log (p (b _j / a _i ) in the expression for entropy are also zero. If the individual terms are equal to zero, and the sum is zero, whence

<! [if! vml]> 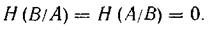<! [endif]>

Findings:

1. The entropy of the message, made with regard to the unevenness of the characters is less than the entropy of the message, composed of equiprobable characters.

2. The entropy of a message, made up of the interdependence of characters, is less than the entropy of the same message, made up of independent characters.

3. The maximum entropy has messages composed of equiprobable and independent characters, i.e., those in which the conditional entropy is equal to and the probability of occurrence of alphabet characters is p _i = 1 / N.

2.3 Mutual entropy. Entropy properties of union.

The entropy of the union or mutual entropy is used to calculate the entropy of the joint appearance of statistically dependent messages or the entropy of interconnected systems.

For example, when transmitting via a communication channel with the noise of the digit 5, out of 100 times the digit 5 ​​was accepted 90 times, the digit 6 — eight times, the digit 4 — twice. The uncertainty of the occurrence of combinations of the type 5-4; 5-5; 5–6 before transferring the number 5 can be described using the entropy of the union H (A, B).

Understanding the entropy of the union (sometimes use the term "mutual entropy") is facilitated if the reasoning is reduced to some conditional communication channel. Using the example of information transmission via a communication channel, it is also more convenient to trace the relationship between the concepts of conditional entropy H (B / A) and mutual entropy H (A, B).

So, let (a ₁ , a ₂ , ..., a _i .... a _n ) be a sample space A, or characters characterizing the source of messages, a (b _1, b ₂ , ..., b _j , ..., b _m ) selective space B, or characters characterizing the receiver of messages. In this case, a is a signal at the input of a noisy drip, and b is a signal at its output. The relationship of the transmitted and received signals is described by the probabilities of joint events of the form p (a, b), and the relationship of sample spaces A and B is described by a matrix of the form:

<! [if! vml]> 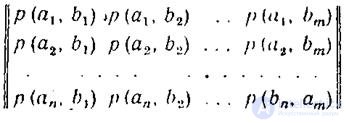<! [endif]>

If the matrix describes a communication channel, then the number of rows of the matrix is ​​equal to the number of columns m = n and the limits of summation over i and j are the same. When describing the interaction of systems, the equality m = n is optional.

Regardless of the equality or inequality of the number of rows to the number of columns, the unification matrix has the property:

<! [if! vml]> 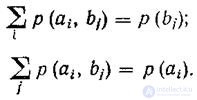<! [endif]>

In turn,

<! [if! vml]> 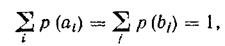<! [endif]>

i.e.

<! [if! vml]> 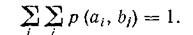<! [endif]>

This property allows you to calculate the entropy of the source and receiver of messages directly on the union matrix:

<! [if! vml]> 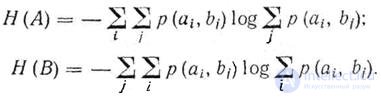<! [endif]>

Before the sign of the logarithm, summation is performed over i and j , since to find unconditional probabilities, it is necessary to perform summation over one coordinate (meaning the matrix representation of probabilities), and to find the corresponding entropy, summation is done along another coordinate.

Conditional probabilities' using the union matrix are as follows:

<! [if! vml]> 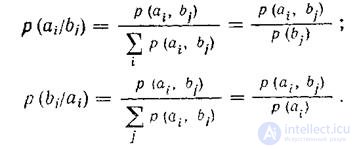<! [endif]>

<! [if! vml]>

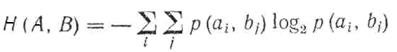<! [endif]>
The entropy of combining ensembles A and B with the help of the combining matrix is ​​calculated by successively summing over the rows or go columns of all probabilities of the form p (a, b) multiplied by the logarithm of the same probabilities

The dimension of this entropy is “bits / two characters”

The dimension of “bits / two characters” is explained by the fact that the reciprocal entropy represents the uncertainty of the occurrence of a pair of characters, i.e. uncertainty by two characters. If there is no dependence between the two characters, the expression for H (A, B) takes the form of the expression H (A) or H (B) , and accordingly the dimension will be “bit / symbol”.

Investigate expressions for mutual entropy

From the theory of probabilities it is known that (we look at the basic relations at the beginning of the lecture)

<! [if! vml]> 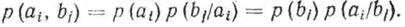<! [endif]>

Using this property, the expression for mutual entropy can be written as

<! [if! vml]> <! [endif]>

But

<! [if! vml]> <! [endif]>

and,

<! [if! vml]> <! [endif]>

then the first term of the expression takes the form

<! [if! vml]> <! [endif]>

The second term is none other than H (B / A), which allows the expression to be written as

<! [if! vml]> 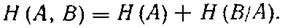<! [endif]>

The entropy of the union of the transmitted ensemble A and the received ensemble B is equal to the sum of the unconditional entropy H (A) and the conditional entropy H (B / A).

The latter in this case represents the additional information that the message gives after the information contained in message A became known. Thus, conditional entropy represents the uncertainty that a b was sent at reception b , and mutual entropy reflects the uncertainty of the pair ab type.

Union entropy has a symmetry property.

H (A, B) = H (B, A)

The symmetry property of the entropy of a union is well illustrated by the matrix shown in Figure 2.2.

<! [if! vml]> 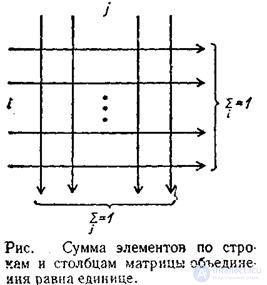<! [endif]>

Fig. 2.2

Indeed, if we sum up all the elements of the union matrix in rows and columns according to the figure scheme and then add the results, then both sums will be equal to one. The symmetry property allows you to write the relationship between the conditional entropy and the entropy of the union as follows:

<! [if! vml]> 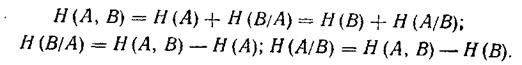<! [endif]>

If a probability matrix p (a, b) is constructed , describing the relationship of two arbitrary sample spaces, in particular, the relationship between the input and output of a noisy communication channel, the other informational characteristics may not be specified, since the mutual entropy matrix has information completeness.

Mutual information between the ensemble of messages of source A and receiver B is expressed by the formulas

<! [if! vml]> 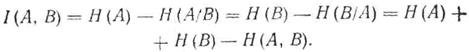<! [endif]>

<! [if! vml]> 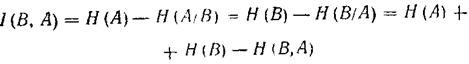<! [endif]>

In the absence of statistical dependency between the elements of the A and B ensembles, the conditional probabilities turn into unconditional

<! [if! vml]> 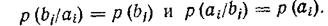<! [endif]>

In this case

<! [if! vml]> 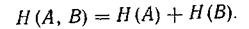<! [endif]>

With a complete statistical dependence between the elements of the ensembles A and B (for example, when the result of one event uniquely identifies information about another event)

H (B / A) = H (A / B) = 0,

and mutual entropy

<! [if! vml]> 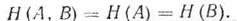<! [endif]>

In the case of transmission of information via communication channels, the full statistical dependence between the transmitted and received signals indicates the absence of interference, the channel matrix acquires the form

<! [if! vml]> <! [endif]>

the conditional probabilities of correct reception are equal to unity, the rest are zero, which makes all partial conditional entropies vanish.

<! [if! vml]> <! [endif]>

similarly

<! [if! vml]> <! [endif]>

and, therefore, the total conditional entropy turns into zero and the expression for H (A, B) takes the form

<! [if! vml]> <! [endif]>

Findings:

1. The entropy of the combined system A, B is equal to the unconditional entropy of one of them plus the conditional entropy of the second relative to the first.

2. The “association” matrix, which describes the interaction of systems or ensembles of messages using probabilities of joint events, has the property of informational completeness (and the sum of its elements is equal to 1).

3. Mutual entropy of ensembles of arbitrary sample spaces has the property of mutual symmetry.

4. In the case of statistical independence of elements of ensembles, the mutual entropy of any number of ensembles is equal to the sum of their unconditional entropies.

5. With a complete statistical dependence of the ensemble of the source of messages and the ensemble of the receiver of messages, their mutual entropy is equal to the unconditional entropy of the source of messages.

2.4 Test questions.

1. What is the basic meaning of the concept of conditional entropy.

2. Give the concept of a channel channel matrix with interference.

3. List the basic properties of conditional entropy.

4. Name the basic mutual entropy.

5. What more fully defines the channel of information transfer: conditional or mutual entropy?