Lecture
The concept of a cellular automaton is not new. It is described in
many books [1, 9] and, moreover, there are people who have dedicated cellular
machines all my life [2].
The history of cellular automata begins more than half a century ago. Many
the books indicate that the cellular automaton is the result of the work of John Von
Neman (John von Neumann) and Konrad Zuse (Konrad Zuse), who at the beginning
Forties of the 20th century developed into the idea of a universal computing
environments for building, analyzing and comparing the characteristics of algorithms [10].
The works of these scientists are based on the research of Stanislav Ulam
(Stanislaw Ulam) [11].
To date, cellular automata have found wide
distribution in all spheres of human activity: mathematics,
physics, biology [12], chemistry, mechanics, cryptography [13], hydrodynamics,
gas dynamics [14, 15], etc. The main application of cellular
automata is the simulation of dynamic processes for example
movement of the crowd [16] or the distribution of heat flow [17]. Some
scientists believe that cellular automata is the principle on which
nature acts in everyday life. The most detailed about this
described in Stephen Wolfram’s book “A New Kind of
Science ”[2].
The principle of cellular automata is based on local interactions.
All elements in any considered system act on the same
to the principles. Taken together, the results of the work of simple rules on which
based interactions, allow you to get complex behavior. John
von Neumann gives the following definition of cellular automata: “Cellular
automata are discrete dynamical systems, the behavior
which is completely defined in terms of local dependencies. AT
to a large extent also the case for a large class of continuous
dynamical systems defined by partial differential equations. AT
In this sense, cellular automata in computer science are analogous to
of the physical concept of "field" ... a cellular automaton can be thought of as
stylized world. The space is represented by a uniform grid, each
a cell or cell which contains several data bits; time runs
forward in discrete steps, and the laws of the world are expressed only
a set of rules, say, a small reference table, according to which any
the cell at each step calculates its new state by its states
close neighbors. Thus, the laws of the system are local and
everywhere the same. “Local” means that in order to learn,
what happens here a moment later, just look at the state
Neighborhood environment: no long range is allowed.
“Equality” means that the laws are the same everywhere: I can distinguish
one place from another only in the form of the landscape, and not for some difference
in the laws "[1
Formally, a cellular automaton can be defined as a set of {G, Z, N, f},
where G is the metric of the field on which the cellular automaton acts;
Z is the set of states of each cell;
N is a neighborhood of a cell that affects the state of a given cell;
f - rules of the cellular automaton, which in the mathematical form can
be written z x z ^ | n | -> Z.
The properties of the cellular automaton are: the locality of the rules,
homogeneity of the system, the finiteness of many states of the cell,
simultaneous changes for all cells. In more detail and formally
The basic properties of the classic cellular automaton are given in
[18].
Cellular automata can work in several dimensions: it can
process cell state vector, plane or three-dimensional model.
In all cases, to visualize the operation of the machine often add
additional dimension - time that allows you to evaluate changes
field states in dynamics.
The most famous cellular automata application can be considered
the game “The Life” of John Conway [10, 19].
There are several types of cellular automata. Below
their main types are listed from Stephen Wolfram’s book “A New Kind of
Science ”[2].
Standard cellular automata based on the classic definition.
Cells of the field of such an automaton change state depending on
states of neighboring cells, and thus the field changes its state.
Examples of standard one-dimensional cellular automata are presented in
rice one.


Fig. 1. Cell structures created using standard
cellular automata
Fig. 2. Cell structure created using mobile
cellular automaton
Mobile cellular automata are similar to standard cellular
automata have cell states that change over
time, but unlike them, one active is additionally defined
cell. Only an active cell changes state at each moment.
of time. An example of cellular structure generated by mobile cellular
as shown in fig. 2
Turing machines like a mobile cellular automaton
has only one active cell. Additional condition - definition
several states of the active cell, as shown in Fig. 3
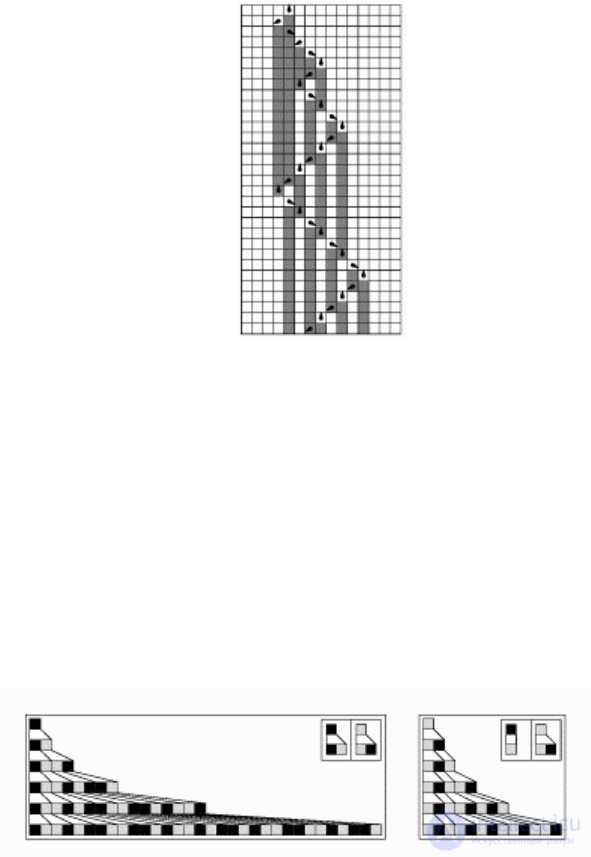
Fig. 3. The cellular structure created by the cellular
automatic turing machine
Fig. 4. Cell structure created using the substitution system
The substitution system is a cellular automaton, which at each step
replaces a cell with a block of other cells. An example of the machine is shown in
rice four
Sequential substitution systems scan
a sequence of points for compliance with the conditions of each rule, with
satisfying the rule, substitution occurs and scanning begins
again, as shown in fig. five

Fig. 6. Cell structure created with tag system
Rules that remove elements from the beginning of a chain of cells and
other cells are added to the end of the chains, called tag systems.
An example is shown in Fig. 6
The cyclical tag system can be achieved by alternating
use of different systems of rules. As a result, the nature of behavior
cellular automaton becomes specific, as can be seen in Fig. 7
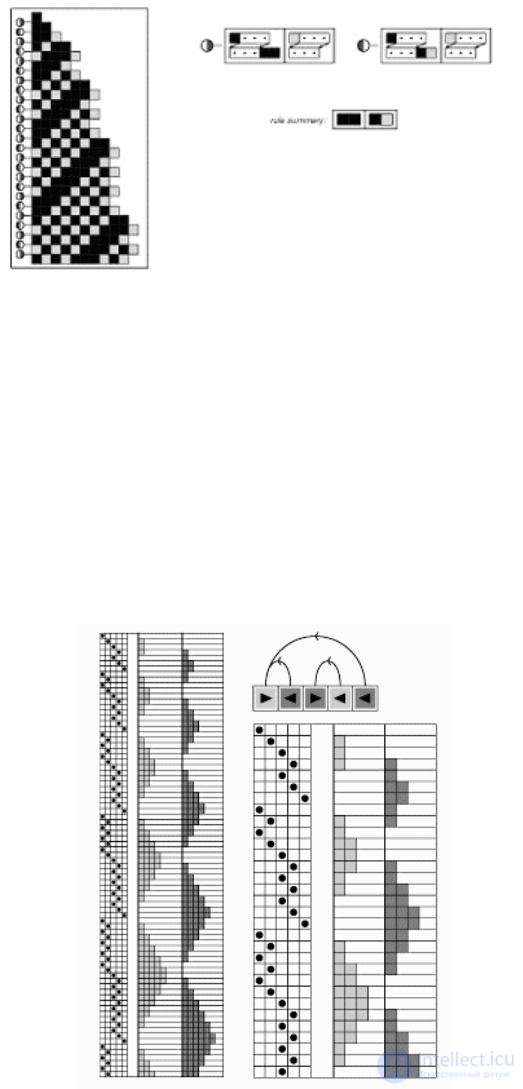
Fig. 7. Structure created using cyclic tag system
Fig. 8. Structure created using the register machine
Register machines perform a given program. If successful
When a program element is executed, a specified transition occurs, otherwise
transition to the next item. An example is shown in Fig. eight.
In a symbolic system at each step, each region is enclosed in
brackets, transformed by the given rules. As a result
a sequence is formed. An example is shown in Fig. 9

Fig. 9. Structure created using the character system
The concept of a cellular automaton with labels introduced by the author of this
work. The reason for its creation was the need to achieve
specified characteristics of cellular automata in the development of algorithms
text recognition process. As will be shown later, this concept
allows you to effectively implement feature extraction algorithms
characters.
In the process of working on dissertation - analysis of the literature - found
the concept of memory in the theory of turing machines [20]. It determines that
the head of the turing machine can store some finite number
data that is used by machine rules to change
tape machine or movement of its head. This concept when introducing
some restrictions and the transition to the theory of cellular automata may
also be reduced to tagged cellular automata.
The principle of the cell system with labels is the association
each cell of the field with one or more labels.
An example of a cellular automaton with labels is the set: field,
on which only cells of black and white colors are identified, a label,
which may or may not be present in the cells of the field, and the rules
taking into account the presence of labels in neighboring cells. In the case of determining one
labels for cellular automata, the number of states of each cell
doubled in the case of no tags. In the above
In the example, the number of states of each cell is four. Rule
cellular automaton in such a system will look like
in fig. ten.
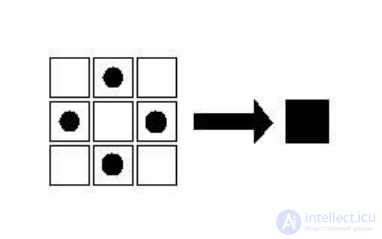
Fig. 10. Example of a cellular automaton rule with tags
This example uses a rule based on eight neighbors.
Without labels, the number of variants of such rules (if
only two colors of cells) will be 2 ^ 10 = 1024 (nine cells of conditions and one -
result). Adding a label will result in (2 · 2) ^ 10 = 1024 ^ 2 = 1 048 576
options for the rules. It is more convenient, in this case, to separate the colon
numbering colors and labels. Then for the rule shown in the figure
10, the number can be 1: 340 (or in binary
0000000001: 0101010100, where each digit determines the state of the cell,
the cells are numbered from left to right from top to bottom), where the first number identifies
the color conversion rule, and the second number is the label change rule.
The rule for the field on which more than one label is defined,
numbered in the same way: for a rule with two labels, x: y: z,
where the first number defines the color conversion rule, the second number -
conversion of one label, the third number - the second label.
Cellular tagged machine allows for complex results
without changing the structure of the cell system being used. For example, for
given image, this machine allows you to define some
properties of this image and highlight its characteristic features without
color changes.
Formal description
The cellular automaton with labels is a set of {G, M, Z, N, f}. Description
each item is presented below.
1. G is a finite discrete metric set that guarantees
finite distance between cells.
2. M is a finite set of labels defined for each cell.
3. Z is the final set of cell states.
4. N is a finite set that defines the neighborhood of a cell as follows.
the way that each element of the set allows you to define a neighbor for
every cell. | N | - the number of neighboring cells that affect
condition given.
5. f - cellular automaton rules corresponding to the mathematical
transition functions:
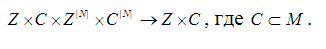
Below it is shown that the cellular automat with tags satisfies
requirements of the classic cellular automaton.
By definition, a cellular automaton is given by four elements {G *,
Z *, N *, f *} [18]. Elements G and N of cellular automata with labels
correspond to the classical elements G * and N *.
We introduce Z ^ = Z x C in such a way that | Z ^ | = | Z | x | C |. Set Z ^
will correspond to the Z * classical definition of a cellular automaton,
since it is finite and determines all variants of cell states
automat.
Similarly, f ^ = (Z ^ x Z ^) ^ | N | -> Z ^ will correspond to f *, since
All states on the first and second time layer are taken into account.
Thus, the set {G, Z ^, N, f ^} of the cellular automaton is obtained,
which all properties are fulfilled: rules locality (provided by N),
homogeneity of the system based on the metric G, finiteness of the set
cell states Z ^, simultaneous changes for all cells, guaranteed by the rule set f ^.
Consider an example of a cellular automaton labeled "chessboard."
The task of the “chessboard” machine is to draw
alternating black and white dots on white image.
To perform the task to the cellular machine labeled "chess
board "eight rules are enough: 0: 257, 0:65, 0: 321, 1:52, 513: 52, 256: 52,
64:52, 320: 52 (the unexamined states of the nine original cells are not
change the state of the resulting cell). These rules are depicted on
rice eleven
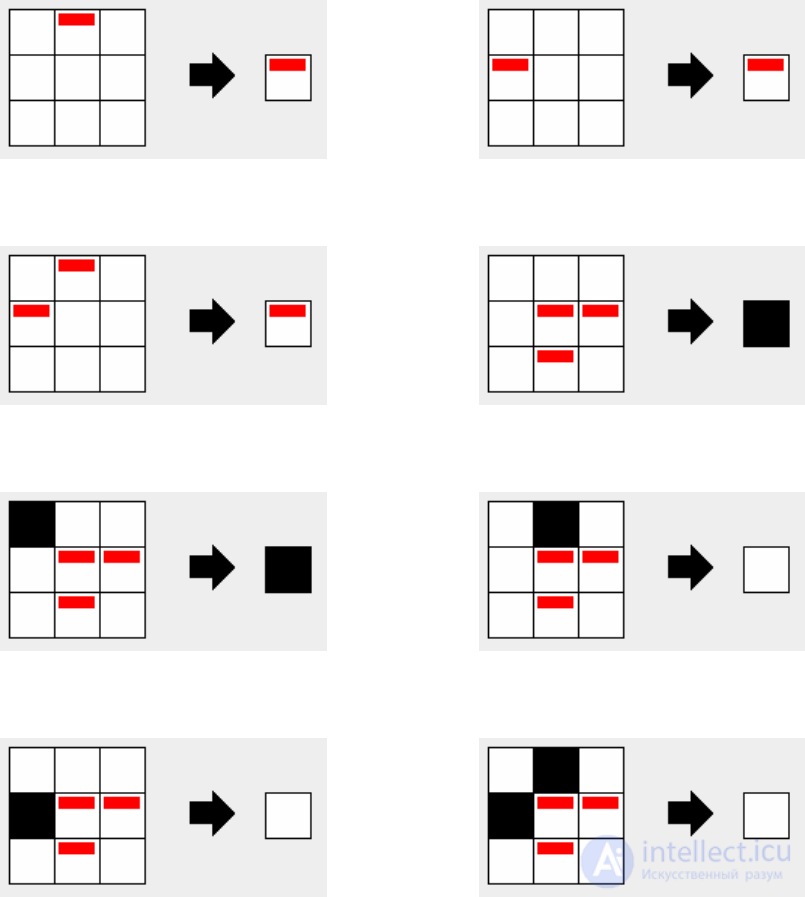
Fig. 11. Rules of the “chessboard” cellular automaton, rules:
a - 0: 257, b - 0:65, c - 0: 321, g - 1:52, d - 513: 52, e - 256: 52, f - 64:52,
s - 320: 52
To start the machine you need to put a label on the start
field point. The result of the operation of the machine at steps 1, 3, 5, 10, 20 is shown in
rice 12.

Fig. 12. The result of the work of the cellular automaton labeled "chess
board "on the steps: a - the first, b - the third, in the fifth, d - the tenth, d -
the twentieth
This example illustrates the use of cellular automata with
tagged, but does not affect the practical utility that you can
provide with their use: the ability to determine the characteristics,
without changing the color of the processed image.
The cellular automaton is a powerful tool for performing tasks.
modeling. Clearly identifying all its components (field metric,
cell conditions, number of neighbors affecting the cell and rules of operation
machine), you can solve a huge number of problems, many of which have not
trivial solutions [2].
Unfortunately, not all tasks that can be solved based on
cellular automata can be solved by using a small number of them.
Moreover, to solve a part of the tasks it may be necessary
a sequence of cellular automata, each of which decides
specialized task.
The sequence of cellular automata is a collection of cellular
automata, each of which is based on specific rules.
Cellular automata in the sequence start at a given
sequences and each regular cellular automaton begins
work on the field that was formed by the previous cellular
automat in sequence.
The sequence of automata will not necessarily complicate the logic.
system operation. In section 3.2 it will be shown that use
sequences of cellular automata helps to manage small
the number of rules for each cellular automaton when solving
nontrivial task
In the case of the use of cellular automata labeled in
cellular automata sequences need to be determined in advance
the same set of M possible labels of the cells of the field of each automaton. it
helps maintain consistency in working condition.
Comments
To leave a comment
System modeling
Terms: System modeling