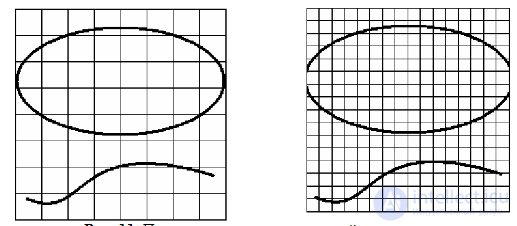
Fig. 11. Reducing cell size increases accuracy.
Summarizing these relations, we get:
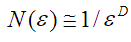 where D is the dimension
where D is the dimension the studied set. The dimension acts as a number characterizing
the growth rate of the number of cells covering this set with decreasing size
cells Next, we logarithm and direct ε to zero:
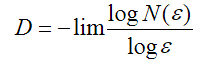
(3)
It is clear that the dimension of the line calculated by this formula will be equal to 1,
the dimension of the plane is 2, the dimension of the volume is 3. In general, the dimension
“Familiar” to us objects is expressed by an integer. But it turns out you can
construct such objects, the dimension of which will be fractional.
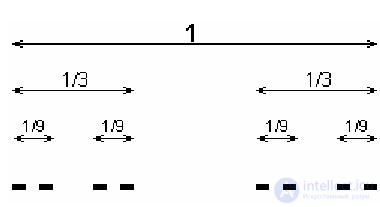
For example, examine the Cantor set, which is constructed as follows.
way: a single segment is divided into three equal parts and the middle part
ejected, then everything repeats for the remaining two parts, etc. Eventually
we have such a picture (Figure 12):
 where D is the dimension
where D is the dimension 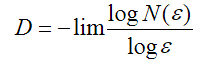 (3)
(3) 
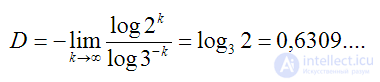
Comments
To leave a comment
System modeling
Terms: System modeling