Lecture
Quality assessment shows how theoretical calculations for the constructed model deviate from experimental data. The presence of a connection between two variables is called a correlation.
If quality assessment is applied before the study, then it solves the problem: is there a connection between input X and output Y and estimates the strength of this connection.
The linear correlation coefficient indicates whether there is a linear relationship between two rows X and Y and which force. Calculated by the following formula:
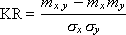
m x , m y , m xy - expected value x, y, xy:

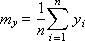
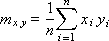
The dispersion of σ x 2 and σ y 2 shows how scattered the points are from the average value:
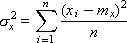
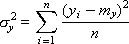
The linear correlation coefficient may have a plus or minus sign. Its positive value indicates a direct connection between X and Y. The closer KR is to +1, the closer the connection. A negative value indicates feedback; in this case, the limit is –1. The proximity of KR to zero indicates a weak connection between X and Y (see Fig. 9.1).
| |
| Fig. 9.1. |
| |
| Fig. 9.2. |
The non-linear correlation coefficient is calculated by the following formula:
bug09.05. Check all these formulas !!!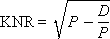
P - the spread between the real points and the average value: bug09.07. average value?
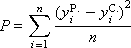
D - the spread between the hypothetical curve and real points:
?? 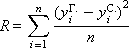
R - the spread between the hypothesis and the average value:
?? 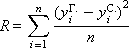
X and Y are represented as rows z i and u i in order to exclude the constant component: z i = x i - m x
u i = y i - m y
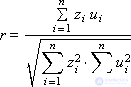
When r -> 1, there is a close correlation. When r -> 0, the processes are mutually orthogonal, there is no correlation, the processes are not related to each other.
bug09.09 Clearer pictures
The strength of the connection between the past and the present of a single process is investigated. To do this, the signal is compared with itself, shifted in time, and the correlation coefficient of two time series is calculated (see p. 3).
bug09.12. Unclear drawing
Whether there is a periodicity in the dynamic range can be determined by performing a direct Fourier transform and examining the spectrum of the signal under study. This is described in Lecture 07 “Model of a dynamic system in the form of a Fourier representation (signal model)”
| |
| Fig. 9.5. |
The coefficient of multiple correlation R:
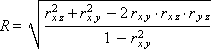
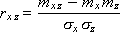
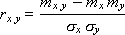

Formula
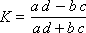
where K is the coefficient of associations, allows you to find out if there is any connection between the two signs. If this coefficient is close to unity, then in this case we can talk about the existence of such a connection.
Example. Let's try using this formula to find out whether there is a relationship between height and weight of a person? Suppose we have at our disposal data on the weight and height of 500 people:
| Table 9.1. | |||||||||
|
According to the formula: K = (304 · 67 - 17 · 112) / (304 · 67 + 17 · 112) = 0.83. Since the value of 0.83 is close to 1, then we can talk about the existence of a certain relationship between weight and height.
Comments
To leave a comment
System modeling
Terms: System modeling