five . State machines 5.1. Concept of automaton

Information converters around us do not always perform a purely functional display of information. The result of the input conversion  the output often depends not only on what information currently appears at the input, but also on what happened before, on the history of the conversion. Biological systems provide many examples of this. For example, one and the same entrance - a neighbor's apology after he stepped on your foot in a crowded tram - will cause you one reaction for the first time and a completely different one for the fifth time. Apparently, your reaction will depend on previous events that occurred in the tram, in other words, on the input history.

Thus, there are more complex, non-functional information transformers; their reaction depends not only on the input at the moment, but also on what was at the entrance earlier, on the input history. Such converters are called automatic.

If the number of different input elements of a given converter has a finite number (as in the final functional converter), then the number of possible input histories is finite (countable). If an automaton behaves differently for each possible prehistory, then such an automaton should have a memory in order to memorize all these prehistories. The corresponding formal model is called a finite automaton information converter, or simply a finite automaton .

We introduce an equivalence relation on the prehistory set. Two prehistories will be considered equivalent if they influence the further behavior of the automaton in the same way. It is obvious that for its functioning the automaton does not have to memorize the input histories, it is enough that it remembers only the equivalence class (for example, its number) to which the given history belongs. The equivalence class of its input histories is called the internal state of the automaton.

In its internal states, the automaton remembers its “concentrated past”. Informally, the state of the system is a characteristic that uniquely determines its further behavior, all subsequent system responses to external events. The finite state machine can react differently to the same input signal depending on the state it is in at the moment. Since the state is a class of equivalent prehistory of inputs, the state can change only with the arrival of the next input signal. Upon receipt of the input signal, the state machine not only provides information to the output as a function of this input signal and the current state, but also changes its state, as the input signal changes the prehistory. Based on the concept of formal grammars, we will assume that the input and output variables, as well as the internal states of the finite automaton, take values ​​from some finite alphabets. Let X be the alphabet of the input variable xi, Y the alphabet of the output variable yi, and Q the alphabet that defines the internal states of the automaton qi.

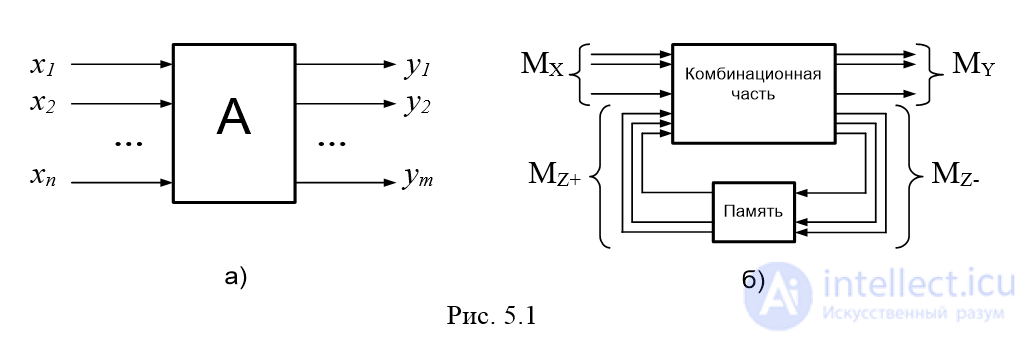
Fig. 5.1

The operation of the machine is conveniently represented graphically in the form of a flowchart. In this case, the structure of the finite automaton in the general case has the form of a certain multipole — a “black box” (Fig. 5.1a) —with a set of MX input vectors and a set of MY output vectors. The set of internal states of MQ is characterized by a memory that stores the input sequence (history) of the automaton. The enlarged internal structure of the finite state machine is shown in Fig. 5.1b. Here MZ- is the set of vectors characterizing the input feedback channels (memory); MZ + is a set of vectors characterizing the output feedback channels (memory). Moreover, each internal state of the automaton qi is characterized by a certain set of inputs xi and z + i. The number of internal states of the automaton is called the automaton memory capacity .

The models of finite automata considered in the course are abstract descriptions of control systems of technical automated devices or computational processes. The basis of these models is the assumption that these automata operate in a discrete way, i.e. input and output variables, as well as internal states are not continuous functions in time, but change at fixed times τ v ( v = 1,2, ...). It is assumed that a finite automaton can have only one of a finite set of internal states qi. This state remains unchanged in the time interval between τ v and τ v +1 , which we will further call the cycle cycle . The duration of a cycle is not necessarily a constant value, and the transition of the automaton from one internal state to another depends only on the sequence number of the cycle v i . At the same time, the state of the finite state machine at any clock moment τ v is characterized by a set of input variables at a given clock point and the internal state of the machine at the previous clock moment τ v -1 .

Having considered the basic concepts and terms, you can give a precise definition of a finite state machine. A finite automaton is an ordered five of objects A = {X, Y, Q, δ, λ}, where:

X is the final non-empty set of input signals (input alphabet);

Y is the final non-empty set of output signals (output alphabet);

Q is a finite nonempty set of internal states;

δ is the transition function (map Q × X → Q);

λ is the output function (Q × X → Y mapping).

Thus, in the definition of an automaton, there are three finite sets X, Y, Q and two functions δ and λ, defining some relations between the elements of these sets. The power sets X, Y, Q are equal respectively:

| X | = 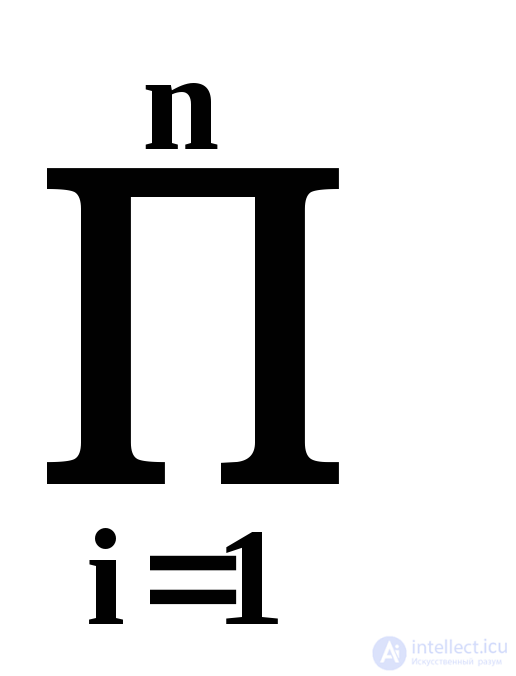p i ; | Y | = 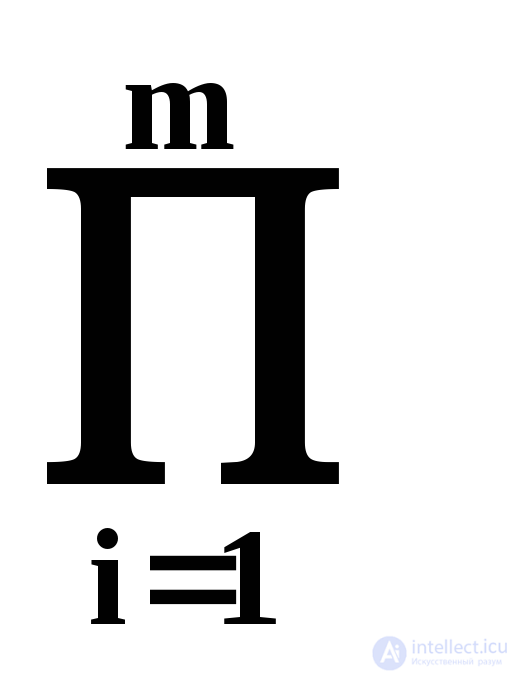r i ; | Q | = 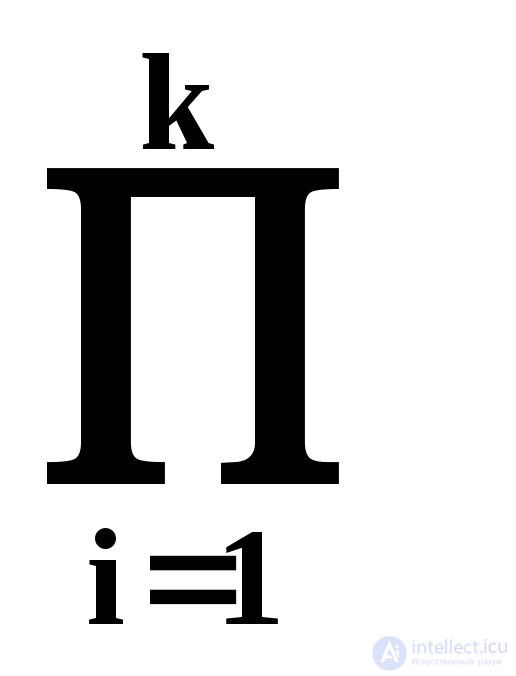s i ,

where p i , r i and s i - the number of characters in the alphabets of the input variable x i , the output variable y i and state variable q i . With the binary structure of all alphabets - | X | = 2 n , | Y | = 2 m , | Q | = 2 k .

For automaton A, its functions δA and λA can be defined not only on the set X of all characters of the input alphabet (letters), but also on the set X * of all input sets of letters - words . For any input word (χ = x 1 x 2  x 3 ... x k )  X * and any letter x j

δ ( q i , χ x j ) = δ (δ ( q i , χ), x j ).

Using the extended function ной, the extended output function λ is inductively determined:

λ ( q i , χ x j ) = λ (δ ( q i , χ), x j ).

We assign to each input word χ = x 1 x 2  x 3 ... x k the word γ in the output alphabet:

γ = λ ( q 1 , x 1 ) λ ( q 1 , x 1 x 2 ) λ ( q 1 , x 1 x 2  x 3 ) ... λ ( q i , x 1 ... x k ).

This correspondence, which maps input words into output words, is called an automaton mapping , as well as an automaton operator implemented by an automaton (A, q 1 ) . If the result of applying the operator to the word χ is the output word γ, then this is denoted by A (χ) = γ. The number of letters in the word χ is called the length and is denoted by | χ |.