Quantum cellular automata

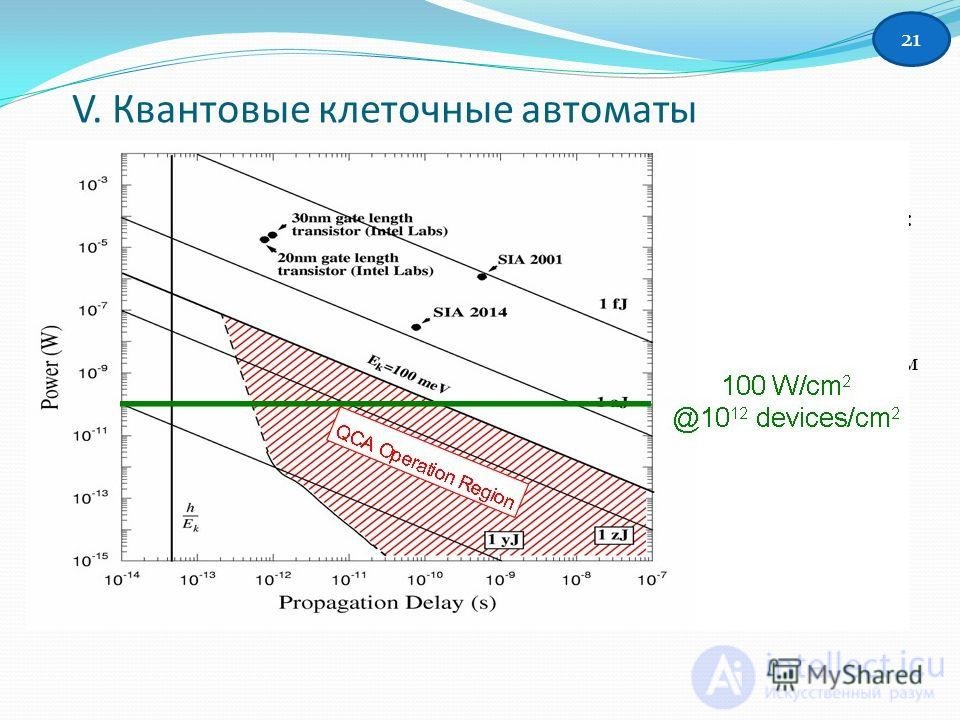
The Landauer principle states that regardless of the physics and technology of the computational process, if one bit of information is lost in the calculation process, energy is released that is at least equal to kb Tln2 (here and below: kb is the Boltzmann constant, T is the absolute temperature). Each transistor loses 1 bit of information whenever it is triggered, and the energy released by it in practice turns out to be approximately 500 times more than the fundamental minimum set by Landauer. Calculations based on the Shannon von Neumann-Landauer principle (developing the Landauer principle) and using the Geisenberg uncertainty principle show that if, according to the ITRS plan, by 22-nm technology will be used by 2016, the processor will generate heat even when using ideal materials 5–10 million watts / cm 2 RW Keyes and R. Landauer. Minimal energy dissipation in logic // IBM J. R & D, vol. 14, Mar - pp. 152–

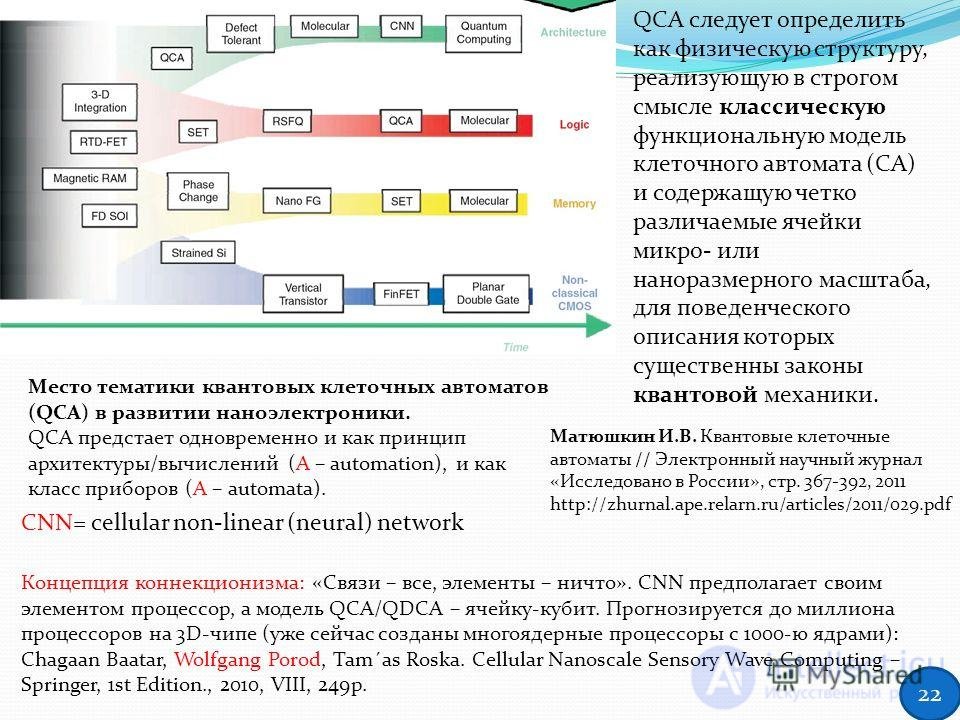
22 Place of the subject of quantum cellular automata (QCA) in the development of nanoelectronics. QCA appears at the same time as the principle of architecture / computing (A-automation), and as a class of devices (A-automata). QCA should be defined as a physical structure that in the strict sense implements a classical functional model of a cellular automaton (CA) and contains clearly distinguishable cells of a micro or nanoscale scale, for the behavioral description of which the laws of quantum mechanics are essential. CNN = cellular non-linear (neural) network Connectionism concept: "Connections are everything, elements are nothing." CNN assumes its element processor, and the model QCA / QDCA - cell-qubit. Up to a million processors on a 3D chip are predicted (multi-core processors with 1000 cores are already created): Chagaan Baatar, Wolfgang Porod, Tam´as Roska. Cellular Nanoscale Sensory Wave Computing - Springer, 1st Edition., 2010, VIII, 249p. Matyushkin I.V. Quantum cellular automata // Electronic scientific journal "Research in Russia", p. 22

23 Anton Zeilinger, 1988 R. Feynman. Simulating physics with computers // Int. J. Theor. Phys. 21 (1982) G. Grossing and A. Zeilinger. Quantum cellular automata // Complex Systems 2 (2), 1988: pp. 197–208 and 611–623. Craig S. Lent et al. Quantum cellular automata // Nanotechnology 4 (1993) Wolfgang Porod. Quantum-dot devices and quantum-dot cellular automata // J. Franklin Inst. Vol. 334B, # 5/6, pp, 1997 Richard Phillips Feynman, 1965/1982 Craig S. Lent, 1993 Wolfgang Porod, 1997 There is also a third point of view on QCA as a mathematical model of a quantum-size device and / or system, for example, a lattice "Gas" (quantum lattice gas). Such a model (Vatrouza-van Dam) should, if necessary, contain psi functions to describe the state of the cell and work with state transition matrices. The second condition - the zero (ground) ground state in the cell and in its entire neighborhood necessarily generates a zero. The Ising spin model shows a boundary case between the classic CA and the QCA. QDCA = quantum dot cellular automate Historically, there was a synthesis of a rather old idea of ​​parallelism of computations and cellular automata in the 1940s. XXth century and research results in theoretical physics (from the 90s of the 20th century to the present) of quantum dot ensembles, including non-atomic ones (based on nanocrystals). The three-valuedness and inconsistency of the QCA definition is related to this. A major contribution to the development of QCA was made by the research group of the University of Notre Dame (Indiana, USA), funded by the DARPA programs, as well as the QUADRANT project implemented in the years. in accordance with the European Commission's MEL-ARI (Microelectronics Development Research Initiative) program and joined the efforts of the universities of Pisa, Cambridge, Tübingen and other cities of Europe and North America, including Notre Dame. The last 5 years there has been a stagnation of QCA-related themes, perhaps temporary. 23

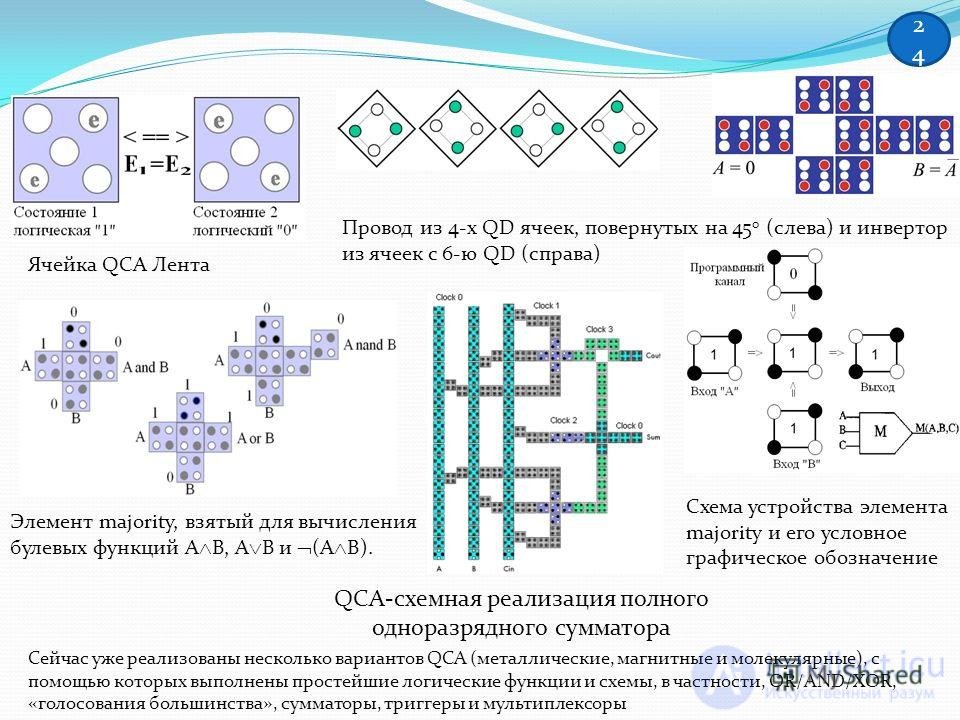
24 QCA cell Ribbon Wire of 4 QD cells rotated by 45 0 (left) and inverter of cells with 6th QD (right) The element of majority, taken to calculate the Boolean functions AB, AB and (AB). The device of the majority element and its conventional graphic designation QCA-circuit implementation of a full one-bit adder Several versions of QCA (metallic, magnetic and molecular) have already been implemented, with the help of which the simplest logical functions and circuits, in particular, OR / AND / XOR, are performed, majority voting, adders, triggers and multiplexers 2424

25 In 1994, Lenta developed (without a physical implementation!) A single-digit adder with three inputs, containing on an area of ​​1.5 μm 2 more than 100 QCA cells with a QD size of 10 nm, which had ultra-low power consumption and fast response in the terahertz range; for the implementation of such a logical element in the classical version would need about 30 transistors. In a more abstract form, the advantages of QCA over CMOS basis were summarized by Tape in his first work: eliminating the need for multilayer metallization due to the locality of the interaction between cells, which also does not require energy costs for transferring / switching the signal inside the cell, as well as removing the need for substantial energy transfer to the inside of the QCA array (concept of terminal computing); ultra-high packing density of logical elements (if we take the design standard for 10 nm, and the linear size of the cell for 50 nm, then the density will be about bits / cm 2); ultra-low energy dissipation at the W / bit or B level to the switching of the bit state, which is caused by the cell being in one of two ground (energy) states and proximity of the excited state (QCA is assumed to function at a temperature near 0K); ultrafast calculations due to the fact that relaxation inside the cell is achieved by phonon-phonon and electron-phonon interactions; in particular, the switching time of the majority element is estimated in ps. In 2007, a QAs based on GaAs / AlGaAs was experimentally implemented. The possibility of implementing semiconductor QCA, technologically compatible with the basic processes of micro-and nanoelectronics, still remain underestimated. 25

26 Micrograph and cell diagram of a metallic QCA. The red circles show 4 islands of aluminum, the violet ones show the islands of aluminum necessary for electrometric measurements. Tunnel junctions between QDs are shown by two adjacent strips. The main advantage is the relative simplicity of the technological route of their manufacture, which involves only three basic operations, as well as good cell homogeneity (transition resistance varies between 20-30%) and a high percentage of yield. The main disadvantage is associated with the need to maintain cryogenic temperatures due to the low (compared to kb T) energy needed to activate Al QD - eV. A magnetic QCA cell diagram (left) and a photograph of 64 nanomagnetic QCA wires obtained using atomic force and magnetic force microscopy (right) The advantage of this QCA class is to operate at room temperature, but the main drawback is large inertia (in In particular, the maximum switching frequency of the signal is estimated in k Hz). However, in the 2009 edition of the Trip Map, magnetic QCAs are considered a promising direction of “nanomagnet-based logic”. The study of molecular QCA is considered to be the most promising. Their main idea is the ability of molecules to store a charge, and for charge transfer, much more is required. Olive activation energy than kb T, and there is no need for currents to flow between molecules. Since the size of the molecule usually lies in the range of 1-2 nm (which potentially gives the ultra-high density of qubits cm -2), the capacitance C of such a molecular structure is small, and the activation energy is estimated as e 2 / C. One large molecule can completely represent the QCA cell Tape. 26

27 Three general requirements for molecules used in QCA can be formulated: A molecule must have at least two stable charge configurations, i.e. be bistable; as a rule, the presence of metals (or groups) with variable valence or the possibility of oxidation / reduction of sterically removed atomic complexes provides such a requirement; The molecule must be in chemical contact, i.e. form a strong chemical bond with the substrate (usually with silicon); The charge configuration of the molecule can be changed under the influence of the neighboring molecule through the Coulomb interaction. The structure and electron density, calculated ab initio, for the decatriene cation molecule. The first requirement means the presence of two minima and one maximum between them on the Gibbs energy profile. When implementing the second requirement, it is necessary to take into account that changes in the configuration of groups of variable valence do not affect the strength of the bond of the entire molecule with silicon. It should be noted that the presence of the contact of the molecule with the substrate considerably complicates the ab initio calculations of such molecules. In fig. one of the candidates is shown, namely, 1,5,9 - decatrion cation, three double C = C - bonds correspond to three QD and cause three steady states "0", "1" (active) and "null" (main); the activation energy is 0.15 eV (respectively, the value of the timing field is several V / nm), and the switching time is approximately c. 27

28 Among the candidates for the role of the active molecule were considered: 1,4 - diallylbutane cation (the molecule is short, just over 0.7 nm in size, and the tape cell is realized by four allyl groups on two molecules with an activation energy E kink = 0.55–0.65 eV); Organic cobalt compound with four ferrocene groups {(η 5 -C 5 H 5) Fe (η 5 -C 5 H 4)} 4 (η 4 - C 4) Co (η 5 -C 5 H 5) 2+ (cell The tape is realized by one molecule); Silicon phthalocyanine (a group of phthalocyanines is widely used in pharmacology, and there are attempts to use them in solar energy); Endohedral fullerenes (the spin of an atom trapped inside a fullerene, for example, 60, provides the possibility of magnetic-dipole interaction of qubits, and the implementation of logical functions differs from the Ribbon scheme and is based on the alternation of two or three types of endohedral fullerenes) - it is possible that such QCAs related taking into account the spin of the atomic nucleus, in a separate class. General view of molecular QCA. Under the surface of silicon with dekatrien molecules attached to it, control electrodes are located that carry signals of lines A, B, C, D (the Boolean function F (A, B, C, D) is calculated) and timing electrodes. The question arises how to read the states of molecular QCA cells nondestructively? 28

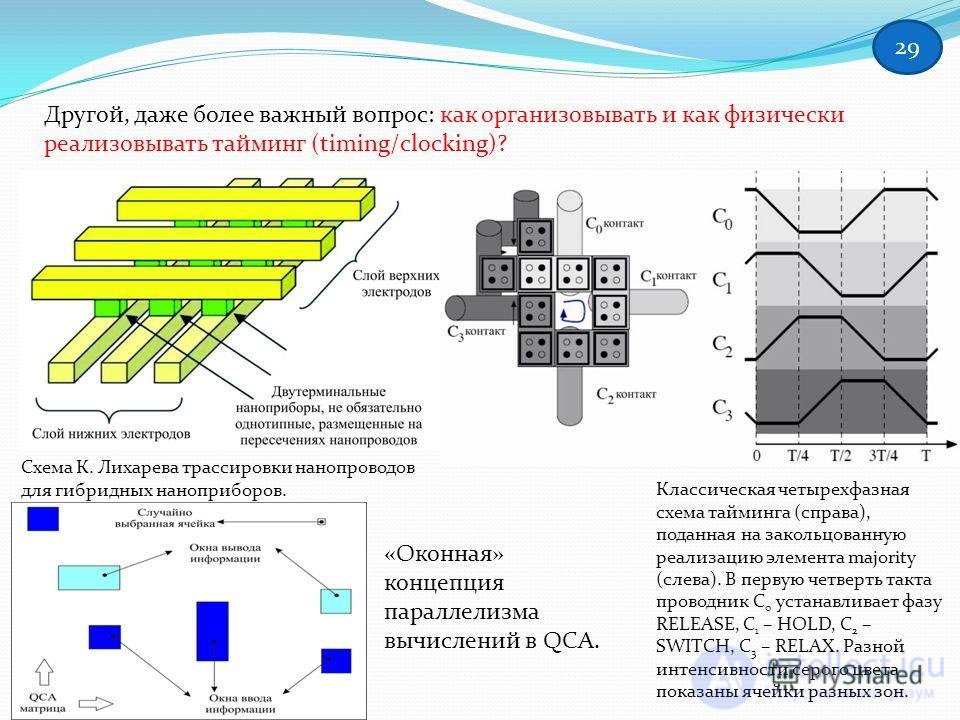
29 Another, even more important question: how to organize and how to physically implement timing (timing / clocking)? Scheme K. Likhareva trace nanowires for hybrid nanodevices. The classic four-phase timing scheme (right), filed on the looped implementation of the majority element (left). In the first quarter of the cycle, C 0 sets the RELEASE phase, C 1 - HOLD, C 2 - SWITCH, C 3 - RELAX. Different intensity of gray shows the cells of different zones. The "window" concept of computation parallelism in QCA. 29

30 Ribbons showed that classical calculations can be implemented using QCA based on cells of 4-6 quantum dots (which generated a wave of publications related to the corresponding CAD systems and the issues of reversibility of calculations, heat generation, calculation of delays and traces in QCA). But this was achieved by imparting the QCA features of the pseudo-one-dimensionality of the “World-Wire” model, due to the entrainment of quantum mechanisms of inter-and intracellular interactions. Such constructions as QCA-wire, in our opinion, are a palliative and a compromise, suggesting the direction of the information flow, and therefore, they realize sequential calculations. Thereby, the prospect of parallelism of calculations, which was originally incorporated in QCA, is artificially reduced and shaded. In other words, in the term “quantum cellular automata” one should put more emphasis on the word “cellular” rather than “quantum”. The idea of ​​terminal computation remains underestimated, in particular, by its authors. Summarizing, it can be proposed to divide the QCA cell into three groups according to the functional role: approximately 5-10% of the cells retain their state unchanged, being a “window” for entering information into the QCA; about 5-10% of QCA cells provide their quantum (eg, charge) state for reading / detection, being a “window” of information output; the remaining 80-90% of the cells are controlled only by the timing scheme, and their array is used for low-level information processing. Such an understanding of the idea of ​​terminal computing presupposes the absence of an information transfer vector (in particular, one should abandon the naive-spatial idea of ​​the location of input and output cells at opposite ends of the QCA), as well as the deliberate rejection of monitoring the state of all QCA cells. The latter peculiarity, due to the desire to reduce energy dissipation, and for molecular QCAs, which is absolutely necessary due to the influence of the measurement process on the qubit wave function, gives additional features of “quantumness” QCA, i.e. in essence, we will not know in principle what happens inside the QCA during the calculation. However, it should be clearly understood that such a radical change in the computing paradigm implies intensive work by mathematicians (despite the successes they have achieved, for example, in establishing the fact of Turing-completeness of the Conway game). In other words, complex physical processes occurring in the aggregate QCA cells undoubtedly mean a transformation of the global information state of the QCA, but can we direct this transformation in the right direction? A negative answer is not excluded, and then we will have to return to the “World Wire”. One of the objections to the QCA-wire was the possibility of an uncontrollable reverse, i.e. opposite in the direction of propagation of the signal, the influence of the cells on each other. thirty