Simulation of systems with distributed parameters when moving material masses

Once again we will complicate the task from the previous lecture.

Consider the processes of heating, drying and simultaneously moving non-uniform mass. Now (see fig. 18.1) we will not only dry the mass, but also, in the process of drying, move it along the conveyor to the consumer. Let the length of the conveyor - L , and the linear speed of its movement - V. For realism, we will improve the model, taking into account two parameters of the “heap” - the temperature T and the humidity W of each of its sections. The initial state of the raw material located in the bunker 1, we denote as T ₀ and W ₀ .

Fig. 18.1. Diagram of the process of drying and moving raw materials

To distinguish different mass fragments not only by layers, but also on different parts of the conveyor, we introduce the division of mass into zones. Let there be a total of n layers and k zones.

The time h during which the tape moves in one zone is:

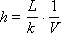
The idea of ​​modeling is that we will carry out heating and drying (calculation of temperature and humidity) in zones and layers with a temporarily stationary conveyor, and then move the raw material from zone to zone simultaneously, simulating the movement of the conveyor.

That is, for computer simulations on digital machines, it is useful to separate the drying process and the moving process. So on one tick of time Δ t it makes sense to carry out several MICROTACT drying a . It is just as many microtakes of the tape as if standing still. After this, there is a sharp shift of the conveyor, and the raw materials from one zone fall into the next zone with a jerk. After this, the drying process in the new position of the conveyor is carried out again.

The relationship of the quantities Δ t , h and a is given by the formula: Δ t = h · a or so:

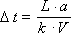
Next: T _cf. - ambient temperature; T _Н - heater temperature ( T _{Н j} = g · U _j ); T _tr. - the temperature of the conveyor belt.

...

...

...

...

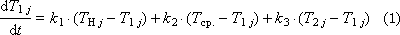
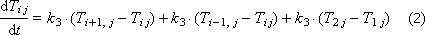
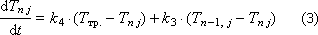
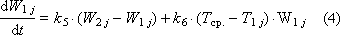
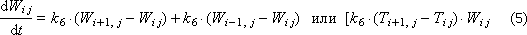
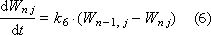
Then the behavior of the “heap of raw materials” system is described by a system of differential equations, each of which describes a separate layer and a “heap” zone both in temperature and humidity.

The algorithm for calculating such a system is shown in Fig. 18.2. A feature of the algorithm is that it contains, in addition to the cycle in time and layer (see the algorithm in Figure 17.2), another nested loop by zone number. Indeed, on each measure, it is necessary to separately calculate the changes not only in each of the heap layers, but in each zone.

Fig. 18.2. Flowchart simulation of distributed dynamic process with moving masses

So, a tool for modeling systems distributed over several coordinates is repeatedly nested cycles - inside the cycle “over time” there is a cycle “along one axis of space”, inside this cycle there is another cycle “along another axis of space” and so on. The processes, if possible, are separated - the drying cycle is separated from the mass movement cycle, the cycles of the processes stand one after another .