Each time step of the automaton consists of two stages: analysis of the situation, in
every cell; movement of particles in accordance with the rules of the machine.
three directions ("forward", "right", "left"). This takes into account the state N
models.
where i, j are the coordinates of the current cell, X is the state of the neighboring cells. If at
sequential inspection of the cells meets the wall, then all subsequent cells
are considered full, as they are inaccessible.
The probabilities found are used in the second stage. Consistently
three directions of movement are checked (“forward” or “to the side”), if at least
one of them is free - the particle moves. If the three nearest cells are occupied -
the particle moves backwards.
Thus, the particles move through the cells of the automaton in accordance with
following rules:
• if possible, the particle moves forward (with respect to some
given direction);
• if forward movement is impossible, the particle moves to the right / left or back;
• the presence of other particles or walls in any direction reduces
probability of particle motion in this direction.
tasks
21
• Place a few fish on the field. Allow them to multiply. Further
put a few sharks. Change the parameters of the shark population so that
the fish are extinct. Give the values of these parameters.
• The same, but to achieve the extinction of sharks, changing the parameters of the fish, lead
values of these parameters.
9.3. Line Automatic
• Determine the dimension of the resulting pattern.
• Investigate the effect of parameters on the dimension and configuration of the pattern,
Build and save relevant graphs for the report.
9.4. Cellular automaton, simulating the movement of the crowd
• Create a closed area (17x12 cells), with the only way out of 3
cells. Build dependencies of the number of people out on time for different
initial fill density values. Take time to complete
people and analyze its dependence on time.
• Repeat the construction for a different output width N, where N varies from
2 to 10. Build the dependencies of the time of complete exit of people from the width.
exit.
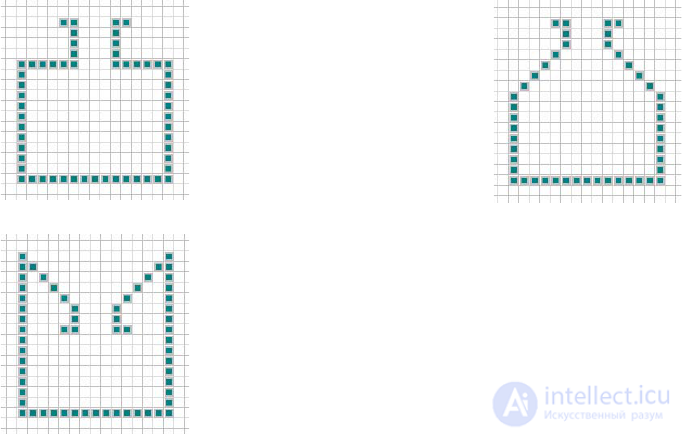
• Create an area that looks like a bottle with “sharp” edges (fig. 17a).
Build dependencies of the time of exit of all people from the area on the density
initial fill and on exit width.
• Create a bottle-like area (fig. 17b). Build a dependency
the time of exit of all people from the region from the density of the initial filling and from
output widths. Compare the results with those obtained in the previous task.
• Create an area similar to the non-spill inkwell (Fig. 17c).
Build the dependence of the time of exit of all people from the area of density
initial fill and on exit width. Compare results with
received in previous assignments.
Figure 17. Areas of study
Test questions.
1) What is the "speed of light" in the game "Life" Conway?
2) What is the speed of the airframe?
3) How many cells does the minimum stable configuration consist of?
4) Why does the population in “Aqua-Tore” with an infinite amount of food grow not
infinitely?
5) How is the fractal dimension calculated?
6) What is the dimension of the Sierpinski carpet?
7) Which cell automata are reversible and
why?
8) Find an analytical solution of the Ferhulst equation
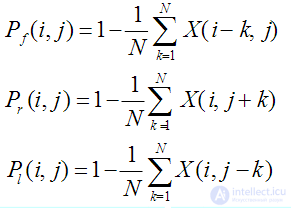 (five)
(five) 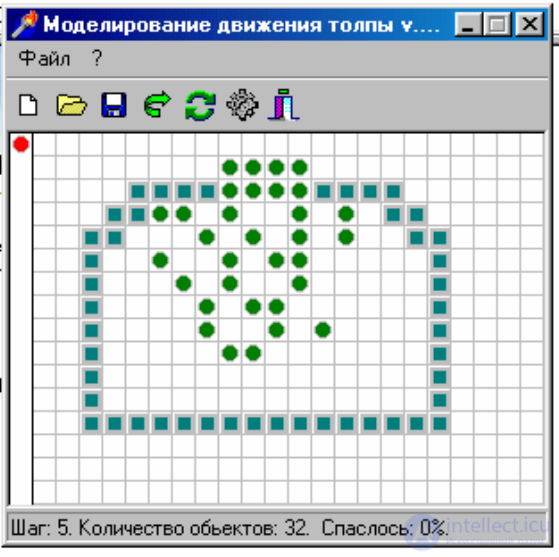


Comments
To leave a comment
System modeling
Terms: System modeling