Delay systems

Delay systems theories study systems where the response to an input signal does not occur instantaneously, but with some delay (lag). Lag is the time interval that occurs between the action on the system and its reaction to this action. Such systems are important in applied sciences and engineering, since lag is often present in real-world processes - from data transmission in networks to chemical reactions, biological processes and economic models.

Types of lags:

• Constant lag: the delay is fixed and does not change over time.
• Variable lag: the delay varies depending on the operating conditions of the system.
• Discrete lag: the delay has a fixed value and manifests itself as a single event.
• Distributed lag: the lag is distributed over time, which makes it difficult to analyze.

Examples of systems with delays:

• Technical systems: control systems where controlling an object results in changes with a delay. Examples: thermal systems (heating), electronic networks and signal transmission.
• Biological systems: physiological processes such as hormonal reactions, respiration, blood flow.
• Economic systems: market models where the impact of economic factors (for example, a change in the interest rate) does not lead to immediate results, but has an effect after some time.

Linear system with delay

A linear delay system is one that contains at least one link in its structure, in which there is an invariable time delay τ of the change in the output coordinate after the change in the input coordinate begins.

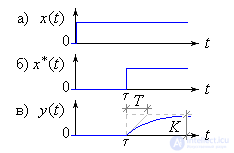
Consider a first-order aperiodic link, which is described by the equation:

T · dy / dt + y = K · x (t).(1)

The equation of the corresponding link with delay τ will be:

T · dy / dt + y = K · x (t − τ).(2)

It is called differential-differential.

Denote x * (t) = x (t − τ), then equation (2) is written in the ordinary form:

T · dy / dt + y = K · x * (t). (3)

Consequently, its transient response corresponds to the aperiodic link (Fig. 1c), but is delayed by τ s, which is determined by the exposure delay x * (t) (Fig. 1b).

Summary:

• The time characteristic of any link with delay will be the same as that of the corresponding ordinary link, but only shifted along the time axis to the right by the value of τ.
• The magnitude of the delay τ in the link can be determined experimentally, by removing the time characteristic.

Example of a system with a transport delay

PF link clean lag

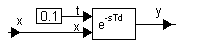
The properties of the link are such that y (t) = x (t − τ), where τ is the delay, and x (t − τ) = 0 for 0

We expand the right side of the equation (i.e., the output signal) into a Taylor series:

,

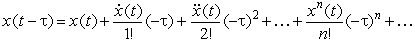or

,

those.:

.

Net lag link approximation

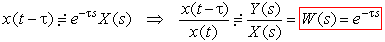Work Files: [Approximators]

Compare the transition functions of the aperiodic link with the retarded argument and the aperiodic link of the 2nd order:

Since they are substantially similar, in approximate calculations it is possible to make substitutions for the transfer functions of the links.

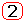In some cases, taking into account a large number of N links in a system with small time constants ΔTi and a unit transfer coefficient is applied, one link with a constant delay equal to the sum of these time constants τ = ∑ΔTi≈N · ΔT. Those.:

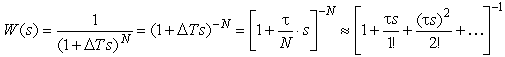
If N → ∞, then in the limit we obtain W (s) ≈e − τs. Already at N = 8 ÷ 10, the degree of approximation is high. The series will more closely correspond to the expansion in the series of the function e − τs, if it is represented not by aperiodic, but by phase-shifting links.

Opening systems with delay

Most methods for studying the stability or quality of systems use the PF system for the open state W (s) as input. The pure lag link is a non-linear element, and it complicates both analytical analysis of systems and machine (mathematical modeling programs cannot perform analysis functions for systems with non-linear elements). Therefore, they either use linearized approximants of the pure lag link, or open the system in the branch that contains the pure lag link so that the FS has the form: W (s) = Wo (s) × e − τs, where Wo (s) is the FS of the system no lag.

Consider and disconnect the system with the main options for the inclusion of the pure lag link - serial, parallel and in the OS chain:

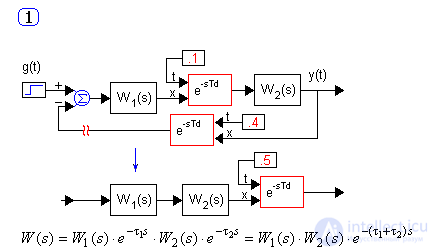
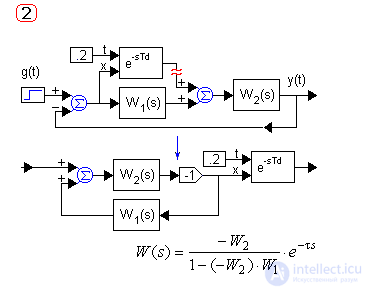
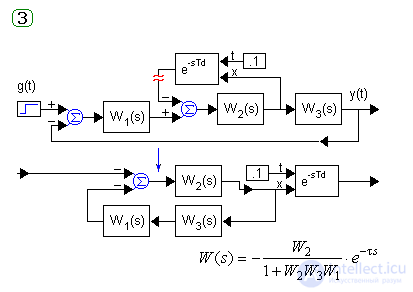
If the links of pure lag are in different branches of the structural scheme, then their approximants and machine methods of analysis are used for research.

Frequency properties of systems with delay. Critical Delay Concept

Let's move to the frequency domain:

W (jω) = Wo (jω) × e − jωτ = Ao (ω) · ejφo (ω) × 1e − jωτ,

Consequently:

L (ω) = | W (jω) | = Ao (ω) × 1 = Ao (ω),
φ (ω) = φо (ω) −ωτ.

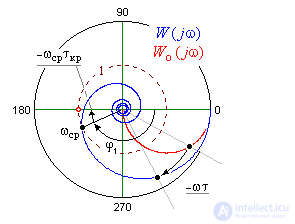
Summary:

• Thus, the presence of a link with delay does not change the modulus, but only introduces an additional phase shift (–ωτ).
• It can be seen from the graph that the e − τs link twists the initial hodograph Wо (jω) clockwise, worsening the conditions of stability.
• According to the available hodograph Wo (jω), you can determine the critical value of the delay τcr:
  φ1 − ωсрτкр = −π => τкр = (π + φ1) / ωср
  In some cases, τcr can be calculated analytically.

Sustainability systems with lag

Consider a closed system:

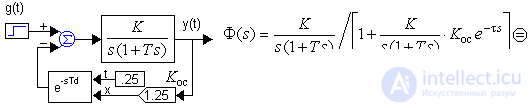
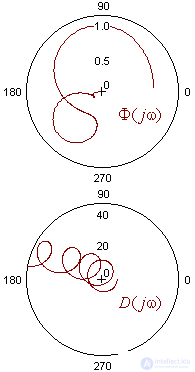
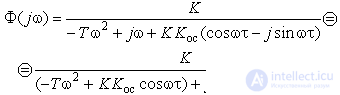
By the denominator of the CF Φ (jω), in the general case the characteristic equation will have the factor e − τs, which determines the possibility of the presence of an infinite number of roots (see the Mikhailov hingograph D (jω)).

As before, for stability, they must all have negative real parts.

• For the stability of the systems of the 1st and 2nd order with a delay, the positiveness of the coefficients is not enough.
• For systems of the 3rd and more orders, the criteria of Vyshnegradsky, Raus, Hurwitz are not applicable.

On the study of the accuracy of systems with delay

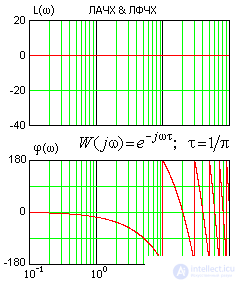
The pure delay of the link for the pure lag link shows that its transmission coefficient is equal to one in the entire frequency range. Moreover, in the low-frequency region, the delay in the link is negligible (i.e., the phase shift tends to zero), therefore, in studying the accuracy of systems with delay, it is permissible to simply exclude all the links of the pure delay from the block diagram. This operation is permissible, since the accuracy of any system is determined only by the low part of its response.