Another cellular automaton that hides behind seeming simplicity
very interesting object. The idea is quite simple - the ring serves as the field for the machine.
one cage thick. The next generation is obtained from the previous and
displayed under the whole structure. Thus, we have a plane, one by one
the axis of which is the only spatial coordinate, and on the other is time, in
As a result, we can view the entire evolution of the population.
The rules of the machine are pretty simple - they are similar to the rules of "Life" in
one dimensional case.
• if the number of neighbors over the test cell is 3, the cell is “born”
• if the neighbors are less than 2 above the cell, then it “dies”.
In the process of the development of such a population, a very interesting pattern is obtained -
"Sierpinski napkin".
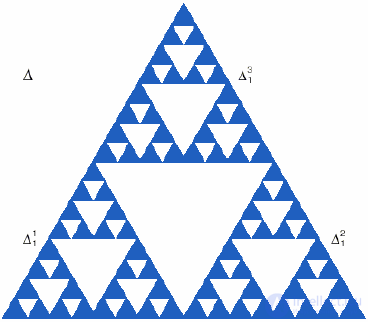
Napkin Sierpinski - fractal, which is constructed as follows.
The right triangle is divided by the middle lines into four equal triangles and
the inside of the center is thrown away. With the three remaining ones do the same and
so ad infinitum. After a countable number of discards, the set S remains,
called a Sierpinski napkin. In fig. 10 shows a napkin on the third
step.
uh
Fig. 10. Sierpinski Napkin
practical task
• Determine the dimension of the resulting pattern.
• Investigate the effect of parameters on the dimension and configuration of the pattern,
Build and save relevant graphs for the report.
 uh
uh
Comments
To leave a comment
System modeling
Terms: System modeling