2.3. Symmetric block encryption 2.3.1. Basic principles of symmetric block encryption

As already noted, block ciphers process the message to be encoded in blocks of several bytes, and the plaintext block X is converted into a ciphertext block Y of the same size using some Key encryption key:

Y = Encrypt (X, Key)

The decryption procedure performs the inverse transform using the same key:

X = Decrypt (Y, Key)

In the general case, the procedures Encrypt and Decrypt do not coincide, however, if the sequence of actions for encryption and decryption is exactly the same, the block cipher is said to be absolutely symmetric. For an absolutely symmetric cipher, obviously, fair:

X = Encrypt ((Encrypt (X, Key), Key)

The Encrypt and Decrypt conversions interpret blocks of open and ciphertext as whole numbers and perform a series of arithmetic or logical actions on them, the main task of which is to carefully “mix” the bits of the plaintext block between them and also link them with the bits of the encryption key used to form the block closed text. In order for the entire ciphering transformation to be reversible, the actions, its components must also be reversible (the reversibility of the action means that according to its result and one of the operands you can get the second operand). Table 2.1 provides a list of reversible operations used in modern cryptographic transformations [6].

Among the operations listed in the table, it is necessary to distinguish multiplication and table substitution, which belong to the non-linear class and significantly complicate the methods of linear cryptanalysis of block ciphers.

Table 2.1

Major reversible operations

Operation name	Graphic designation	Formula conversion	Inverse transform
Addition		X ' = X + V	Subtraction
Addition modulo 2		X ' = X Å V	Auto reverse
Multiplication modulo 2 N +1 (N is the block size)		X ' = (X × V) mod (2 N +1)	The multiplier can be found by the Euclidean algorithm
Right / left cyclic shifts		X ' = X ROR V X ' = X ROL V	Backward shift
Table substitution		X ' = SBox (X)	Backward substitution

For parameter transformations of cryptoalgorithms that do not require reversibility, irreversible operations are used, such as logical addition and multiplication, arithmetic left and right shifts, obtaining the remainder of integer division, modulo-2 multiplication.

As the second operand V, involved in the operations of cryptographic transformations, can be used:

1) fixed numeric constants;

2) the values ​​calculated from the independent part of the block to be encrypted (for example, the youngest and highest parts of the block of encrypted information can be added);

3) key material - a block of information calculated solely on the basis of information stored in the encryption key.

One of the basic principles of the structural construction of modern cryptoalgorithms is the principle of iteration. His idea consists in multiple processing of a single plaintext block consisting of several cycles (or rounds) using a special key for each round, calculated on the basis of an encryption key. The number of cycles can be varied for reasons of cryptographic strength and efficiency of the implementation of the algorithm: an increase in the number of cycles leads to an increase in the strength of the cipher, but increases the encryption time and consumed computing resources. Such cyclical structures are commonly called networks, and most modern block ciphers are built using network architecture.

As an example of cryptographic networks, there are SP networks that contain two layers in each round - substitution, in which reversible transformation operations are performed on the encrypted block and key material, and permutations (permutation), in which the bits are rearranged inside the block . However, the most popular today is the Feystel network, the scheme of which is shown in Fig. 2.4.

When encrypting a block of plaintext is divided into two equal parts - left and right. On each cycle, one of the parts is transformed using the generator of the function F and the auxiliary key k _i obtained from the original key. The result of the conversion is folded modulo 2 with another part, after which the parts are interchanged. The transformations on each cycle are identical, and only after the last round the block parts are not rearranged.

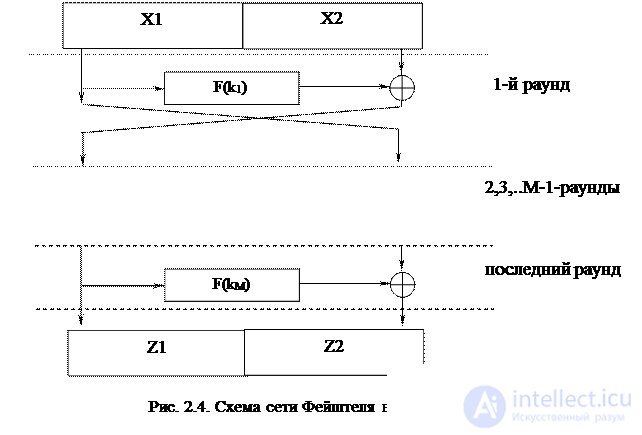
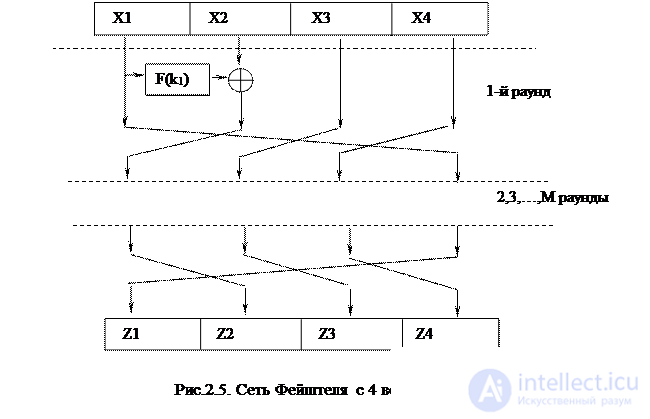
If the size of the cryptographic encryption block is too large, modifications of the Feystel network with 4 branches are possible, one of the variants of which is shown in Fig. 2.5. The advantage of the Feystel network is that the decryption is performed by the same sequence of transformations, only the order of the auxiliary keys is reversed. This is achieved by the auto-reversibility of the modulo-2 sum operation, which mixes the parts of the block together.