4. Electronic digital signature.

Another important security service of information systems is recently becoming the authentication of information, which is understood as establishing the authenticity and immutability of a message, establishing and proving the authorship of a message, and proving that a message has been received. This service is especially important in the field of financial and legal electronic document management. To solve the problem of information authentication today, the concept of electronic digital signature (EDS) is used. A digital signature is a set of methods that allow you to transfer the properties of a handwritten signature on a document to the field of electronic document circulation. A real signature has the following properties:

1. the credibility that the user knowingly signed the document;
2. the authenticity of proving that a particular user, and no one else for him signed the document;
3. the inability to reuse the signature on one document to sign another;
4. immutability of the signed document;
5. the materiality of the signature, which does not allow the signatory to subsequently refuse it and the document.

The same properties should have an electronic digital signature, for which it is based on cryptographic methods. Consider the implementation of electronic digital signature based on the RSA algorithm (Fig. 4.1).

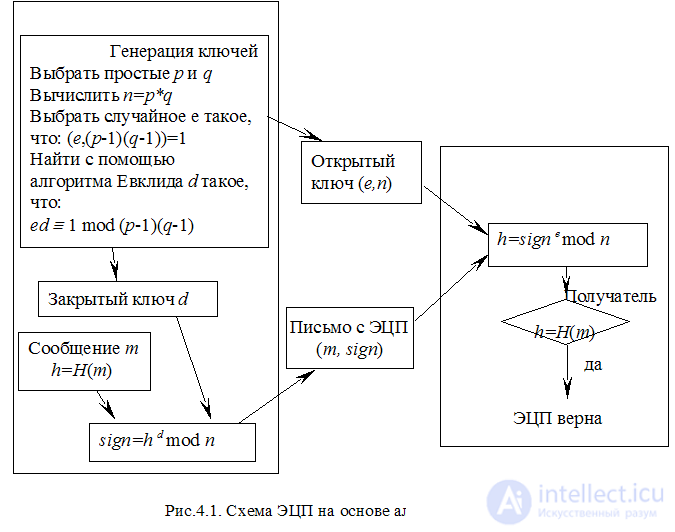
Unlike the encryption algorithm, the sender here is the owner of a private / public key pair. The procedure for generating an electronic signature sign under a message is similar to document encryption, but the deduction of the private key d by deducting n does not result in the message itself or its parts, but the message digest h . An integral part of EDS algorithms is information hashing, in the figure it is denoted by H (), and this can be any of the hashing algorithms discussed in Chapter 2.5.

The message m with the signature sign will be uniquely authenticated. The authorship of the message can be established and proved for a pair of keys ( d , e ) using certification under the scheme described in 3.2. The attacker will not be able to replace the message m (or rather, it will be very difficult for him to do this), because he needs to replace another message m ' instead of message m, satisfying it and having the same hash function as m , which is computationally difficult task. For the same reason, the attacker will not be able to use the intercepted signature of the sign to sign another document, because another document will receive a different value of the hash function h , and it forms the basis of the signature. Thus, all the necessary signature properties by the described algorithm are provided, as for the cryptographic strength of the EDS method, it is determined by the cryptographic strength of the asymmetric cryptographic method used and the unidirectional encryption function. It should also be noted that the message m itself is transmitted in open form. In order to ensure the confidentiality of the information transmitted therein, the use of additional encryption is required in a symmetric or asymmetric scheme (in this case, encryption on d key will not ensure confidentiality, since the message can be decrypted by public key e ).

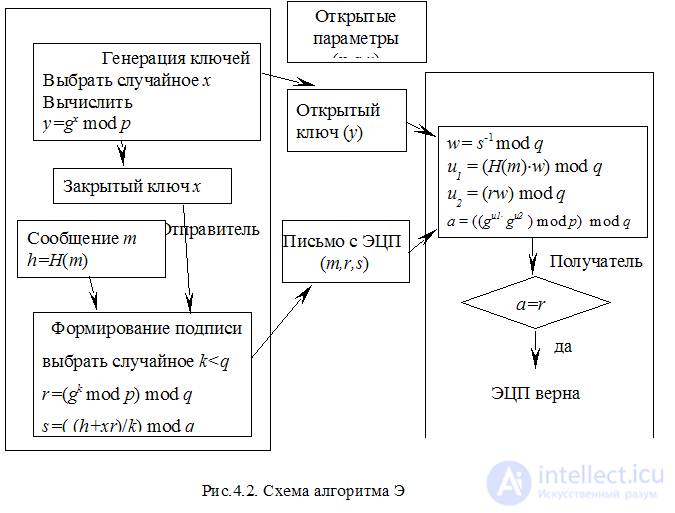
EDS schemes based on the ElGemal algorithm are very popular, which is due to both the proper robustness of the algorithm and the better computation speed compared to RSA. In particular, the DSA (Digital Signature Algorithm) DSA (Digital Signature Algorithm), which is a variation of ElGemal's EDS algorithm in the Schnorr modification, is used in the standard of the United States National Standards Institute. The algorithm uses the following open parameters:

• p is a prime number in the range from 512 to 1024 bits;
• q -160-bit prime number, divisor p -1;
• v is any number, v < p -1, such that v ( p -1) / q mod p > 1;
• g = v ( p -1) / q mod p ;
• y = g x mod p .

The secret key is any 160-bit number x , x .

The DSA EDS algorithm in graphical form is presented in Figure 4.2.

There are many modifications of the ElGemal scheme. One type of modification was the transfer of calculations to a group formed by elliptic curves [14]. About elliptic curves as a mathematical apparatus for the implementation of asymmetric cryptoalgorithms have already been discussed in Chapter 2.4.2. Consider the properties of elliptic curves in more detail.

For practical use in cryptography, elliptic curves (EC) are used, defined over Galois fields. Let a prime number p > 3 be given. Then an elliptic curve E defined over a simple finite field F p is the set of pairs of numbers ( x , y ), x , y ∈ F p , which satisfy the identity:

y 2 = x 3 + ax + b mod p ,

where a , b ∈ F p and ( 4a 3 + 27b 2 ) ≠ 0 mod p . In addition, an infinite point I is added to the elliptic curve. Thus, the points that satisfy the equation of the curve E , and the point I form a finite Abelian group.

The geometrical representation of an elliptic curve is shown in fig. 4.3.

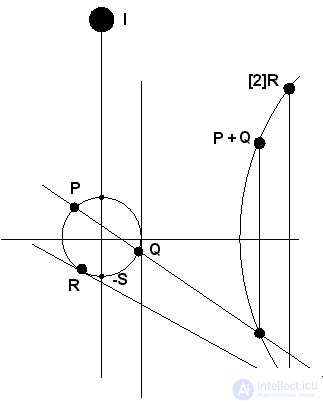
Fig. 4.3. Elliptic Curve Graph

For points of an elliptic curve, the operation of addition is defined. For two points belonging to the curve E , P ( x p , y p ) and Q ( x p , y p ), the point that is their sum will also lie on the elliptic curve. The coordinates of the point S = P + Q are defined by the following expressions:

• k = ((y q -y p ) / (x q -x p )) mod p
• x s = (k 2 -x q -x p ) mod p
• y s = (k (x q -x p ) -y p ) mod p

Point S can be obtained graphically by simple constructions. To do this, a straight line is drawn on the graph through the points P and Q , and the point of intersection of this straight line with EC is mirrored relative to the axis OX (see Figure 4.3).

If the points P and Q coincide, then we get the point S = 2 * Q. Then its coordinates are determined differently:

• k = ((3 * x q 2 + a) / (2 * y q )) mod p
• x s = (k 2 -2x q ) mod p
• y s = (k (x q -x s ) -y p ) mod p

Graphically, doubling a point can be obtained by plotting a tangent to a point and reflecting the intersection point of a tangent with an elliptic curve relative to the OX axis (see points R and 2 R in Fig. 4.3). From this it is obvious that one can define the operation of multiplying a certain point of an elliptic curve by an integer, which allows determining the point Q = k * P (the point P multiplied by the integer k turns into a point Q ). Scalar multiplication is performed by several combinations of addition and doubling of points of an elliptic curve. For example, the point 25 * P can be represented as 25 * P = 2 * (2 * (2 * (2 * P )) + 2 * (2 * (2 * P ))) + P. With the operation of multiplying an EC point by an integer, the idea, reliability and cryptoresistance of elliptic cryptography are directly related. The point is that the ECDLP problem (Elliptic Curve Discrete Logarithm Problem is a discrete logarithm problem on an elliptic curve), the essence of which is to find an integer k from known points P and Q = k * P , is difficult to solve. In addition to the equation, an important parameter of the curve is the base (generating) point G , which is selected for each curve separately. The secret key in accordance with the EC technology is a large random number k , and the reported public key is the product of k by the base point G.

The correctness of the algorithm is significantly affected by the correct choice of both the curve itself (a, b , p coefficients) and the base point G.

Not every curve provides the required cryptographic strength, and for some of them the ECDLP task is solved quite effectively. Since an unsuccessful choice of a curve may lead to a decrease in the level of security provided, standardization organizations select entire blocks of curves that possess the necessary reliability. The use of standardized curves is also recommended because better compatibility between different implementations of information security protocols becomes possible.

The choice of a base point is determined by the consideration that its order is sufficiently large 2254 < q <2256. A point P ∈ E is called a point of order q if qP = I.

On elliptic curves, an algorithm for checking the EDS GOST R 34.10 - 2001 is built, which is currently the standard of the Russian Federation in the field of EDS. The scheme of this algorithm is shown in Fig. 4.4.

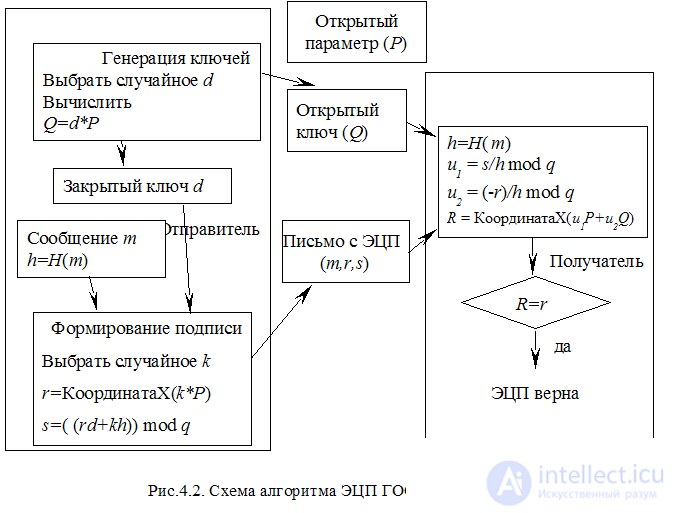
The main advantage of EC-based cryptosystems is that they provide reliability adequate to classical cryptosystems (RSA, ElGemal) on keys that are significantly shorter in length, which positively affects the encoding and decoding times. Digital signature cryptosystems based on elliptic curves with a key length of 160 bits have the same durability with DSA and El-Gamal cryptosystems with a key length of 1024 bits. It is expected that in the near future, these systems will occupy a dominant position in public-key cryptography. However, this will lead to more serious studies of the properties of these cryptoalgorithms, which may lead to the emergence of new, more efficient algorithms for solving the problem of the discrete logarithm in the group of points of elliptic curves.

Another approach to the formation of EDS is the use of symmetric encryption algorithms. However, currently known algorithms of this class are more likely to be of theoretical interest, since the efficiency of their implementation in terms of time or the amount of required calculations is very low. For example, the digital signature system proposed by Diffi and Helman on a symmetric cipher allows you to sign only one bit of information, which in practice will require the formation of a separate signature for each bit of the message being transmitted, and the signature of the bit has the size of the key of the block cipher, and each new bit requires the generation of its signature key. Therefore, systems of this class have not yet found wide application.

Conclusion.

Electronic digital signature is an effective means of protecting information from modification, which transfers the properties of a real signature under a document to the field of electronic document circulation. The digital signature is based on cryptographic methods such as asymmetric encryption and hash functions.