Lecture
A public-key cryptographic system (or asymmetric encryption , asymmetric cipher ) is an encryption and / or electronic signature (ES) system in which the public key is transmitted over an open (i.e., unprotected, available for observation) channel and is used to check the ES and encrypt messages. To generate electronic signature and to decrypt the message, use the private key [1]. Public key cryptographic systems are now widely used in various network protocols, in particular, in TLS protocols and its predecessor SSL (underlying HTTPS) in SSH. Also used in PGP, S / MIME.
The idea of public-key cryptography is very closely related to the idea of one-way functions, that is, such functions 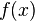 what is known
what is known 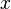 quite easy to find value
quite easy to find value 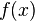 , while the definition
, while the definition 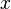 of
of 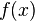 impossible for a reasonable time.
impossible for a reasonable time.
But the one-way function itself is useless in its application: it can encrypt a message, but it cannot be decrypted. Therefore, public key cryptography uses one-way functions with a loophole. A loophole is a secret that helps to decipher. That is, there is such 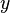 that knowing
that knowing 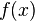 and
and 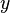 can calculate
can calculate 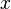 . For example, if you disassemble a clock into many parts, it is very difficult to assemble again working hours. But if there is an assembly instruction (loophole), then this problem can be easily solved.
. For example, if you disassemble a clock into many parts, it is very difficult to assemble again working hours. But if there is an assembly instruction (loophole), then this problem can be easily solved.
The following example helps to understand the ideas and methods of public-key cryptography - storing passwords in a computer. Every user on the network has a password. When entering, he specifies a name and enters a secret password. But if you store the password on a computer disk, then someone can read it (it is especially easy to do it for the administrator of this computer) and get access to secret information. To solve the problem, a one-way function is used. When creating a secret password in a computer, it is not the password itself that is saved, but the result of the calculation of the function from this password and user name. For example, user Alice came up with the password "Gladiolus". When saving this data, the result of the function is calculated. 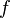 ( ALISA_GLADIOLUS ), let the result be the Daisy string, which will be stored in the system. As a result, the password file will look as follows:
( ALISA_GLADIOLUS ), let the result be the Daisy string, which will be stored in the system. As a result, the password file will look as follows:
| Name | 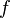 (Name: Password) (Name: Password) |
|---|---|
| ALICE | CHAMOMILE |
| BEAN | NARCISSUS |
Login now looks like this:
| Name: | ALICE |
|---|---|
| Password: | GLADIOLUS |
When Alice enters a “secret” password, the computer checks whether or not the function applied to ALISA_GLADIOL gives the correct result CAMOMILE stored on the computer disk. It is necessary to change at least one letter in the name or in the password, and the result of the function will be completely different. The “secret” password is not stored in the computer in any way. The password file can now be viewed by other users without losing privacy, since the function is almost irreversible.
In the previous example, a one-way function is used without a loophole, since it is not required to receive the original one using an encrypted message. The following example considers a scheme with the ability to restore the original message using a "loophole", that is, inaccessible information. To encrypt text, you can take a large subscriber directory, consisting of several thick volumes (it is very easy to find the number of any resident of the city, but it is almost impossible to find a subscriber by a known number). For each letter from the encrypted message is selected a name that starts with the same letter. Thus, the letter is assigned to the telephone number of the subscriber. The message sent, for example " BOX ", will be encrypted as follows:
| Message | Selected name | Cryptotext |
|---|---|---|
| TO | Korolev | 5643452 |
| ABOUT | Nuts | 3572651 |
| R | Ruzaeva | 4673956 |
| O | Osipov | 3517289 |
| B | Baturin | 7755628 |
| TO | Kirsanova | 1235267 |
| BUT | Arsenyev | 8492746 |
The cryptotext will be a chain of numbers recorded in the order of their selection in the directory. To make it difficult to decipher, you should choose random names that begin with the desired letter. Thus, the original message can be encrypted with many different lists of numbers (cryptotext).
Examples of such cryptotext:
| Cryptotext 1 | Cryptotext 2 | Cryptotext 3 |
|---|---|---|
| 1235267 | 5643452 | 1235267 |
| 3572651 | 3517289 | 3517289 |
| 4673956 | 4673956 | 4673956 |
| 3517289 | 3572651 | 3572651 |
| 7755628 | 7755628 | 7755628 |
| 5643452 | 1235267 | 5643452 |
| 8492746 | 8492746 | 8492746 |
To decipher the text, you must have a directory, compiled according to the increase of numbers. This handbook is a loophole (a secret that helps get the initial text), known only to legal users. Without a copy of the directory, the cryptanalyst will spend a lot of time decrypting. [2]
Let be 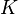 - key space, and
- key space, and  and
and 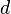 - encryption and decryption keys, respectively.
- encryption and decryption keys, respectively. 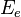 - encryption function for an arbitrary key
- encryption function for an arbitrary key 
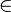
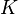 such that:
such that:
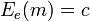
Here 
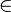
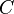 where
where 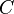 - space of ciphertexts, and
- space of ciphertexts, and 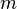
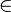
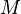 where
where 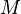 - message space.
- message space.
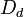 - the decryption function, with which you can find the original message
- the decryption function, with which you can find the original message 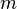 knowing ciphertext
knowing ciphertext  :
:
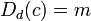
{ 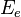 :
: 
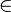
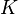 } Is the encryption set, and {
} Is the encryption set, and { 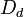 :
: 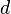
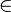
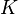 } Is the appropriate decryption set. Each pair
} Is the appropriate decryption set. Each pair 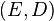 has the property: knowing
has the property: knowing 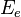 impossible to solve the equation
impossible to solve the equation 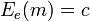 that is, for a given arbitrary ciphertext
that is, for a given arbitrary ciphertext 
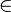
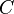 , unable to find message
, unable to find message 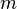
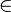
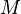 . This means that by this
. This means that by this  unable to determine appropriate decryption key
unable to determine appropriate decryption key 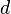 .
. 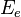 is a one-way function, but
is a one-way function, but 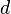 - eyelet. [3]
- eyelet. [3]
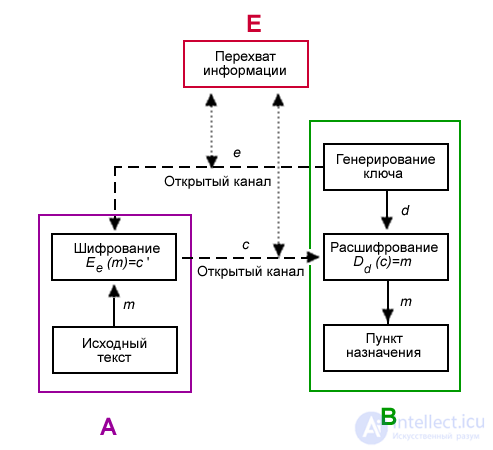
Below is a diagram of the transfer of information by person A to person B. They can be both individuals and organizations, and so on. But for easier perception, it is common practice to identify participants with people, most commonly referred to as Alice and Bob. The participant who seeks to intercept and decipher the messages of Alice and Bob is most often called Eva.
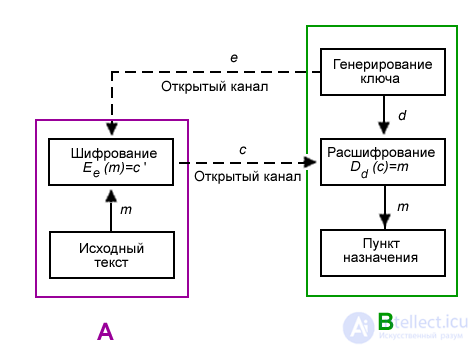
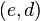 and sends the encryption key
and sends the encryption key  (public key) Alice through the open channel, and the decryption key
(public key) Alice through the open channel, and the decryption key 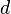 (private key) is protected and secret (it should not be transmitted over an open channel).
(private key) is protected and secret (it should not be transmitted over an open channel).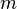 Bob, Alice uses a public key encryption function
Bob, Alice uses a public key encryption function  :
: 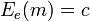 ,
,  - received ciphertext.
- received ciphertext. by applying the inverse transform
by applying the inverse transform 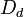 uniquely determined by value
uniquely determined by value 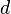 .
.The beginning of asymmetric ciphers was laid in the work “New Directions in Modern Cryptography” by Whitfield Diffie and Martin Hellman, published in 1976. Being influenced by the work of Ralph Merkle on the distribution of the public key, they proposed a method for obtaining the secret keys using a public channel. This method of exponential key exchange, which became known as Diffie-Hellman key exchange, was the first published practical method for establishing the separation of a secret key between authenticated channel users. In 2002, Hellman proposed to call this algorithm "Diffie - Hellman - Merkle", recognizing the contribution of Merkle to the invention of public key cryptography. The same scheme was developed by Malcolm Williamson in the 1970s, but kept secret until 1997. The Merkle method of public key distribution was invented in 1974 and published in 1978, it is also called the Merkle mystery.
In 1977, scientists Ronald Rivest, Adi Shamir and Leonard Adleman of the Massachusetts Institute of Technology developed an encryption algorithm based on a factoring problem. The system was named after the first letters of their surnames (RSA - Rivest, Shamir, Adleman). The same system was invented in 1973 by Clifford Cox (Eng. Clifford c *** ks ), who worked at the Government Communications Center (GCHQ), but this work was kept only in the internal documents of the center, so its existence was not known until 1977 . RSA was the first algorithm, suitable for both encryption and digital signature.
In general, the basis of known asymmetric cryptosystems is one of the complex mathematical problems, which allows one to construct one-way functions and loophole functions. For example, the Merkle-Hellman and Hora-Rivesta cryptosystems rely on the so-called backpack packing problem.
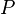 . It should be difficult to solve in the sense of a theory: there should not be an algorithm with which one could sort out all the solutions to the problem
. It should be difficult to solve in the sense of a theory: there should not be an algorithm with which one could sort out all the solutions to the problem 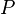 in polynomial time relative to the size of the problem. It is more correct to say: there should not be a known polynomial algorithm that solves this problem - since it has not yet been proved for any problem that there is no suitable algorithm for it in principle.
in polynomial time relative to the size of the problem. It is more correct to say: there should not be a known polynomial algorithm that solves this problem - since it has not yet been proved for any problem that there is no suitable algorithm for it in principle.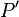 of
of 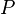 . It should be solved in polynomial time and better if linear.
. It should be solved in polynomial time and better if linear.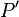 to get the task
to get the task 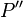 completely different from the original. Task
completely different from the original. Task 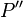 should at least look like the original intractable task
should at least look like the original intractable task 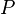 .
.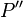 opens with a description of how it can be used as an encryption key. How of
opens with a description of how it can be used as an encryption key. How of 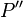 receive
receive 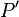 Kept secret as a secret loophole.
Kept secret as a secret loophole.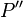 -problem, the first uses a secret loophole and solves
-problem, the first uses a secret loophole and solves 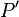 -task
-taskLet there be 3 keys 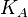 ,
, 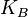 ,
, 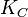 distributed as shown in the table.
distributed as shown in the table.
| Face | Key |
|---|---|
| Alice | 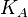 |
| Bean | 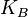 |
| Carol | 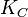 |
| Dave | 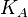 , , 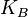 |
| Ellen | 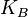 , , 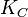 |
| Franc | 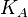 , , 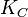 |
Then Alice can encrypt the message with a key. 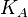 , and Ellen decrypt keys
, and Ellen decrypt keys 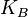 ,
, 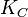 , Carol - encrypt key
, Carol - encrypt key 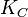 , and Dave decrypt the keys
, and Dave decrypt the keys 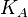 ,
, 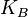 . If Dave encrypts the message with a key
. If Dave encrypts the message with a key 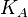 , the message will be able to read Ellen, if the key
, the message will be able to read Ellen, if the key 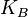 , then Frank will be able to read it, if with both keys
, then Frank will be able to read it, if with both keys 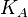 and
and 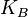 , the message will read Carol. By analogy, there are other participants. Thus, if one subset of keys is used for encryption, the remaining keys of the set are required for decryption. This scheme can be used for n keys.
, the message will read Carol. By analogy, there are other participants. Thus, if one subset of keys is used for encryption, the remaining keys of the set are required for decryption. This scheme can be used for n keys.
| Encrypted by key | Decrypted key |
|---|---|
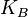 and and 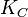 |
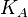 |
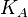 and and 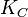 |
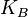 |
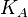 and and 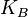 |
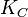 |
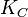 |
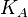 , , 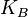 |
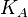 |
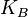 , , 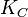 |
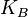 |
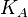 , , 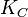 |
Consider first a set of three agents: Alice, Bob and Carol. Alice issued keys 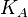 and
and 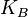 Bob -
Bob - 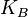 and
and 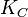 , Carol -
, Carol - 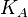 and
and 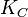 . Now, if the message being sent is encrypted with a key
. Now, if the message being sent is encrypted with a key 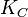 , then only Alice can read it, consistently applying keys
, then only Alice can read it, consistently applying keys 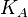 and
and 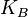 . If you want to send a message to Bob, the message is encrypted with a key.
. If you want to send a message to Bob, the message is encrypted with a key. 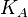 , Carol - key
, Carol - key 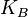 . If you want to send a message to both Alice and Carol, then keys are used for encryption.
. If you want to send a message to both Alice and Carol, then keys are used for encryption. 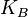 and
and 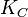 .
.
Преимущество этой схемы заключается в том, что для её реализации нужно только одно сообщение и n ключей (в схеме с n агентами). Если передаются индивидуальные сообщения, то есть используются отдельные ключи для каждого агента (всего n ключей) и каждого сообщения, то для передачи сообщений всем различным подмножествам требуется 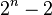 ключей.
ключей.
Недостатком такой схемы является то, что необходимо также широковещательно передавать подмножество агентов (список имён может быть внушительным), которым нужно передать сообщение. Иначе каждому из них придется перебирать все комбинации ключей в поисках подходящей. Также агентам придется хранить немалый объём информации о ключах.[4]
Казалось бы, что криптосистема с открытым ключом — идеальная система, не требующая безопасного канала для передачи ключа шифрования. Это подразумевало бы, что два легальных пользователя могли бы общаться по открытому каналу, не встречаясь, чтобы обменяться ключами. Unfortunately, this is not the case. Рисунок иллюстрирует, как Ева, выполняющая роль активного перехватчика, может захватить систему (расшифровать сообщение, предназначенное Бобу) без взламывания системы шифрования.
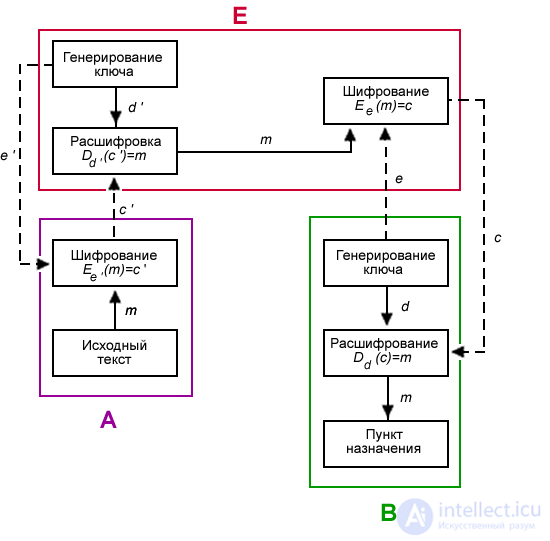
В этой модели Ева перехватывает открытый ключ  , посланный Бобом Алисе. Затем создает пару ключей
, посланный Бобом Алисе. Затем создает пару ключей 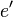 and
and 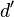 , «маскируется» под Боба, посылая Алисе открытый ключ
, «маскируется» под Боба, посылая Алисе открытый ключ 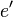 , который, как думает Алиса, открытый ключ, посланный ей Бобом. Ева перехватывает зашифрованные сообщения от Алисы к Бобу, расшифровывает их с помощью секретного ключа
, который, как думает Алиса, открытый ключ, посланный ей Бобом. Ева перехватывает зашифрованные сообщения от Алисы к Бобу, расшифровывает их с помощью секретного ключа 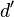 , заново зашифровывает открытым ключом
, заново зашифровывает открытым ключом  Боба и отправляет сообщение Бобу. Таким образом, никто из участников не догадывается, что есть третье лицо, которое может как просто перехватить сообщение
Боба и отправляет сообщение Бобу. Таким образом, никто из участников не догадывается, что есть третье лицо, которое может как просто перехватить сообщение 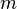 , так и подменить его на ложное сообщение
, так и подменить его на ложное сообщение 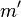 . Это подчеркивает необходимость аутентификации открытых ключей. Для этого обычно используютсертификаты. Распределённое управление ключами в PGP решает возникшую проблему с помощью поручителей.
. Это подчеркивает необходимость аутентификации открытых ключей. Для этого обычно используютсертификаты. Распределённое управление ключами в PGP решает возникшую проблему с помощью поручителей.
Ещё одна форма атаки — вычисление закрытого ключа, зная открытый (рисунок ниже). Криптоаналитик знает алгоритм шифрования 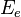 , анализируя его, пытается найти
, анализируя его, пытается найти 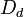 . Этот процесс упрощается, если криптоаналитик перехватил несколько криптотекстов с, посланных лицом A лицу B.
. Этот процесс упрощается, если криптоаналитик перехватил несколько криптотекстов с, посланных лицом A лицу B.
Большинство криптосистем с открытым ключом основаны на проблеме факторизации больших чисел. К примеру, RSA использует в качестве открытого ключа n произведение двух больших чисел. Сложность взлома такого алгоритма состоит в трудности разложения числа n на множители. Но эту задачу решить реально. И с каждым годом процесс разложения становится все быстрее. Ниже приведены данные разложения на множители с помощью алгоритма «Квадратичное решето».
| Year | Число десятичных разрядов в разложенном числе |
Во сколько раз сложнее разложить на множители 512-битовое число |
|---|---|---|
| 1983 | 71 | > 20 млн |
| 1985 | 80 | > 2 млн |
| 1988 | 90 | 250 тыс. |
| 1989 | 100 | 30 тыс. |
| 1993 | 120 | 500 |
| 1994 | 129 | 100 |
Также задачу разложения потенциально можно решить с помощью Алгоритма Шора при использовании достаточно мощного квантового компьютера.
Для многих методов несимметричного шифрования криптостойкость, полученная в результате криптоанализа, существенно отличается от величин, заявляемых разработчиками алгоритмов на основании теоретических оценок. Поэтому во многих странах вопрос применения алгоритмов шифрования данных находится в поле законодательного регулирования. В частности, в России к использованию в государственных и коммерческих организациях разрешены только те программные средства шифрования данных, которые прошли государственную сертификацию в административных органах, в частности, в ФСБ,ФСТЭК.[6]
Алгоритмы криптосистемы с открытым ключом можно использовать[7]
Преимущества асимметричных шифров перед симметричными:
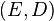 можно не менять значительное время (при симметричном шифровании необходимо обновлять ключ после каждого факта передачи).
можно не менять значительное время (при симметричном шифровании необходимо обновлять ключ после каждого факта передачи).Недостатки алгоритма несимметричного шифрования в сравнении с симметричным:
| Длина симметричного ключа, бит | Длина ключа RSA, бит |
|---|---|
| 56 | 384 |
| 64 | 512 |
| 80 | 768 |
| 112 | 1792 |
| 128 | 2304 |
Comments
To leave a comment
Information security, Cryptography and cryptanalysis, Steganography and Stegoanalysis
Terms: Information security, Cryptography and cryptanalysis, Steganography and Stegoanalysis