Cryptography and computer security (part 3)

Now we can complicate the cipher in a fundamentally different way. Instead of using a single lookup table, we can use several tables in a chaotic but predetermined order. The order of using the tables and forms the key. If we use only two tables, labeled 0 and 1, then the type key may be, for example, like this: 1101101. Now we are dealing with a multi-alphabet substitution. Regarding this new source of complexity in the cipher, the following question arises: is it possible to simplify the lookup tables by making them smaller? The simplest binary substitution that you can perform is replacing one binary digit with another, in which case there are only two different lookup tables. Let's look at these two tables, each of them will correspond to one of the two main types of key, as shown in the following illustration. The table labeled "Key 1" replaces zeros with ones and vice versa, while the table labeled "Key 0" leaves the digits unchanged. There are only two possibilities. But it turns out that the same effect can be obtained using an operation known as modulo-2 addition: two identical digits result in 0, two different digits - 1. Therefore, in this case, the wildcard key can also be called an additive key.

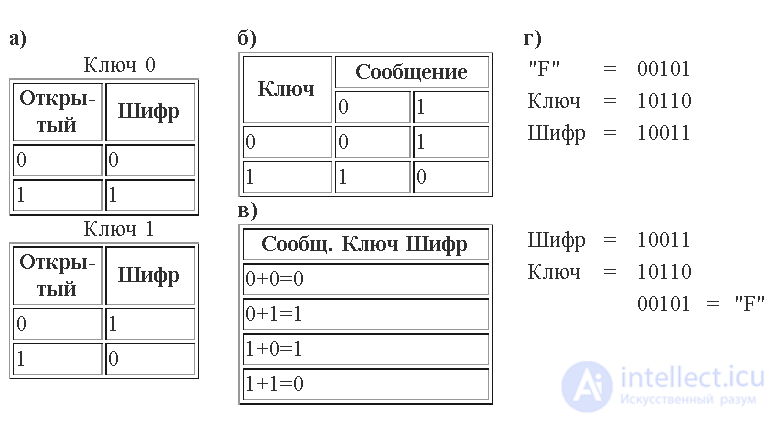
Binary substitution in its simplest form allows only two possibilities: (a) in one table (Key 0) open digits are equal to cipher digits, in the second (Key 1) cipher digits are opposite to open digits. In this variant of binary substitution, two substitution tables can be replaced with a single addition table modulo 2 (b); in this case, binary permutations are equivalent to binary addition (c). The encryption key for binary modulo 2 addition can be an arbitrary sequence of ones and zeros. To encrypt the binary representation of the letter of the message, add key digits to each digit of the message. When decrypting, numbers are subtracted (this is the same as modulo 2 addition).

Before proceeding further, let me explain that, starting from this point, we will tacitly assume that the message we want to cryptographically translate is first of all translated into a sequence of binary numbers. Any sort of information, whether it be letters, music or a television signal, can be represented in binary code. We will no longer worry about the original meaning of messages - we will only deal with their binary representation.

Now we are ready to consider what happens when we encrypt a sequence of binary digits, say, 0001010, converting it into another sequence using two keys, Key 1 and Key 0, in some arbitrary order: 1101101. Taking into account the rule that Key 1 replaces zeros On units and vice versa, and Key 0 leaves the numbers unchanged, we get the following: Message: 0001010
Key: + 1101101
Code: 1100111


This is modulo-2 addition. It has a convenient property — modulo-two subtraction is the same as addition, so the original message can be restored by simply adding a sequence of key digits (known to the one to whom the message is sent) to the sequence of cipher digits : Code: 1100111
Key: - 1101101
Message: 0001010


The question immediately arises: does the simple code considered have any practical significance? Since this cipher, in essence, uses only two minimum size lookup tables, it is obvious that we have to switch between them often, and do it randomly, that is, add a random sequence of key digits to the data. Suppose we do this. Then the answer to our question is rather unexpected: we have a potentially unbreakable cipher. From the point of view of information theory, this cipher does the following: one bit of information (or more precisely, disinformation!) Of a key is added to each bit of message information. This is enough to completely destroy any structure that the original message could have, if only the key digits are taken in a random, say, coin-flip order, and the key sequence is the same length as the message, and never repeats.

Why is this system really unexampled? In fact, it is not even a “system” at all. The considered cryptographic transformation is nothing more than the accidental addition of a single digit, and is equally trivial. Durability of the method follows solely from the fact that for each digit of the message we completely and randomly change the key. This is the only class of ciphers for which it is possible to prove the secrecy in the absolute sense of the word.

Even if the opponent attempts to open the system with brute force, for example, by testing all possible added keys (26 or 64, in the case of our 6-bit message), he will receive all possible open texts, including the one we actually encrypted. So, if we encrypted the name "Tom" (which would require at least fifteen binary digits), the analyst would find among his decryption options all English three-letter names, such as Joe, Jim, Jobe (Job ), and so on, including Tom (Tom), but no hints on which name is correct. Even a god or a devil who could test all possible keys in an instant could not introduce any certainty here. This system is well known and is used in practice under various names, such as the Vernam system or one-time notebook, by all major governments.

In real systems, two identical tapes with random key numbers are first prepared; tapes can be of any type - teletype, perforated, magnetic, or some other type. One remains with the sender, and the other is transmitted in a "non-intercepted" manner, for example, by courier with a guard, to the legal recipient. When the sender wants to send a message, he first converts it into binary form and places it in a device that adds two digits read from the key tape modulo each digit of the message, as shown in the following figure. On the receiving side, the encoded message is recorded and passed through a machine similar to the device used for encryption, which adds (subtracts) modulo two digits read from the key tape to each binary digit of the message, thus obtaining the plaintext. At the same time, of course, the key tape should move absolutely synchronously with its duplicate used for encryption.

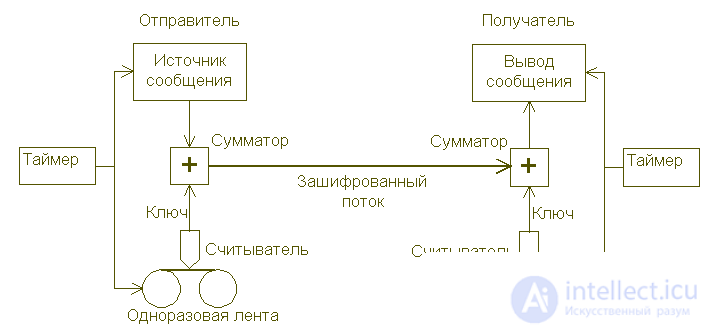
The “one-off tape” system requires that the transmitting and receiving sides have tapes with the same key, synchronized by means of a timer. Message digits and key numbers are added modulo 2, the resulting encrypted stream is transmitted through the communication channel, after which the key is subtracted from the data (added modulo 2). For high volume traffic, extensive stocks of key numbers must be delivered to the recipient in advance and stored with him.

The fundamental flaw in the Vernam system is that for each bit of information transmitted, the recipient needs to store one pre-prepared bit of key information. Moreover, these bits must be followed in a random sequence, and this sequence cannot be used again. If you need to encrypt high volume traffic, this is a pretty serious limitation. By virtue of this requirement, the Varnam system is only used to transmit the highest secrecy messages.

To circumvent the problem of pre-sending a large-volume secret key message to a recipient, engineers and inventors have come up with many ingenious schemes for generating very long streams of pseudo-random numbers from several short streams in accordance with some algorithm. The recipient of an encrypted message must be provided with exactly the same generator as the sender. Of course, such an algorithm involves the use of systematic procedures that add regularities to the ciphertext, the detection of which can help the analyst to decrypt the message.

One of the main methods of constructing such generators is to use two or more bit tapes, read from which the data are added bit by bit to obtain a "mixed" stream. For example, a simple disposable tape can be replaced by two cyclical tapes, the lengths of which are simple or mutually simple numbers. Since in this case the lengths of the tapes do not have common factors, the stream obtained from them has a repetition period equal to the product of their lengths: two tapes having a length of 1000 and 1001, respectively, result in a composite stream that does not repeat in the first 10001001 or 1001000 numbers. Tapes circulate through an adder that adds modulo the two digits read from them, as shown in the following figure. The output of the adder is the key used to encrypt the message. Therefore, it is important that the composite stream exceeds the length of all the messages taken together, which can be transmitted within a reasonable period of time.

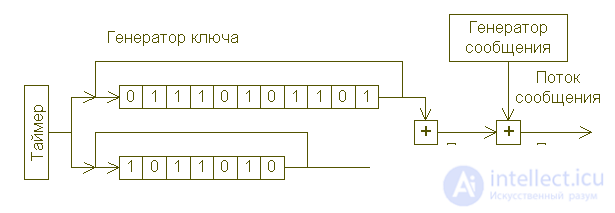
The pseudo-random tape system uses two closed sections of the tape with key numbers or bits that are added to each other in order to obtain a pseudo-random key bit stream added in succession to the message bits exactly the same as when using a disposable tape. Decryption is performed using a key that is generated in the same way on the receiver. Thus, several short tapes replace one long one, but the resulting internal periodicities can help the analyst in opening the cipher.

Since the bitwise adder is a linear device, it is initially cryptographically weak, but can be amplified in many different ways. You can pile on complication by complication by introducing feedback chains, possibly related in some way to the message being transmitted, or by introducing non-linear mathematical operations such as substitutions in blocks of digits of a suitable size. The non-secret cryptographic literature contains many charming designs of pseudo-random sequence generators, all of which can be, in principle, reduced to the same basic scheme shown in the following figure. In one way or another, they generate pseudo-random numbers, performing complex mathematical operations on an orderly sequence of input numbers, thus transforming them in a way that the analyst is supposed to stump.

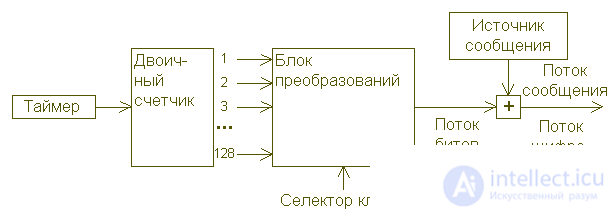
Pseudo-random flow can be obtained in a more complicated way. In this generalized representation of its generator, a binary counter provides input numbers with a transform block that generates keystream digits that are added further to the flow of digits of the message.