Cryptography and computer security (part 2)

The reader may be surprised and discouraged by the fact that the Vernama cipher class — the only cipher class for which non-secrecy can be proved in the absolute sense of the term — is imperfect in another sense: it alone does not provide protection against skillful traffic fraud. not redundant.

Regardless of whether the message is encoded using true random numbers or a pseudo-random sequence of numbers, in a similar bit-by-bit encryption, a single error that occurred during the transmission of the message remains within one numeric position; the error does not "multiply", does not apply to the rest of the message. This cipher does not introduce intersymbol dependencies. When a message is written in a natural language, such as English, the context of natural redundancy allows the person reading the text to easily detect random errors. So, if some of the 5 bits representing the letter E were distorted in such a way that the corresponding group of bits became a representation of the letter F (so for example that the word SECRET turned into SECRFT), then the human reader would immediately detect the error.

A completely different situation when using computers. The transmitted data here may not contain redundancy, for example, if they are completely numeric, and in this situation an error in just one digit can cause a whole cascade of computational errors. The study of the problem showed that simple error detection codes are not suitable for protecting the integrity of computer data from possible frauds by human experts. In this situation, it is necessary not only to detect errors, but authentication protected by cryptographic methods. It was unexpectedly found that this is best achieved if the decision is based on certain principles that are intrinsic to encryption structures. Instead of trying to change the concept of a stream, let's take a fresh look at the concept of all cryptography: replacing blocks or digits of a message.

We will call any cipher that converts n digits of a message to n digits of a cipher block cipher. For example, a block will be a cipher that converts code 00000, which by our agreement represents the letter A in plaintext, say, 11001, the equivalent of A for the ciphertext, using a certain permutation key, exactly as the lookup table specifies. To see how such a binary transformation is performed by an electronic device, let's consider substitutions only in groups of three binary digits, as shown in the following figure.

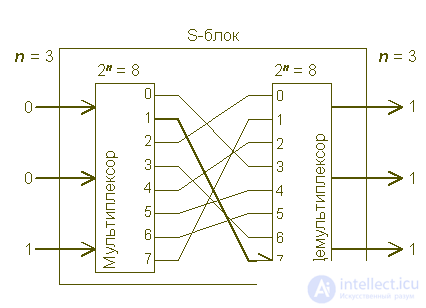
The substitution block, unlike streaming devices, is more general in nature and includes both linear and nonlinear transformations: it does not just add zeros and ones to the input digits, but can replace any input block of digits with any output block. In reality, it consists of two switches - one converts a binary number of n digits into one digit at the base of 2n, the other performs the inverse transform. The block thus contains 2n internal switch connections that can be made 2n! different ways. This means that in the case of the block with n = 3 shown in this figure, there are 40,320 different layout options or tables similar to the one shown in the figure. A block of this type with n = 128 would make the analysis practically impracticable, but it is technologically impossible to create.

With the help of three binary digits, eight elements can be represented: 23 is eight. The device performing the substitution consists of two switches. The first converts a sequence of three binary digits into the corresponding octal value, sending a signal to exactly one of the eight output lines. These eight outputs can be connected to the eight inputs of the second switch by any of the 8! or 40,320 ways. We are free to choose which of the 40,320 different options for connecting or switching wires between the first and second switches to use. The role of the second switch is to convert the input, represented by a single digit in base 8, back to a three-digit binary output.

If the substitution device were built to process a five-digit binary input, it could be used to encrypt an alphabet of 32 characters. The number of possible connections of the two switches would then be 32 !. This might seem like an incredibly large number of keys, but the cipher created in this way still needs to be treated as very weak: it cannot withstand frequency analysis. This weakness is not its inherent property; From the mathematical point of view, the described device determines the most common possible transformation. It includes, for any given size of input / output, any possible reversible cipher that has ever been, or even just could have been invented; mathematicians might say that it represents a complete symmetric group. It is completely “non-systematic”: a single switch mix says nothing to an opponent regarding all other joints. Weakness is not an intrinsic property of this cipher, it is due to the selected block size. Despite the large number of keys, the “catalog” of possible inputs or outputs is very small: there are only 32 elements in it. What is needed here is such a large catalog so that for any opponent it would be practically impossible to write it down. If we, for example, had a block with 128 inputs and outputs, the analyst would have to overcome 2128 (or more than 1038) possible blocks of digits — such a huge number that the frequency analysis here is simply not feasible. Unfortunately, the 128-input permutation device would also require 2128 internal connections between the first and second switches, which is technologically unrealizable. This is the fundamental dilemma of cryptography. We know what is ideal, but we cannot achieve it in practice.

However, there is a transformation that is easy to implement for a large set of inputs. It is practically possible, for example, to build a unit with, say, 128 input and output pins, which are internally connected by conventional wires, as shown in the following figure. For such a "permutation block" with n outputs there is n! possible options for switching wires, each of which is determined by a separate key. It can easily be built for n = 128. Although this will provide us with a large number of possible keys (128!), Which is quite useful, we will now face a new difficulty. By using a set of specially designed messages, it is possible to completely determine the key of such a system in just n-1 (in this case 127) attempts. This technique is to use a series of messages containing one single unit in n-1 different positions; the position of the unit in the output block will "give out" the wire connection used in the device. The weakness of the simple permutation block is that it is again a linear system.

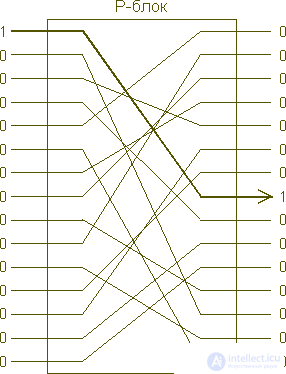
The permutation block can "serve" a lot of lines, but it only changes the position of the numbers. The opponent can recognize his internal switching by supplying single units to the input and observing at which output these units appear.

We need a compromise that would at least approach the overall system in terms of performance. We came to the idea of ​​a composite cipher, in which two or more ciphers are combined in such a way that the resulting system is more resistant than each of its individual systems. Just before World War I, various cumbersome ciphers using several encryption steps were investigated. The first truly successful model was probably the system invented by the Germans, known as the ADFCVX system. We need to note here only that it connected "crushing" with "permutations". In this procedure, the message was divided into segments and these segments were rearranged to other places. An important fact to be noted is that the composite cipher made up of block ciphers is again a block cipher; The goal here, of course, is that the cipher behaves as far as possible, like the common replacement cipher.

Between the first and second world wars, interest in composite ciphers has almost completely disappeared due to the successful development of rotary or wire-disk machines that belong to the general class of pseudo-random sequence generators. A typical rotary machine had a keyboard resembling a typewriter keyboard. Each letter was encrypted using several disks working in a certain sequence; for the next letter to be encrypted, the disks were transferred to a different position using an irregular and key-dependent algorithm. The message was decrypted by an identical machine with the exact same key set.

Modern interest in composite ciphers has arisen due to an article by Claude Shannon entitled "Communication Theory in Secret Systems", which was published in the technical journal of Bell (Bell System Technical Journal) in 1949. In the section on the practical development of ciphers, Shannon introduced the concept of "mixing transformation", which implies a special way of using the results of transformation. In addition to the presentation of intuitive principles, leading, he believed, to the creation of strong ciphers, he introduced the concepts of "mixing" and "dispersion". His article opened up virtually unlimited possibilities for the development and research of ciphers.

The way in which the principles of mixing and scattering should be combined to obtain cryptographic robustness can be described as follows: We have seen that general-purpose permutations cannot be implemented for large values ​​of n, say, for n = 128, and therefore we should confine ourselves to substitution schemes, have a practical size. In the system developed by IBM and called "Lucifer", we chose n = 4 for substitution blocks. Although it may seem like a small number, such substitution can be quite effective if the substitution key, or the switching circuit of conductors, is right. In Lucifer, a non-linear substitution effectively provides a certain degree of mixing.

We also saw that a linear permutation block is easy to build, even for n = 128. The number of input and output terminals is n. Being a "shuffler" of numbers in its pure form, a device that simply moves numbers from place to place without changing the number of ones and zeros, the permutation block is a natural mixing distributor, so it can provide optimal dispersion.