Lecture
Quantum cryptography is a method of protecting communications based on the principles of quantum physics. Unlike traditional cryptography, which uses mathematical methods to ensure the secrecy of information, quantum cryptography focuses on physics, considering the cases when information is transferred using objects of quantum mechanics. The process of sending and receiving information is always carried out by physical means, for example, using electrons in an electric current, or photons in fiber-optic communication lines. Eavesdropping can be viewed as a change in certain parameters of physical objects — in this case, carriers of information.
The technology of quantum cryptography is based on the fundamental uncertainty of the behavior of the quantum system, expressed in Heisenberg's principle of uncertainty - it is impossible to simultaneously obtain the coordinates and momentum of a particle, it is impossible to measure one photon parameter without distorting the other.
Using quantum phenomena, one can design and create a communication system that can always detect eavesdropping. This is ensured by the fact that an attempt to measure the interconnected parameters in a quantum system introduces violations in it, destroying the original signals, which means that legitimate users can recognize the degree of activity of the interceptor by the noise level in the channel.
For the first time, the idea of protecting information using quantum objects was proposed by Steven Wiesner in 1970. A decade later, Charles Bennett (IBM) and Gilles Brassard (University of Montreal), familiar with the work of Wisner, offered to transmit a secret key using quantum objects. In 1984, they assumed the possibility of creating a fundamentally protected channel using quantum states. After that, they proposed a scheme (BB84) in which legal users (Alice and Bob) exchange messages, presented in the form of polarized photons, over a quantum channel.
An attacker (Eve) trying to investigate the transmitted data cannot measure photons without distorting the message text. Legal users of the open channel compare and discuss the signals transmitted through the quantum channel, thereby checking them for the possibility of interception. If they do not reveal any errors, the transmitted information can be considered randomly distributed, random and secret, despite all the technical capabilities that the cryptanalyst can use.
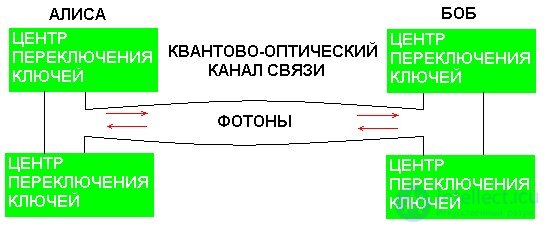
The first working quantum cryptographic scheme was built in 1989 at the IBM Bennett and Brassard Research Center of IBM. This scheme was a quantum channel, at one end of which was Alice’s transmitting apparatus, and Bob’s receiving apparatus at the other. Both devices are placed on an optical bench about 1 m long, in an opaque casing with dimensions of 1.5 × 0.5 × 0.5 m. The control was carried out with the help of a computer loaded with software representations of legal users and an intruder.
The integrity of the transmitted data is directly dependent on the intensity of the flashes of light used for transmission. Weak flashes, although making it difficult to intercept messages, still lead to an increase in the number of errors in a legitimate user, when measuring the correct polarization. Increasing the intensity of flares greatly simplifies interception by splitting the initial single photon (or a beam of light) into two: the first is still directed to the legal user, and the second is analyzed by the attacker. Legal users can correct errors using special codes, discussing the coding results on an open channel.
But still, with this, some of the information gets to the cryptanalyst. Nevertheless, legal users of Alice and Bob, studying the number of detected and corrected errors, as well as the intensity of flashes of light, can give an estimate of the amount of information that came to the attacker.
Scheme BB84 works as follows. First, the sender (Alice) generates photons with random polarization selected from 0, 45, 90 and 135 °. The recipient (Bob) accepts these photons, then for each one selects randomly the method of measuring polarization, diagonal or perpendicular. Then, via an open channel, it reports on which method it has chosen for each photon, without disclosing the measurement results themselves. After that, Alice reports on the same open channel whether the correct type of measurement was chosen for each photon. Next, Alice and Bob discard those cases where Bob's measurements were incorrect. If there was no interception of a quantum channel, then the remaining information or key will be the remaining types of polarization. The output will be a sequence of bits: photons with horizontal or 45 ° polarization are assumed to be binary "0", and with vertical or 135 ° polarization - to binary "1". This stage of the quantum-cryptographic system is called the primary quantum transfer.
Alice sends photons having one of four possible polarizations, which she chooses randomly.
For each photon, Bob randomly chooses the type of measurement: it changes either the rectilinear polarization (+) or the diagonal (x).
Bob records the results of the change and keeps it secret.
Bob openly announces what type of measurements he took, and Alice tells him which measurements were correct.
Alice and Bob retain all the data received when Bob applied the correct measurement. This data is then translated into bits (0 and 1), the sequence of which is the result of the initial quantum transmission.
The next step is very important to evaluate attempts to intercept information in a quantum-cryptographic communication channel. This is done on the open channel by Alice and Bob by comparing and discarding the subsets of the obtained data randomly selected by them. If, after such a comparison, interception is detected, then Alice and Bob will have to discard all of their data and begin rerunning the primary quantum transmission. Otherwise, they leave the same polarization. According to the uncertainty principle, a cryptanalyst (Eve) cannot measure both the diagonal and rectangular polarization of the same photon. Even if they measure for any photon and then the same photon will be sent to Bob, then the number of errors will increase significantly, and this will become noticeable to Alice. This will lead to the fact that Alice and Bob will be completely confident in the interception of photons. If there is no discrepancy, the bits used for the comparison are discarded, the key is accepted. With probability 1 - 2 -k (where k is the number of bits compared), the channel was not tapped.
If the ill-wisher can not only listen to the main channel “Alice → Bob”, but also can falsify the work of the open channel Bob-> Alice, then the whole scheme collapses (Man-In-The-Middle).
The described algorithm is called the BB84 quantum key distribution protocol. In it, the information is encoded into orthogonal quantum states. In addition to using orthogonal states to encode information, non-orthogonal states can also be used (for example, the B92 protocol).
In 1991, Charles Bennett proposed the following algorithm for detecting distortions in the data transmitted over the quantum channel:
Consider the scheme of the physical implementation of quantum cryptography [1] . On the left is the sender, on the right - the recipient. In order for the transmitter to have the opportunity to vary the polarization of the quantum flux in pulses, and the receiver can analyze the polarization pulses, Pokel cells are used. The transmitter forms one of the four possible polarization states. Cell data is received in the form of control signals. Fiber is usually used to organize the communication channel, and a laser is taken as the light source.
On the recipient side, after the Pokel cell, there is a calcite prism, which should split the beam into two components, trapped by two photodetectors (PMT), and these in turn measure the orthogonal polarization components. First, it is necessary to solve the problem of the intensity of the transmitted quanta pulses arising during their formation. If the pulse contains 1000 quanta, there is a probability that 100 of them will be allotted by the cryptanalyst to their receiver. After that, conducting an analysis of open negotiations, he will be able to get all the data he needs. From this it follows that the ideal option is when the number of quanta in an impulse tends to one. Then any attempt to intercept part of the quanta will inevitably change the state of the entire system and, accordingly, will provoke an increase in the number of errors in the recipient. In this situation, you should not consider the received data, and re-transmit. However, when trying to make the channel more reliable, the sensitivity of the receiver rises to a maximum, and the specialists are faced with the problem of "dark" noise. This means that the recipient receives a signal that was not sent by the sender. In order for the data transmission to be reliable, the logical zeros and ones that make up the binary representation of the transmitted message are represented in the form of not one, but a sequence of states, which makes it possible to correct single and even multiple errors.
To further increase the fault tolerance of the quantum cryptosystem, the Einstein-Podolsky-Rosen effect is used, which arises when two photons are emitted in opposite directions by a spherical atom. The initial polarization of photons is not determined, but due to the symmetry of their polarization is always opposite. This determines the fact that the polarization of photons can be found only after measurement. A crypto scheme based on the Einstein-Podolsky-Rosen effect, guaranteeing the safety of the shipment, was proposed by Eckert. The sender generates several photon pairs, after which he defers one photon from each pair to itself, and sends the second one to the addressee. Then, if the registration efficiency is about one and the sender has a photon with polarization “1” on its hands, then the recipient will have a photon polarized “0” and vice versa. That is, legal users always have the opportunity to get the same pseudo-random sequences. But in practice it turns out that the efficiency of recording and measuring the polarization of a photon is very small.
In 1989, Bennett and Brassard at IBM Research Center built the first working quantum-cryptographic system. It consisted of a quantum channel containing an Alice transmitter at one end and a Bob receiver at the other, placed on an optical bench about a meter long in an opaque one-and-a-half meter casing measuring 0.5 × 0.5 m. The quantum channel itself was a free air channel about 32 The layout was controlled from a personal computer that contained a programmatic representation of the users of Alice and Bob, as well as the attacker. In the same year, the transmission of a message through a stream of photons through the air at a distance of 32 cm from computer to computer was completed successfully. The main problem with increasing the distance between the receiver and transmitter is the preservation of photon polarization. The reliability of the method is based on this.
Established with the participation of the University of Geneva, GAP-Optique, under the leadership of Nicholas Gisin, combines theoretical research with practical activities. The first result of these studies was the implementation of a quantum communication channel using a fiber optic cable 23 km long, laid across the bottom of the lake and connecting Geneva and Nyon. Then a secret key was generated, the error level of which did not exceed 1.4%. But still a huge disadvantage of this scheme was the extremely low speed of information transfer. Later, the specialists of this company managed to transfer the key to a distance of 67 km from Geneva to Lausanne with the help of an almost industrial design of equipment. But this record was broken by Mitsubishi Electric Corporation, which transmitted a quantum key to a distance of 87 km, however, at a speed of one byte per second.
IBM, GAP-Optique, Mitsubishi, Toshiba, Los Alamos National Laboratory, Caltech, a young company MagiQ and QinetiQ holding, supported by the British Department of Defense, are active in the field of quantum cryptography. In particular, an experimental communication line, about 48 kilometers long, was developed and began to be widely used in the Los Alamos national laboratory. Where, based on the principles of quantum cryptography, key distribution takes place, and the speed of distribution can reach several tens of kbps.
In 2001, Andrew Shields and his colleagues at TREL and the University of Cambridge created a diode capable of emitting single photons. The basis of the new LED is a “quantum dot” - a miniature piece of semiconductor material with a diameter of 15 nm and a thickness of 5 nm, which can capture only one pair of electrons and holes when current is applied to it. This made it possible to transmit polarized photons to a greater distance. During the experimental demonstration, it was possible to transmit encrypted data at a speed of 75 Kbps - despite the fact that more than half of the photons were lost.
The University of Oxford is tasked with increasing data transfer speeds. Quantum-cryptographic circuits are created using quantum amplifiers. Their use helps to overcome the speed limit in the quantum channel and, as a result, expanding the field of practical application of such systems.
At Johns Hopkins University, a 1 km-long quantum channel has a computer network, which automatically adjusts every 10 minutes. As a result, the error level is reduced to 0.5% at a communication speed of 5 kbps.
The UK Department of Defense maintains the QinetiQ research corporation, which is part of the former British DERA (Defense Evaluation and Research Agency), which specializes in non-nuclear defense research and is actively improving quantum encryption technology.
Research in the field of quantum cryptography is engaged in the American company Magiq Technologies from New York, which released the prototype of its own commercially developed quantum cryptotechnology. The main product of Magiq is the key distribution tool (quantum key distribution, QKD), which is called Navajo (after the name of the Navajo Indian tribe, whose language the Americans used to transmit secret messages during World War II, since no one knew it outside the United States). Navajo is capable of generating and distributing keys in real time using quantum technology tools and is designed to provide protection against internal and external intruders.
В октябре 2007 года на выборах в Швейцарии были повсеместно использованы квантовые сети, начиная избирательными участками и заканчивая датацентром ЦИК. Была использована техника, которую ещё в середине 90-х в Университете Женевы разработал профессор Николя Жизен. Также одним из участников создания такой системы была компания Id Quantique.
В 2011 году в Токио прошла демонстрация проекта «Tokyo QKD Network», в ходе которого разрабатывается квантовое шифрование телекоммуникационных сетей. Была проведена пробная телеконференция на расстоянии в 45 км. Связь в системе идёт по обычным оптоволоконным линиям. В будущем предполагается применение для мобильной связи.
Широкое распространение и развитие квантовой криптографии не могло не спровоцировать появление квантового криптоанализа, который обладает неоспоримыми преимуществами и экспоненциально перед обычным. Рассмотрим, например, всемирно известный и распространенный в наши дни алгоритм шифрования RSA (1977). В основе этого шифра лежит идея того, что на простых компьютерах невозможно решить задачу разложения очень большого числа на простые множители, ведь данная операция потребует астрономического времени и экспоненциально большого числа действий. Другие теоретико-числовые методы криптографии могут быть основаны на проблеме дискретного логарифмирования. Для решения этих двух проблем был разработан квантовый алгоритм Шора (1994), позволяющий найти за конечное и приемлемое время все простые множители больших чисел или решить задачу логарифмирования, и, как следствие, взломать шифры RSA и ECC. Поэтому создание достаточно крупной квантовой криптоаналитической системы является плохой новостью для RSA и некоторых других асимметричных систем. Необходимо только создание квантового компьютера, способного развить достаточную мощность.
По состоянию на 2012 год наиболее продвинутые квантовые компьютеры смогли разложить на множители числа 15 [2] (в 150 тыс. попыток верный ответ был получен в половине случаев, в соответствии с алгоритмом Шора [3] ) и 21.
В 2010 году учёные успешно опробовали [4] [5] один из возможных способов атаки, показав принципиальную уязвимость двух реализаций криптографических систем, разработанных компаниями ID Quantique и MagiQ Technologies [6] . И уже в 2011 году работоспособность метода была проверена в реальных условиях эксплуатации, на развёрнутой в Национальном университете Сингапура системе распространения ключей, которая связывает разные здания отрезком оптоволокна длиной в 290 м.
В эксперименте использовалась физическая уязвимость четырёх однофотонных детекторов (лавинных фотодиодов), установленных на стороне получателя (Боба). При нормальной работе фотодиода приход фотона вызывает образование электронно-дырочной пары, после чего возникает лавина, а результирующий выброс тока регистрируется компаратором и формирователем импульсов. Лавинный ток «подпитывается» зарядом, хранимым небольшой ёмкостью (≈ 1,2 пФ), и схеме, обнаружившей одиночный фотон, требуется некоторое время на восстановление (~ 1 мкс).
Если на фотодиод подавать такой поток излучения, когда полная перезарядка в коротких промежутках между отдельными фотонами будет невозможна, амплитуда импульса от одиночных квантов света может оказаться ниже порога срабатывания компаратора.
В условиях постоянной засветки лавинные фотодиоды переходят в «классический» режим работы и выдают фототок, пропорциональный мощности падающего излучения. Поступление на такой фотодиод светового импульса с достаточно большой мощностью, превышающей некое пороговое значение, вызовет выброс тока, имитирующий сигнал от одиночного фотона. Это и позволяет криптоаналитику (Еве) манипулировать результатами измерений, выполненных Бобом: она «ослепляет» все его детекторы с помощью лазерного диода, который работает в непрерывном режиме и испускает свет с круговой поляризацией, и по мере надобности добавляет к этому линейно поляризованные импульсы. При использовании четырёх разных лазерных диодов, отвечающих за все возможные типы поляризации (вертикальную, горизонтальную, ±45˚), Ева может искусственно генерировать сигнал в любом выбранном ею детекторе Боба.
Опыты показали, что схема взлома работает очень надёжно и даёт Еве прекрасную возможность получить точную копию ключа, переданного Бобу. Частота появления ошибок, обусловленных неидеальными параметрами оборудования, оставалась на уровне, который считается «безопасным».
Однако, устранить такую уязвимость системы распространения ключей довольно легко. Можно, к примеру, установить перед детекторами Боба источник одиночных фотонов и, включая его в случайные моменты времени, проверять, реагируют ли лавинные фотодиоды на отдельные кванты света.
Практически все квантово-оптические криптографические системы сложны в управлении и с каждой стороны канала связи требуют постоянной подстройки. На выходе канала возникают беспорядочные колебания поляризации ввиду воздействия внешней среды и двойного лучепреломления в оптоволокне. Но недавно [ когда? ] была сконструирована [ кем? ]such an implementation of the system, which can be called plug and play (“connect and work”). For such a system does not need adjustment, but only synchronization. The system is based on the use of the Faraday mirror, which allows to avoid double refraction and as a result does not require polarization adjustment. This allows you to send cryptographic keys on conventional telecommunications communication systems. To create a channel, you just need to connect the receiving and transmitting modules, synchronize and you can start the transfer. Therefore, such a system can be called plug and play.
Сейчас одним из самых важных достижений в области квантовой криптографии является то, что ученые смогли показать возможность передачи данных по квантовому каналу со скоростью до единиц Мбит/с. Это стало возможно благодаря технологии разделения каналов связи по длинам волн и их единовременного использования в общей среде. Что кстати позволяет одновременное использование как открытого, так и закрытого канала связи. Сейчас [ уточнить ] в одном оптическом волокне возможно создать около 50 каналов. Экспериментальные данные позволяют сделать прогноз на достижение лучших параметров в будущем:
At this stage, quantum cryptography is only approaching the practical level of use. The range of developers of quantum cryptography technologies covers not only the world's largest institutions, but also small companies that are just starting their activities. And all of them are already able to bring their projects from laboratories to the market. All this allows us to say that the market is at the initial stage of formation, when both can be represented on an equal footing.
Comments
To leave a comment
Information security, Cryptography and cryptanalysis, Steganography and Stegoanalysis
Terms: Information security, Cryptography and cryptanalysis, Steganography and Stegoanalysis