This series of articles describes a wave model of the brain that is seriously different from traditional models. I strongly recommend that those who have just joined begin reading from the first part.
The most simple to understand and simulate neural networks in which information is sequentially distributed from layer to layer. By applying a signal to the input, it is also possible to consistently calculate the state of each layer. These states can be interpreted as a set of descriptions of the input signal. Until the input signal changes, its description will remain unchanged.
A more complicated situation arises if we introduce feedback into the neural network. To calculate the state of such a network, one pass is no longer enough. As soon as we change the state of the network in accordance with the input signal, the feedback will change the input picture, which will require a new recalculation of the state of the entire network, and so on.
The ideology of the recurrent network depends on how the feedback delay and the interval of the change of images correlate. If the delay is much less than the shift interval, then we are most likely interested only in finite equilibrium states, and intermediate iterations should be perceived as an exclusively computational procedure. If they are comparable, then the network dynamics come to the fore.
F. Rosenblatt described cross-linked multilayer perceptrons and showed that they can be used to model selective attention and reproduce a sequence of reactions (Rosenblatt, Principles of Neurodynamic: Perceptrons and the Theory of Brain Mechanisms, 1962).
In 1982, John Hopfield proposed the design of a neural network with feedback such that its state can be determined based on the calculation of the minimum of the energy functional (Hopfield, 1982). It turned out that Hopfield networks have a remarkable property - they can be used as memory, addressed by content.
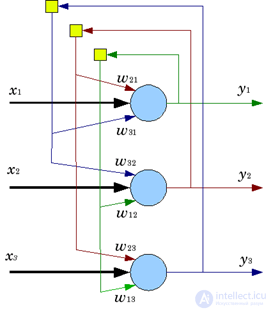 Hopfield network
Hopfield network Signals in the Hopfield network take spin values {-1,1}. Network learning is the memorization of multiple images.
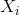
. Memorization takes place by adjusting the scales so that:
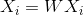
Which leads to an algorithm that allows us to determine network parameters with a simple non-iterative calculation:
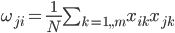
Where
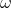
- a matrix made up of weights of neurons, and
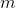
- the number of memorized images. Matrix diagonal
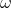
relies zero, which means the absence of the influence of neurons on themselves. The weights defined in this way determine the stable states of the network corresponding to the memorized vectors.
The activation function of the neurons is:
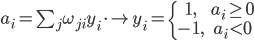
The input image is assigned to the network as an initial approximation. Then an iterative procedure begins, which, if lucky, converges to a steady state. Such a stable state, most likely, will be one of the memorized images. And it will be an image that is most similar to the input signal. In other words, the image is associated with it.
You can introduce the concept of network energy, like:
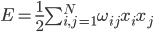
Where
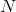
- the number of neurons used. In this case, each memorized image will correspond to a local energy minimum.
Although the Hopfield nets are very simple, they illustrate the three fundamental properties of the brain. The first is the existence of the brain in dynamics, when any external or internal perturbations force us to leave the state of the current local minimum of energy and go on to a dynamic search for a new one. The second is the ability to come to a quasistable state, determined by the previous memory. The third is the associativity of transitions, when a certain generalized proximity is constantly traced in a change of descriptive states.
Like the Hopfield network, our model is initially dynamic. It cannot exist in a static state. Any wave exists only in motion. The induced neuron activity triggers an identifier wave. These waves cause the activity of patterns that recognize familiar wave combinations. Patterns trigger new waves. And so without stopping.
But the dynamics of our networks are fundamentally different from the dynamics of Hopfield networks. In traditional networks, the dynamics are reduced to an iterative procedure for converting the state of the network to a steady state. In our case, the dynamics are similar to the processes that occur in algorithmic computers.
Wave propagation of information is a data transfer mechanism. The dynamics of this transmission is not the dynamics of iterative convergence, but the dynamics of the spatial propagation of an identification wave. Each cycle of propagation of the information wave changes the picture of the induced activity of neurons. The transition of the cortex to a new state means a change in the current description and, accordingly, a change in the picture of our thought. The dynamics of these changes, again, is not an iterative procedure, but forms a sequence of images of our perception and thinking.
Our wave model is much more complicated than a simple dynamic network. Later we will describe quite a few non-banal mechanisms regulating its work. Not surprisingly, the idea of associativity in our case turns out to be more complicated than associativity in Hopfield networks, and rather resembles the concepts inherent in computer models of data presentation.
In programming, associativity refers to the ability of a system to search for data that is similar to a sample. For example, if we access the database by specifying query criteria, then, in essence, we want to get all the elements that are similar to the pattern described by this query.
On a computer, you can solve the problem of associative search by simply iterating with checking all data for compliance with the search criteria. But a complete brute force is laborious, much faster the search is carried out if the data are prepared in advance so that they allow you to quickly form samples that meet certain criteria. For example, a search in the address book can be greatly accelerated by creating a table of contents by the first letter.
Properly prepared memory is called associative. The practical implementation of associativity can use index tables, hash addressing, binary trees, and similar tools.
Regardless of the implementation, associative search requires the specification of similarity or proximity criteria. As we have said, the main types of proximity are proximity by description, proximity by joint manifestation and proximity by a common phenomenon. The first speaks about the similarity in form, the rest about the similarity in some essence. It resembles a search for goods in the online store. If you enter a name, you will receive a list of products whose names will be close to the specified one. But besides this, you will most likely get another list, which will be called, something like: "those who are looking for this product often pay attention to ...". At the same time, the elements of the second list may by their descriptions in no way resemble the description formulated by the original request.
Let's see how the arguments about associativity apply to the concepts used in our model. Our concept is a set of patterns of neuron-detectors tuned to the same image. It seems that one pattern corresponds to a separate cortical minicolon. The image is a certain combination of signals on the receptive field of neurons. On the sensory zones of the cortex, the image can be formed by signals of topographic projection. At higher levels, an image is an activity pattern that arises around a neuron as waves of identifiers pass by it.
In order for a neuron to enter a state of evoked activity, it is required that the image accurately coincides with the pattern of weights on its synapses. So if a neuron is configured to detect a particular combination of concepts, then the wave identifier must contain a substantial part of the identifiers of each of them.
The triggering of a neuron, when most of the concepts that make up its characteristic stimulus are repeated, are called recognition. Recognition and related activity caused by it do not give generalized associativity. In this mode, the neuron does not respond to concepts that have a temporary proximity, nor to concepts, although they are included in the description of the characteristic stimulus for the neuron, but are found separately from the rest of the description.
The neurons that we use in our model, and which we compare with real brain neurons, are able to store information not only due to changes in synaptic weights, but also due to changes in metabotropic receptive clusters. Due to the latter, neurons are able to memorize fragments of pictures of environmental activity. The repetition of such a memorized picture does not lead to the appearance of the induced activity of a neuron consisting of a series of impulses, but causes a single spike. Whether or not a neuron will remember something in this way is determined by a number of factors, one of which is the change in the membrane potential of this neuron. An increase in the membrane potential causes a divergence of the split ends of the metabotropic receptors, which causes them to acquire the sensitivity that is necessary for memorizing.
When a neuron recognizes a characteristic image and enters a state of evoked activity, its membrane potential increases significantly, which allows it to memorize the surrounding activity patterns on the extra-synaptic part of the membrane.
It can be assumed that at the time of the evoked activity the neuron remembers all the wave patterns surrounding it. Such an operation has a very definite meaning. Suppose that we have a complete description of what is happening, consisting of a large number of concepts. Some of them will allow a neuron to learn the concept, the detector of which is its pattern (minicolumn). Recognition will provide this concept of participation in the general description. At the same time, the neurons responsible for the concept itself will be fixed, which other concepts were included in the full descriptive picture.
This fixation will occur on all neurons that make up our detection pattern (minicolumn). Regular repetition of such a procedure will lead to the accumulation on the surface of neuron detectors of receptive clusters that are sensitive to certain combinations of identifiers.
It can be assumed that the more often a concept will occur together with the activity of the detector pattern, the higher will be the likelihood that its independent appearance will be determined by extra-synaptic receptors and cause a single spike. That is, if there is a consistency between manifestations in the manifestation, then the neurons of the same concept will react with a single spike when another associatively associated concept appears in the wave description.
The simultaneous single spike of neurons of a single detection pattern is the basis for triggering the corresponding identification wave. It turns out that by setting one concept and extending its wave identifier, you can get in the wave description a set of concepts associated with it. This can be compared with how the database on request provides a list of all records that fall under the criteria of this query. After receiving the list from the database, we use additional algorithms to continue working with this list. Similarly, you can imagine the work of the brain. Getting access to associations is only one of the stages of its work. On the activity of neurons, you can impose additional restrictions that will allow only part of the associations to break into the wave description. The essence of these additional restrictions largely determines the informational procedures inherent in thinking.


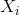 . Memorization takes place by adjusting the scales so that:
. Memorization takes place by adjusting the scales so that: 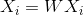
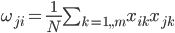
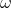 - a matrix made up of weights of neurons, and
- a matrix made up of weights of neurons, and 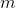 - the number of memorized images. Matrix diagonal
- the number of memorized images. Matrix diagonal 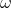 relies zero, which means the absence of the influence of neurons on themselves. The weights defined in this way determine the stable states of the network corresponding to the memorized vectors.
relies zero, which means the absence of the influence of neurons on themselves. The weights defined in this way determine the stable states of the network corresponding to the memorized vectors. 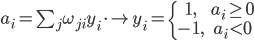
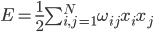
 - the number of neurons used. In this case, each memorized image will correspond to a local energy minimum.
- the number of neurons used. In this case, each memorized image will correspond to a local energy minimum.
Comments
To leave a comment
Logic of thinking
Terms: Logic of thinking