9.2. Indices

No matter how the indexes are organized in a specific DBMS, their main purpose is to ensure effective direct access to the relation tuple by key. Typically, an index is defined for a single relationship, and the key is the value of the attribute (possibly composite). If the index key is a possible relation key, then the index must have the uniqueness property, i.e. do not contain duplicate key. In practice, the situation usually looks the opposite: when declaring the primary key of a relationship, a unique index is automatically started, and the only way to declare a possible key other than the primary key is to explicitly create a unique index. This is due to the fact that in order to verify the preservation of the uniqueness property of a possible key, index support is somehow required.

Since many language-level operations require the relationship to be sorted according to the values ​​of some attributes, a useful property of the index is to ensure that the tuples of a relationship are consistently viewed in a range of key values ​​in ascending or descending order of key values.

Finally, one of the ways to optimize the performance of relationship equilibrium (the most common of the number of expensive operations) is the organization of so-called multi-indices for several relations that have common attributes. Any of these attributes (or a set of them) can act as a multi-index key. The key value is mapped to a set of tuples of all related multi-index relations, the values ​​of the selected attributes of which coincide with the key value.

The general idea of ​​any organization of an index that supports direct access by key and sequential browsing in ascending or descending order of key values ​​is storing an ordered list of key values ​​with a binding to each key value of a list of tuple identifiers. One organization of the index differs from the other mainly in the way of finding a key with a given value.

9.2.1. B-trees

Apparently, the most popular approach to organizing indexes in databases is to use the B-tree technique. From the point of view of an external logical representation, a B-tree is a balanced, highly branched tree in external memory. Balance means that the length of the path from the root of the tree to any leaf is the same. Tree branching is a property of each tree node to refer to but a large number of child nodes. From the point of view of physical organization, a B-tree is represented as a multi-list structure of external memory pages, i.e. each node of the tree corresponds to a block of external memory (page). Internal and leaf pages usually have a different structure.

In a typical case, the structure of the inner page is as follows:

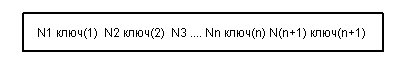
The following properties are maintained:

• key (1) <= key (2) <= ... <= key (n);
• in the tree page Nm there are keys k with values ​​key (m) <= k <= key (m + 1).

A leaf page usually has the following structure:

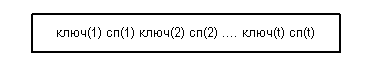
Sheet page has the following properties:

• key (1)
• Cn (r) - ordered list of identifiers of tuples (tid), including the value of the key (r);
• leaf pages are linked by a single or bidirectional list.

Search in a B-tree is the passage from the root to the leaf in accordance with the specified key value. Note that since trees are highly branched and balanced, to perform a search for any key value you will need the same (and usually small) number of exchanges with external memory. More precisely, in a balanced tree, where the lengths of all paths from root to leaf are the same, if n keys are placed in the inner page, then storing m records requires a tree of log _n (m) depth, where log _n calculates the logarithm of the base n . If n is large enough (the usual case), then the depth of the tree is small, and a quick search is performed.

The main "highlight" of B-trees is the automatic maintenance of the property of balance. Consider how this is done when performing entries and deletion of records.

When a new entry is made:

• Search leaf page. In fact, the usual search by key is performed. If the B-tree does not contain a key with the specified value, then the page number will be obtained in which it should be contained, and the corresponding coordinates inside the page.
• Putting the record into place. Naturally, all work is done in memory buffers. The sheet page to which the record is to be written is read into the buffer, and an insert operation is performed in it. The buffer size must be larger than the external memory page size.
• If after inserting a new record, the size of the used part of the buffer does not exceed the page size, then the write operation ends there. The buffer can be immediately pushed into external memory, or temporarily stored in RAM, depending on the buffer management policy.
• If a buffer overflow occurs (i.e., the size of its usable part exceeds the page size), the page is split. To do this, a new page of external memory is requested, the used part of the buffer is broken roughly speaking in half (so that the second half also starts with a key), and the second half is written to the newly allocated page, and the old page size is modified by the amount of free memory. Naturally, the links on the list of leaf pages are modified.
• To provide access from the root of the tree to the newly wound page, it is necessary to modify the inner page, which is the ancestor of the previously existing leaf page, i.e. insert into it the corresponding key value and a link to a new page. When performing this action, the inner page may now overflow again, and it will be split into two. As a result, you will need to insert the key value and a link to a new page into the inner ancestor page up the hierarchy, etc.
• The limiting case is the overflow of the root page of the B-tree. In this case, it also splits into two, and a new root page of the tree is started, i.e. its depth is increased by one.

When deleting a record, the following actions are performed:

• Search records by key. If the record is not found, it means you do not need to delete anything.
• The real deletion of an entry in the buffer in which the corresponding leaf page is read.
• If, after performing this sub-operation, the size of the area occupied by the buffer is such that its sum with the size of the area occupied in leaf pages that are the left or right brother of this page is larger than the page size, the operation is completed.
• Otherwise, it is merged with the right or left brother, i.e. A new image of the page containing general information from this page and its left or right brother is produced in the buffer. The leaf page that has become unnecessary is entered into the list of free pages. The list of leaf pages is adjusted accordingly.
• To eliminate the possibility of access from the root to the liberated page, it is necessary to remove the corresponding key value and the link to the liberated page from the internal page - its ancestor. There may be a need to merge this page with its left or right brothers, etc.
• The limiting case is the complete emptying of the root page of the tree, which is possible after the merging of the last two descendants of the root. In this case, the root page is freed, and the tree depth is reduced by one.

As you can see, when performing insertion and deletion operations, the B-tree balance property is preserved, and the external memory is consumed quite economically.

The problem is that splitting and merging may occur too often when performing modification operations. To achieve efficient use of external memory while minimizing the number of splits and merges, more sophisticated techniques are used, including:

• anticipatory splitting, i.e. page splitting not when it is full, but somewhat earlier, when the degree of filling of the page reaches a certain level;
• transfusions, i.e. maintaining an equilibrium filling of adjacent pages;
• 3-in-2 fusions, i.e. spawning two leaf pages based on the contents of three adjacent ones.

It should be noted that the organization of multi-access to B-trees, which is typical when used in a DBMS, has to solve a number of non-trivial problems. Of course, coarse solutions are obvious, for example, the exclusive capture of a B-tree for the entire execution of a modification operation. But there are more subtle solutions, consideration of which is beyond the scope of our course.

And one final note on B-trees. In the literature, it is common to refer to the type of trees examined by us as B * or B + trees.

9.2.2. Hashing

An alternative and increasingly popular approach to index organization is the use of hashing techniques. This is a very broad topic that deserves separate consideration. We confine ourselves to a few remarks. A common idea of ​​hashing methods is to apply a convolution function (hash function) to a key value that produces a smaller value. The key value convolution is then used to access the entry.

In the simplest, classic case, the key convolution is used as an address in a table containing keys and records. The main requirement for the hash function is the uniform distribution of the value of convolution. In the event of collisions (the same convolution for several key values) overflow chains are formed. The main limitation of this method is the fixed size of the table. If the table is too full or overflowed, but there are too many overflow chains, and the main advantage of hashing - access to the record is almost always in one access to the table - will be lost. Expansion of the table requires its complete rework based on the new hash function (with a larger convolution value).

In the case of databases, such actions are completely unacceptable. Therefore, it is usual to introduce intermediate reference tables containing the key values ​​and addresses of entries, and the entries themselves are stored separately. Then, when the directory overflows, only its reworking is required, which causes less overhead.

To avoid the need for complete rework of reference books, they often use B-tree technique with splits and merges when organizing them. The hash function changes dynamically depending on the depth of the B-tree. By means of additional technical tweaks, it is possible to achieve the preservation of the order of records in accordance with the key values. In general, B-tree and hashing methods are increasingly converging.