Lecture
The optimizing transformations that we considered above left the internal representation of the query nonprocedural.
A procedural view or a plan for the execution of a request is called its view, which details the procedure for performing access operations to the physical layer database. As a rule, in relational DBMS, a data management subsystem at the physical level is allocated. In System R, such a subsystem is called RSS (Relational Storage System) and provides a simple interface that allows you to consistently view relationship tuples that satisfy specified conditions on field values using indexes or simply scanning database pages. In addition, RSS allows you to produce sorted temporary files and add, delete and modify individual tuples. Similar subsystems are explicitly or implicitly distinguished in all similar DBMSs.
Naturally, prior to the execution of a request, it is necessary to work out its procedural representation. Since, generally speaking, it is chosen ambiguously, it is necessary to choose one among alternative query plans in accordance with certain criteria. As a rule, the criterion for choosing a query execution plan is to minimize the cost of execution.
Thus, when processing the request at the stage following the logical optimization, two problems are solved. The first task: based on the internal presentation of the query and information characterizing the database control structures (for example, indexes), select a set of potentially possible execution plans for this query. The second task: to estimate the cost of fulfilling a request in accordance with each alternative plan and select the plan with the lowest cost.
In the traditional approach to the organization of optimizers, both problems are solved on the basis of fixed algorithms built into the optimizer. The optimizer can be calculated on the fact that the restriction of any relationship in accordance with a given predicate can be performed by some consistent viewing of the relationship. So request
SELECT EMPNAME FROM EMP WHERE
DEPT # = 6 AND SALARY> 15.000 can be performed by successively scanning the EMP relationship with a choice of tuples with DEPT # = 6 and SALARY> 15.000; scanning the relationship through the index I1, defined on the DEPT # field, with the condition of access to the index DEPT # = 6 and the sample condition of the SALARY tuple> 15.000; finally, scanning the relationship through the I2 index defined on the SALARY field, with the condition for accessing the SALARY index> 15.000 and the sampling condition of the DEPT tuple # = 6.
Similarly, strategies for performing more complex operations — relational connection of relations, computing aggregate functions on groups of relation tuples, etc. — are also fixed. For example, in System R, for (equi) joining two relationships, two basic strategies are used: the nested loop method and the merge sort method.
The optimizer component that generates the executed query plans has a rather complex organization; Generation of a complex query execution plan is a multi-step process in which the properties of temporary database objects created during the execution of a query on a given plan are taken into account. For example, let the query be defined over three relations and have two join predicates:
SELECT R1.C1, R2.C2, R3.C3 FROM R1, R2, R3 WHERE R1.C4 = R2.C5 AND R2.C5 = R3.C6.
Then, if in the query plan, the order of making connections is first selected from R1 to R2, and then the obtained time relation to R3, and the merge sorting method is selected to make the first connection, then the time relation will be obviously sorted by C5, and one sort is not required if the second connection will be performed by the same method.
The optimizer component, which is responsible for generating multiple alternative plans for executing a query, is based on the decomposition strategies of the query into elementary components and the strategies for performing the elementary components. The first group of strategies determines the search space for the optimal execution plan for the query, the second is aimed at ensuring that the effective execution plans for the query are in this space. The key to ensuring the effective execution of a complex query is to have effective strategies for performing elementary components. This is a very important question, but here we don’t touch it: the query optimizer uses the specified strategies. Consider a problem that is more relevant to the optimizer - a reasonable choice of a plan for executing a query from a variety of alternative plans.
After generating a set of plans for executing a query based on reasonable decomposition strategies and effective strategies for performing elementary operations, you need to select one plan, according to which the actual execution of the query will occur. If the wrong choice, the request will be executed inefficiently. First of all, it is necessary to determine what is meant by the efficiency of the query. This concept is ambiguous and depends on the specifics of the DBMS operating environment. In some conditions, it can be assumed that the effectiveness of the execution of a request is determined by the time of its execution, i.e. reactivity of the system with respect to the requests it processes. In other conditions, the overall throughput of the system with respect to a mixture of concurrently executed queries is decisive. Then a measure of the effectiveness of a request can be considered the amount of system resources required for its execution, etc.
Following the accepted terminology, we will talk about the cost of the query execution plan, determined by the processor resources and external memory devices that are consumed when the query is executed.
In traditional relational DBMS, the subsystem of access control to data on external memory (RSS in System R) is allocated. Data on external memory is traditionally stored in a locked form; A database occupies a set of blocks of one or more disk volumes. It is assumed that the means of access to the blocks of external memory generate incomparably less overhead.
As a rule, the data access control subsystem on external memory buffers the database blocks in RAM. Each database block read into RAM for query execution is stored in one of the buffers in the buffer pool of the DBMS until it is preempted out of it by another database block. This feature of the DBMS is essential for increasing the overall efficiency of the system, but is not taken into account (with the exception of a particular but important case) when estimating the values of the plans for the execution of a query. In any case, the query cost component associated with the resources of external memory devices monotonously depends on the number of external memory blocks that will be required to access the request.
On the other hand, the number of external memory blocks that are required to access when executing a query monotonously depends on the number of tuples affected by the query.
This implies the importance of the predicate restriction indicator, which characterizes the proportion of tuples in a relation that satisfy a given predicate, and is called the predicate selectivity degree. The degree of selectivity of simple predicates of the form RC op const, where RC defines the name of a database relation field, op is a comparison operation (=,! =,>, <,> =, <=), And const is a constant, are the basis for estimating the cost of plans request. The accuracy of the estimates of the degrees of selectivity determines the accuracy of the overall estimates and the correctness of the choice of the optimal query plan.
The degree of selectivity of the predicate RC op const depends on the type of comparison operation, the value of the constant and the distribution of the values of the field C of the relation R in the database. The first two selectivity parameters may be known when conducting assessments, but the true distributions of the values of the relationship fields are usually unknown. There are a number of approaches to approximate definitions of distributions based on statistical information. Next we look at the most interesting of them.
If the degree of selectivity of the predicate of the constraint of a relation is known, then the power of the resulting relation is known (usually, the powers of the stored relations are known when processing the request). But the evaluation formulas take into account the number of exchanges with external memory required to complete the request. Of course, the number of tuples is the upper estimate of the required number of exchanges, but this estimate can be very high. It all depends on the distribution of tuples in blocks of external memory. In some cases, you can get a more accurate estimate of the number of blocks.
Finally, for complex queries, including, for example, joining more than two relations, it is required to estimate the sizes of intermediate relations arising in the process of executing a query. In order to estimate the power of the result of combining two relations, generally speaking, it is necessary to know the degree of selectivity of the compound predicate with respect to the direct product of operand relations. In general, the degree of selectivity of such a predicate cannot be determined on the basis of simple statistical information. Rough heuristic estimates are usually used, although approaches are also proposed that provide greater accuracy.
The System R approach is based on two basic assumptions about the distribution of values of relationship fields: it is assumed that the field values of all database relations are evenly distributed and that the values of any two fields are independently distributed. The first assumption allows us to estimate the selectivity of simple predicates on the basis of poor statistical information about the database. Estimates of the number of blocks in which a known number of tuples reside are based on the second assumption. These two assumptions are criticized by System R. They are made solely in order to simplify the optimizer and cannot be theoretically justified. You can give examples of databases for which these assumptions are not justified. In these cases, the System R optimizer estimates will be incorrect.
The database directories for each relation R store the number of tuples in a given relation (T) and the number of external memory blocks in which the tuples of the relationship (N) are located; For each C field of a relation, the number of different values of this field (CD), the minimum stored value of this field (CMin) and the maximum value (CMax) are stored.
Given such information, taking into account the first basic assumption, the degree of selectivity of simple predicates is calculated simply (and exactly, if the distribution is in fact uniform). Let SEL (P) be the degree of selectivity of the predicate P.
Then
SEL (RC = const) = CD / (CMax - CMin)
(with a uniform distribution, the degree of selectivity of such a predicate does not depend on the value of the constant).
SEL (RC> const) = (CMax - const) / (CMax - CMin)
etc.
When estimating the number of blocks in which tuples that satisfy the RC op const predicate are located, cases of clustering or nonclustering relationships across field C are distinguished. These estimates make sense only when considering the option of scanning a relationship using an index on a field C. When viewing a relationship without using an index you will need to always refer to exactly N blocks of external memory.
Assumptions about the uniformity of the distribution of the values of the attributes of relations make it possible to fairly simply evaluate the cardinalities of the relations, which are the results of two-place relational and set-theoretic operations on relations.
Predicate selectivity estimates are also used to estimate CPU resource costs. It is assumed that the main part of the processor processing is done in RSS. Therefore, processor costs are measured by the number of calls to RSS, which corresponds to the number of tuples obtained by scanning a stored or temporary relationship, i.e. the selectivity of a logical expression consisting of simple predicates (the condition of sampling the level of RSS). Assumptions about the uniformity and independence of the values of different relation fields make it easy to estimate the selectivity of a logical expression composed of simple predicates, with their known degrees of selectivity.
In fact, in System R, the predicate selectivity is not evaluated in its pure form. The optimizer estimates are based on a fixed set of elementary evaluation formulas based on statistical information about the database. Each formula corresponds to some elementary action of the system; The execution of any request consists of a combination of some elementary actions. Examples of elementary actions are limiting a relationship by scanning it through a clustered index, sorting the relationship, combining two previously sorted relations, etc. The overall assessment of the query execution plan is performed in an iterative process, starting with estimates of elementary operations on stored relationships.
Let us turn to the consideration of approaches to more accurate estimates of the cost of executing the query plans. These approaches can be divided into two classes. When using first-class approaches, the optimizer maintains a rigid structure similar to that of the System R optimizer, but the estimation is based on more accurate statistical information characterizing the distribution of values. The second-class sentences are more revolutionary, and they are based on the fact that in order to produce plans for fulfilling queries and evaluating them, the optimizer must be supplied with some information specific to a particular area of applications.
If you reject the assumption that the values of the field of a relation are evenly distributed, you must be able to establish the real distribution of values. There are two basic approaches to estimating the distribution of values of a relation field: parametric and based on the method of signatures. The System R approach is a trivial particular case of the parametric distribution estimation method - any distribution is estimated as uniform. In a more developed approach, it was proposed to use a series of Pearson distributions, which include the distributions from uniform to normal, to estimate the real distribution of the ratio field values. The distribution is selected from a series by calculating several parameters based on samples of actual values encountered. Examples of the practical application of this approach are unknown to us.
The method of estimating distribution based on signatures as a whole can be described as follows. The field of values of the field is divided into several intervals. For each interval, the number of field values falling into this interval is determined in some way. Within the interval, values are considered to be distributed according to some fixed law (as a rule, a uniform approximation is taken). Let us consider two alternative approaches related to the signature description of distributions.
In the traditional approach, the field range of the field is divided into N intervals of equal size, and for each interval, the number of field values from the tuples of a given relation falling into the interval is calculated. Suppose that EMP is extended by another AGE field - employee age. Let all in organization 60 employees work in age from 10 to 60 years. Then the histogram depicting the distribution of the AGE field values can have the form shown below. The histogram is based on the division of the range of values of the AGE field into 10 intervals.
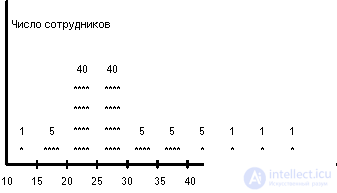
Let us consider how the selectivity of simple predicates given on the AGE field can be estimated using such a histogram. Let the range of values of AGE S i be K i values. Then SEL (EMP.AGE = const), if the value of the constant falls within the range of values of S i , can be estimated as follows: 0 <= SEL (EMP.AGE) <= K i / T (T is the total number of tuples with respect to EMP) . Hence, the average estimate of the degree of selectivity of the predicate is K i / (2 (T). For example, SEL (AGE = 29) is estimated at 40/200 = 0.2, and SEL (AGE = 16) is estimated at 5/200 = 0.025. This, of course , significantly more accurate estimates than those that can be obtained from assumptions about the uniformity of distributions, but not so well with the estimates of the selectivity of simple predicates with inequalities.
For example, suppose you want to evaluate the degree of selectivity of the predicate EMP.AGE <const. If the value of the constant falls within the interval S i , and SUMi is the total number of AGE values falling into the intervals S 1 , S 2 , ..., S i , then SUM i-1 / T <= SEL (AGE <const) <= SUM i / T. Then the average estimate of the degree of selectivity (SUM i-1 + SUM i ) / (2 (T), and the estimate error can reach half the weight of the subregion that the predicate constant falls into. The most annoying thing is that the estimate error depends on the values of the constant and the more, the more field values are contained in the corresponding histogram interval, for example, SEL (AGE <29) is estimated as 46/100 <= SEL (AGE <29) <= 86/100, from which the estimates degree of selectivity (46 + 86) / 200 = 0.66, while the estimation error can reach 0.2 V at the same time SEL (AGE <49) can be estimated much more accurately..
To eliminate this defect, another approach was proposed to the description of the distribution of the values of the ratio field. Идея подхода состоит в том, что множество значений поля разбивается на интервалы вообще говоря разного размера, чтобы в каждый интервал (кроме, вообще говоря, последнего) попадало одинаковое число значений поля. Количество интервалов выбирается исходя из ограничений по памяти, и чем оно больше, тем точнее получаемые оценки. При разбиении области значений на десять интервалов получаемая псевдогистограммная картина распределений значений поля AGE показана на рисунке ниже.
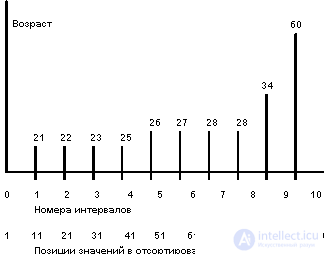
The range of values of the AGE field of the EMP relationship is divided into 10 intervals in such a way that exactly 10 values of the AGE field fall into each interval. Intervals have different sizes. The boundary values of the intervals are shown above the vertical lines. In a pseudohistogram, the intervals are allowed, the right and left borders of which coincide, for example, the interval (28.28). It was formed due to the presence in relation to the EMP of a large (more than ten) number of tuples with the value AGE = 28.
When using the "pseudohistogram" errors in the estimates of the degrees of selectivity of predicates with an operation other than equality, are reduced. The size of the error does not depend on the value of the constant and decreases with increasing number of intervals.
Недостатком метода псевдогистограмм по сравнению с методом гистограмм является необходимость сортировки отношения по значениям поля для построения псевдогистограммы распределений значений этого поля. Известен подход, позволяющий получить достоверную псевдогистограмму без необходимости сортировки всего отношения.
Подход основывается на статистике Колмогорова, из которой применительно к случаю реляционных баз данных следует, что если из отношения выбирается образец из 1064 кортежей, и b - доля кортежей в образце со значениями поля C < V, то с достоверностью 99% доля кортежей во всем отношении со значениями поля C < V находится в интервале [b-0.05, b+0.05]. При уменьшении мощности образца достоверность, естественно, уменьшается.
Comments
To leave a comment
Databases IBM System R - relational DBMS
Terms: Databases IBM System R - relational DBMS