Lecture
Let us now dwell on some important properties of relations that follow from the above definitions:
The property that relations do not contain duplicate tuples follows from the definition of a relation as a set of tuples. In the classical theory of sets, by definition, each set consists of different elements.
This property implies that each relation has a so-called primary key — a set of attributes whose values uniquely determine the tuple of the relation. For each relationship, at least its full set of attributes has this property. However, the formal definition of a primary key requires ensuring its “minimality”, i.e. the set of attributes of the primary key should not include such attributes that can be dropped without affecting the main property - uniquely identify the tuple. The concept of a primary key is extremely important in connection with the concept of database integrity.
Looking ahead, we note that in many practical implementations of RDBMS, a violation of the uniqueness property of tuples for intermediate relations generated implicitly when executing queries is allowed. Such relationships are not sets, but multisets, which in some cases allows to achieve certain advantages, but sometimes leads to serious problems.
The property of the lack of ordering of tuples of a relation is also a consequence of the definition of an instance relation as a set of tuples. The absence of the requirement to maintain order on the set of relations tuples gives additional flexibility to the DBMS when storing databases in external memory and when performing queries to the database. This does not contradict the fact that when formulating a query to a database, for example, in SQL, you can require sorting the resulting table according to the values of some columns. Such a result, generally speaking, is not a relation, but some ordered list of tuples.
Relationship attributes are not ordered, because by definition, the relationship scheme is a set of pairs {attribute name, domain name}. The attribute name is always used to reference an attribute value in a relation tuple. This property theoretically allows, for example, to modify the schemas of existing relations not only by adding new attributes, but also by deleting existing attributes. However, in most existing systems such a possibility is not allowed, and although the orderliness of the set of relationship attributes is not explicitly required, often their order is used as an implicit order of attributes in the linear form of the definition of the relationship scheme.
The values of all attributes are atomic. This follows from the definition of a domain as a potential set of values of a simple data type, i.e. among the values of the domain can not contain sets of values (relations). It is customary to say that in relational databases only normalized relations or relations presented in the first normal form are allowed. A potential example of a non-normalized relationship is the following:
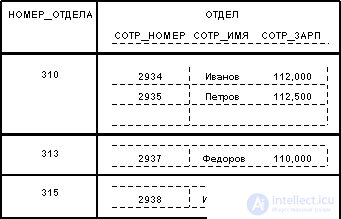
It can be said that here we have a binary relation, the values of the attribute DEPARTMENTS are relations. Note that the original relationship EMPLOYEES is the normalized version of the relationship DEPARTMENTS:
| SOTR_NOMER | CLEAR_NAME | SOTR_ZARP | SOTR_OTD_NOMER | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2934 | Ivanov | 112,000 | 310 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2935 | Petrov | 144,000 | 310 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2936 | Sidorov | 92,000 | 313 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2937 | Fedorov | 110,000 | 310 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2938 | Ivanova | 112,000 | 315 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Normalized relationships form the basis of the classical relational approach to database organization. They have some limitations (it is not convenient to present any information in the form of flat tables), but they greatly simplify the manipulation of data. For example, consider two identical tuple insertion operators:
Enroll employee Kuznetsov (pass number 3000, salary 115,000) to department number 320 and
Enroll the employee Kuznetsov (pass number 3000, salary 115,000) in department number 310.
If information about employees is presented in the form of a relation EMPLOYEES, both operators will be executed in the same way (insert a tuple in relation to EMPLOYEES). If we work with a non-normalized relation DEPARTMENT, then the first operator will result in the insertion of a tuple, and the second - in adding information about Kuznetsov to the plural value of the DEPARTMENT attribute of the primary key tuple 310.
Comments
To leave a comment
Databases IBM System R - relational DBMS
Terms: Databases IBM System R - relational DBMS