4.3. Relational data model

When in the previous sections we talked about the basic concepts of relational databases, we did not rely on any specific implementation. These considerations apply equally to any system that was built using the relational approach.

In other words, we used the concept of the so-called relational data model. A data model describes a set of generic concepts and features that all specific DBMSs and databases they manage, if they are based on this model, must possess. Having a data model allows you to compare specific implementations using one common language.

Although the concept of a data model is general, and we can talk about hierarchical, network, some semantic, etc. data models, it should be noted that this concept was introduced in relation to relational systems and is most effectively used in this context. Attempts to rectilinearly apply similar models to dormant organizations show that the relational model is too “big” for them, and for post-relational organizations it turns out to be “small”.

4.3.1. general characteristics

The most common interpretation of the relational data model seems to be that of Data, which reproduces it (with various refinements) in almost all of its books. According to Data, the relational model consists of three parts, describing different aspects of the relational approach: the structural part, the manipulation part, and the integral part.

In the structural part of the model, it is fixed that the only data structure used in relational databases is the normalized n-ary ratio. In fact, in the previous two sections of this lecture, we looked at precisely the concepts and properties of the structural component of the relational model.

In the manipulative part of the model, two fundamental mechanisms for manipulating relational databases are established: relational algebra and relational calculus. The first mechanism is based mainly on the classical set theory (with some clarifications), and the second is based on the classical logical apparatus of the first-order predicate calculus. We will consider these mechanisms in more detail in the next lecture, but for now let us just note that the main function of the manipulative part of the relational model is to provide a measure of the relationality of any particular language of relational databases: a language is called relational if it has no less expressiveness and power than relational algebra or relational calculus.

4.3.2. Entity and link integrity

Finally, in the integral part of the relational data model, two basic integrity requirements are fixed, which must be supported in any relational DBMS. The first requirement is called the entity integrity requirement . The object or entity of the real world in relational databases corresponds to tuples of relationships. Specifically, the requirement is that any tuple of any relation is distinguishable from any other tuple of this relation, i.e. in other words, any relationship must have a primary key. As we saw in the previous section, this requirement is automatically satisfied if the system does not violate the basic properties of relations.

The second requirement is called reference integrity and is somewhat more complex. Obviously, while respecting the normalization of relations, complex entities of the real world are represented in a relational database as several tuples of several relations. For example, imagine that we need to present in the relational database the entity DEPARTMENT with the attributes OTD_NOMER (department number), OTD_COL (number of employees) and OTD_SEDR (set of department employees). For each employee you need to store SOTR_NOMER (employee number), SOTR_NAME (employee's name) and SOTR_ZARP (employee salary). As we shall soon see, with proper design the appropriate database it will be two relationship: DEPARTMENTS (OTD_NOMER, OTD_KOL) (primary key - OTD_NOMER) and employees (SOTR_NOMER, SOTR_IMYA, SOTR_ZARP, SOTR_OTD_NOM) (primary key - SOTR_NOMER).

As you can see, the attribute SOTR_OTD_NOM appears in relation to EMPLOYEES not because the department number is an employee's own property, but only in order to be able to restore the full essence DEPARTMENT if necessary. The value of the attribute COTR_OTD_NOM in any tuple of the relationship EMPLOYEES must match the value of the attribute OED_NOM in some tuple of the relation DEPARTMENTS. An attribute of this kind is called a foreign key , since its values ​​uniquely characterize entities represented by tuples of some other relation (that is, they specify the values ​​of their primary key). It is said that the relation in which the foreign key is defined refers to the corresponding relation in which the same attribute is the primary key.

Reference integrity requirement, or a foreign key requirement, is that for each foreign key value appearing in the referencing relationship, there must be a tuple with the same primary key value in the referenced relation, or the foreign key value must be undefined (i.e. not to indicate anything). For our example, this means that if an employee has a department number, then this department must exist.

Entity integrity and reference constraints must be maintained by the DBMS. To maintain the integrity of an entity, it is sufficient to guarantee that in any relation there are no tuples with the same primary key value. The integrity of the links is somewhat more complicated.

It is clear that when updating a referencing relationship (inserting new tuples or modifying a foreign key value in existing tuples), it is enough to ensure that incorrect foreign key values ​​do not appear. But what about when you remove a tuple from the relationship to which the link leads?

Here there are three approaches, each of which maintains link integrity. The first approach is that it is prohibited to delete the tuple to which the references exist (that is, you must first either delete the referencing tuples or change the values ​​of their foreign key accordingly). In the second approach, when deleting a referenced tuple, the value of the foreign key automatically becomes undefined in all referencing tuples. Finally, the third approach (cascade deletion) is that when you delete a tuple from a referenced relationship, all referring tuples are automatically deleted from the referencing relationship.

In developed relational DBMSs, you can usually choose a way to maintain the integrity of the links for each individual situation of determining a foreign key. Of course, to make such a decision, it is necessary to analyze the requirements of a specific application area.

3.1. Basic concepts of the relational model

The concept of a relational data model was proposed in 1969 by Edgar Codd, a well-known database expert, and in 1970 he published it. A relational model is a collection of data consisting of a set of two-dimensional tables . In set theory, the table corresponds to the term relation, the physical representation of which is the table, hence the name of the model — relational. The relational model is a convenient and most familiar form of data presentation.

When tabular data organization there is no hierarchy of elements. Rows and columns can be viewed in any order, so there is high flexibility in selecting any subset of elements in rows and columns.

Any table in a relational database consists of rows, which are called records , and columns, which are called fields . At the intersection of the rows and columns are specific data values. For each field, a set of its values ​​is defined, for example, the Month field can have twelve values.

The structure of the table in the relational database is characterized as follows:

• · It consists of a collection of columns;
• · Each column has a unique, that is, not repeating in other columns, name;
• · The sequence of columns in the table is not significant;
• · All rows of the table are organized according to the same structure, that is, they have the same number of details and have the same length;
• · There are no identical rows in the table;
• · The number of rows in the table is practically unlimited;
• · The sequence of rows in the table is not significant;
• · When performing manipulations with a table, all rows and columns can be viewed in arbitrary order regardless of their content and meaning.

For this type of model there is a developed mathematical apparatus — relational algebra. In relational algebra, the named relation column is called an attribute, and the set of all possible values ​​of a particular attribute is called a domain . Table rows with values ​​of different attributes are called tuples . For example, in the table shown in fig. 7, tuples are d _{i 1,} d _{i 2} , ..., d _in (i = 1,2, ... m); and the domains are d _1k, d _2k , ..., d _mk (k = 1,2, ... n). The number of attributes contained in a relation determines its degree , and the number of tuples determines the cardinality of the relation .

Fig. 7. Domains and Relations Tuples

One or more attributes whose values ​​uniquely identify the tuple of a relationship is called its key , or primary key, or key field. That is, a key field is a field whose values ​​are not repeated in this table. So, if the table contains a list of employees, and there are fields in it: Personnel number, full name, Position, then the Personnel number field can be taken as a key. The basic concepts of the relational model are illustrated in Fig. eight.

Fig. 8. Basic concepts of the relational data model

The records in the table are stored ordered by key. The key can be simple, consisting of one field, and difficult, consisting of several fields. A complex key is selected in cases where no field of the table uniquely identifies a record.

In addition to the primary key, the table may include secondary keys, also called foreign keys, or indexes. An index is a field or a collection of fields whose values ​​exist in several tables and which is the primary key in one of them. Index values ​​can be repeated in a table. The index provides a logical sequence of records in the table, as well as direct access to the record.

For the primary key, only one row is always searched, and for the secondary key - a group of rows with the same primary key values ​​can be searched. Keys are needed to uniquely identify and streamline table entries, and indexes to streamline and speed up searches.

Indexes can be created and deleted, leaving the contents of the relational table entries unchanged. The number of indices, the names of the indices, the correspondence of the indices to the fields of the table is determined when creating the table schema.

Indexes allow you to efficiently implement data search and processing, create additional index files. When adjusting data, indexes are automatically ordered, the location of each index is changed according to the accepted condition (ascending or descending values). The records of the relational table themselves are not moved when new records are deleted or included, and the values ​​of their key fields change.

Using indexes and keys , links are established between the tables. A relationship is established by assigning the foreign key values ​​of one table to the primary key values ​​of another. A group of related tables is called a data schema (Fig. 9) . Information about tables, their fields, keys, etc. called metadata.

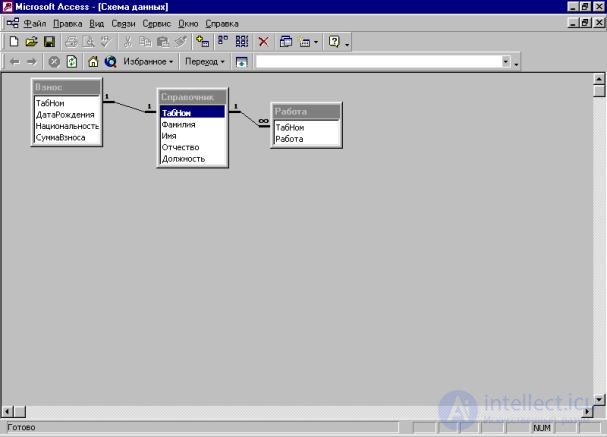
Fig. 9 Data Scheme in Access Database

The primary key of any table must contain unique (non-duplicate) non-empty values ​​for this table. The database management system should control the uniqueness of the primary keys. If you try to assign a value to a primary key that already exists in another entry in the table, the primary key error message is displayed.

With the advent of PC, relational systems began to dominate among database systems. Three factors contributed to the rapid spread of relational models.

First, in the relational system, data is presented in the form of tables (relationships) found in everyday practice. Search and data processing in these tables does not depend on their organization and storage in the machine’s memory.

Secondly, from a mathematical point of view, the relational base is a finite set of relations. Thus, the theory of relational databases becomes a field of mathematical logic and relational algebra.

Thirdly, the set of objects of the relational data model is homogeneous - the data structure is defined only in terms of relationships. The basic processing unit in the operations of the relational data model is not a record (as in network and hierarchical data models), but a set of records, that is, a relation.

In non-relational databases, it is difficult to transfer all the existing dependencies, that is, to associate data from different tables with each other. The relational database performs all these actions quite simply. Thanks to existing connections in relational databases, it is possible to avoid duplication of information, which facilitates the work and allows to avoid mistakes. In relational databases, it is also easy to avoid the establishment of erroneous relationships between different data tables.

Relational databases are easy to make changes. For example, if you change the address of a specific customer in the customer table, the corresponding information will automatically go to other tables related to the customer table.

Thus, the advantages of relational databases can be formulated as follows.

• · Simplified diagram of data presentation - in the form of a table.
• · Simplicity of tools support the relational model.
• · Optimization of access to the database, since the systems themselves choose the most effective sequence of actions.
• · Improving integrity and security , because the relational model can improve the expression of integrity requirements by using a high-level language.
• · Possibilities of various applications, including those designed for non-specialists in the field of programming .
• · Providing the user with high-level languages when working with a database.
• · Providing a methodological approach , since the main objective of the database model is the ability to describe the real world, which is the easiest to implement in the relational model.

The lack of a relational model is in the rigidity of the data structure, for example, it is impossible to specify a row of a table of arbitrary length, as well as the complexity of describing hierarchical and network connections.

Currently, many well-known database management systems use exactly the relational model of data representation -: these are dBase, FoxBase, FoxPro, Paradox, Oracle, Microsoft Access, Clarion, Clipper, Ingres; Domestic: PALMA, HyTech, etc.

3.2. Data Links

Data on objects in the database are related. These relationships are usually depicted as follows:

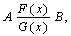
where a and b are objects;

F (x) is the type of connection between object A and object B;

G (x) is the type of connection between object B and object A.

The functions F (x) and G (x) can take the values ​​U - a single and N - a multiple bond. Usually consider four kinds of relationships.

One to one relationship (1: 1):

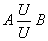
means that only one element of object B can correspond to each element of object A and vice versa, for example:

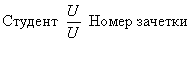
One-to-many relationship (1: N):

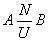
means that there may be instances of object A, which corresponds to more than one instance of object B. But at the same time only one instance of object A can correspond to each instance of object B, for example:

University 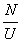Faculties; Group 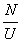Students

Connection many to one (N: 1)

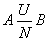
means that only one instance of object B can correspond to each instance of object A, but among the instances of object B there can be ones that correspond to several instances of object A, for example:

University 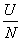Faculties; Buyers 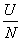Seller.

Obviously, if 1: N is the type of connection between A and B, then N: 1 is the type of connection between B and A.

Many to many connection (N: M), or group: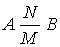

means that an instance of object A may exist, to which several instances of object B correspond and vice versa. For example:

Teachers 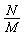Items; Buyers 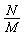Sellers.

3.3. Operations in relational databases

Each database has its own set of operations. These operations transfer databases from one state to another. Each operation includes the selection of data (selection) and the actions that will be performed on the selected data. The theoretical basis of a relational database is relational algebra, based on set theory and considering special operations on relations, and relational calculus , based on mathematical logic. For the manipulation of relational database data, the operations of the theory of relations are used. The main operations in the relational database are database update operations and relationship processing operations.

To database update operations относятся те операции, которые выполняют вставку новых кортежей, удаление ненужных, корректировку значений атрибутов существующих кортежей, а именно: это операции Включить , Удалить, Обновить.

Операция Включить требует задания имени отношения и предварительного формирования значений атрибутов нового кортежа. Обязательно должен быть задан ключ кортежа.

Операция Удалить требует наименования отношения, а также идентификации кортежа или группы кортежей, подлежащих удалению.

Операция Обновить выполняется для названного отношения и может корректировать как один, так и несколько кортежей. Например, если руководство фирмы приняло решение увеличить на одинаковую сумму все оклады сотрудников, то одной операцией Обновить будет откорректировано сразу несколько кортежей.

Что касается операций обработки, то они позаимствованы из реляционной алгебры. Существует несколько подходов к определению реляционной алгебры. Они отличаются набором операций и их интерпретацией. Рассмотрим набор операций, который предложил Э. Кодд. Согласно его подходу реляционная алгебра включает восемь операций, пять из которых являются базовыми: Выборка , Проекция, Умножение, Объединение, Вычитание.

Операция Выборка позволяет выбрать из отношения только те кортежи, которые удовлетворяют заданному условию.

При Проекции отношения на заданный набор его атрибутов получается новое отношение, создаваемое посредством извлечения из исходного отношения кортежей, содержащих указанные атрибуты.

При Умножении (декартовом произведении) двух отношений получается новое отношение, кортежи которого являются сцеплением (конкатенацией) кортежей первого и второго отношений.

В результате Объединения двух отношений получается третье, включающее кортежи, входящие хотя бы в одно отношение, то есть содержащее все элементы исходных отношений.

При Вычитании выдаются лишь те кортежи первого отношения, которые остались от вычитания второго отношения, то есть из первого отношения выбрасываются все кортежи второго.

Остальные три операции являются производными, они могут быть получены из основных операций, их называют дополнительными: Соединение, Пересечение , Деление.

Операция Соединение применяется к двум отношениям, имеющим общий атрибут. Результат этой операции для двух отношений по некоторому условию есть отношение, состоящее из кортежей, которые являются сочетанием первого и второго отношений, удовлетворяющих указанному условию. Результатом операции

Пересечение двух отношений является отношение, включающее все кортежи, входящие в оба отношения.

Операция Деления предполагает, что имеется два отношения: одно – бинарное (содержащее два атрибута), другое – унарное (содержащее один атрибут). В результате получается отношение, состоящее из кортежей, включающих значения первого атрибута кортежей первого отношения, но только таких, для которых множество значений второго атрибута первого отношения совпадает с множеством значений атрибутов второго отношения.

Отличительная особенность операций обработки отношений заключается в том, что единицей обработки в них являются не кортежи, а отношения: на входе каждой операции используется одно или два отношения, а результат выполнения операций – новое отношение. Смысл любой обработки реляционной базы данных состоит либо в обновлении существующих отношений, либо в создании новых, и результат всякого запроса к базе данных есть построение нового отношения, удовлетворяющего условиям выборки.

Рассмотрим некоторые, наиболее часто используемые операции реляционной алгебры, подробнее.

Операция Объединение ( C ₁ = A И B ) предполагает, что на входе задано два совместимых отношения, одинаковой размерности: А и В. Результат объединения есть отношение С ₁ , той же структуры, содержащее все кортежи отношения А и все кортежи отношения В (рис. 10).

А (Сберегательные банки Центрального района):

В (Сберегательные банки Партизанского района):

( C ₁ = A И B ) (Сберегательные банки Центрального и Партизанского районов):

Fig. 10. Объединение отношений

Операция Пересечение ( C ₂ = A З B ) предполагает наличие на входе двух отношений одинаковой размерности: А и В. На выходе создается отношение той же структуры, содержащее только те кортежи отношения А, которые есть в отношении В (рис 11).

Отношение А Отношение В Отношение С

Fig. 11. Операция пересечения

Operation Division. Two relations are used at the input of the operation: A and B. Let the relation A, called divisible, contain attributes (A _1, A ₂ , A ₃ , ..., A _n ). The relation B is a divisor and contains a subset of the attributes A: (A _1, A ₂ , ..., A _k ), where k The resulting relation C is defined on the attributes of the relation A, which are not in B, that is, A _{to + 1,} A _{to + 2} , ..., A _n .

Attitude A Attitude In Attitude C

Fig. 12 . Division operation

In general, the operations of the relational data model provide the ability to manipulate relationships, allowing you to update the database, as well as select subsets of stored data and present them in the desired form.

When designing and working with databases, these eight operations are usually not enough. Therefore, such operations are added as: renaming of attributes, formation of new calculated attributes, assignment operations, comparisons, etc.