3. Continuity of function 2.3.1. Continuous and discontinuous functions

Let function 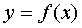defined around the number 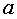. Function 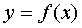called continuous at the point 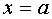, if a:

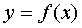• function defined in some neighborhood of a point ;
• .

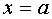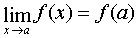Function 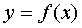called continuous on the interval 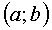if it is continuous at every point of this interval. If they say that the function 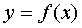continuous on segment 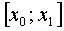, it implies that the function 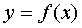continuous at some interval 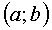containing a segment .

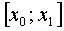Elementary functions are continuous in their domain of definition, more precisely, on the largest open set contained in the domain of definition. For example, the function 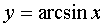defined on the segment [-1; 1], and is continuous on the interval (1; 1).