Lecture
Let be 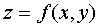 defined on area D. We assume that the argument y is constant and consider the resulting function in one variable x . Give the variable x an increment Δx . Incrementing Δx will cause the function to increment
defined on area D. We assume that the argument y is constant and consider the resulting function in one variable x . Give the variable x an increment Δx . Incrementing Δx will cause the function to increment 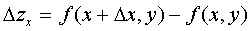 . The final limit of the ratio of the increment of the function Δz x to the increment of the argument Δx at
. The final limit of the ratio of the increment of the function Δz x to the increment of the argument Δx at 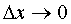 is called a partial derivative of the first order in x and is denoted by
is called a partial derivative of the first order in x and is denoted by 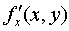 i.e.
i.e. 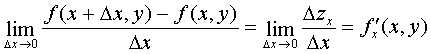 .
.
If we consider the argument x constant and consider the function 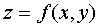 as a function of one variable y , the increment Δy will cause an increment of the function
as a function of one variable y , the increment Δy will cause an increment of the function 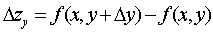 . The final limit of the ratio of the increment of the function Δz y to the increment of the argument Δy at
. The final limit of the ratio of the increment of the function Δz y to the increment of the argument Δy at 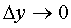 is called a partial derivative of the first order in y and is denoted by
is called a partial derivative of the first order in y and is denoted by 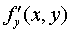 i.e.
i.e. 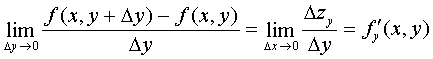 .
.
The symbols are also used to denote partial derivatives: 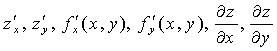 .
.
Partial derivatives of the second order of the function 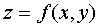 are called partial derivatives of its partial derivatives of the first order:
are called partial derivatives of its partial derivatives of the first order: 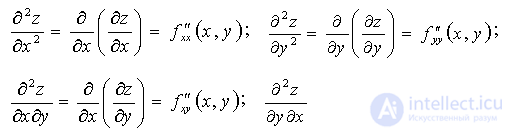 .
.
And 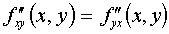 if derivatives are continuous.
if derivatives are continuous.
Derivatives of higher orders are calculated similarly.
Comments
To leave a comment
Mathematical analysis. Differential calculus
Terms: Mathematical analysis. Differential calculus