You get a bonus - 1 coin for daily activity. Now you have 1 coin

2.1. The concept of the limit of function

Lecture



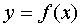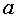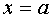Let function 2.1. The concept of the limit of function defined around the number 2.1. The concept of the limit of function (at 2.1. The concept of the limit of function function ƒ may not be defined). The number A is called the limit of the function. 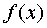2.1. The concept of the limit of function with x tending to 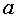2.1. The concept of the limit of function ( 2.1. The concept of the limit of function ), if for any arbitrarily small number ε > 0 there exists a number δ > 0 such that for all x satisfying the condition 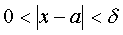2.1. 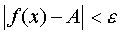The concept of the limit of function inequality holds 2.1. The concept of the limit of function .

Expression 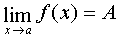2.1. The concept of the limit of function means the limit function 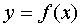2.1. The concept of the limit of function with x tending to 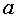2.1. The concept of the limit of function is equal to a.

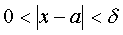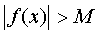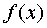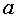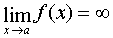If for any arbitrarily large positive number M there is a number δ > 0 such that for all x satisfying the condition 2.1. The concept of the limit of function inequality holds 2.1. The concept of the limit of function then say function 2.1. The concept of the limit of function is infinitely large when x tends to 2.1. The concept of the limit of function and write down: 2.1. The concept of the limit of function .

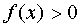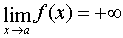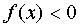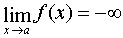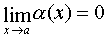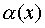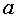If this value 2.1. The concept of the limit of function , then write: 2.1. The concept of the limit of function , what if 2.1. The concept of the limit of function , then write: 2.1. The concept of the limit of function . If a 2.1. The concept of the limit of function then function 2.1. The concept of the limit of function is called an infinitely small value when x tends to 2.1. The concept of the limit of function .

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Mathematical analysis. Differential calculus

Terms: Mathematical analysis. Differential calculus