Lecture
Gradient function 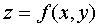 at the point M (x, y) is called a vector with the origin at the point M , with its coordinates the partial derivatives of the function z ,
at the point M (x, y) is called a vector with the origin at the point M , with its coordinates the partial derivatives of the function z , 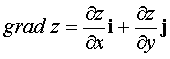 . The symbol for the gradient is often used.
. The symbol for the gradient is often used. 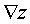 . The gradient indicates the direction of the fastest growth function at a given point.
. The gradient indicates the direction of the fastest growth function at a given point.
Derivative function 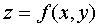 at point M (x, y) in the direction of the vector
at point M (x, y) in the direction of the vector 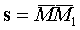 called
called 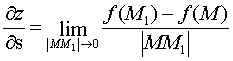 .
.
If the function 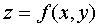 differentiable, then the derivative in this direction is calculated by the formula
differentiable, then the derivative in this direction is calculated by the formula 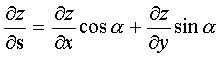 , where α is the angle between the vector s and the axis OX .
, where α is the angle between the vector s and the axis OX .
Using the definition of the gradient, the formula for the derivative in the direction can be given the form: 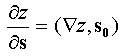 , where the vector s o is the ort of the vector s , i.e. the derivative of the function in this direction is equal to the scalar product of the gradient of the function and the unit vector of this direction.
, where the vector s o is the ort of the vector s , i.e. the derivative of the function in this direction is equal to the scalar product of the gradient of the function and the unit vector of this direction.
Derivative 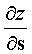 in the direction of the gradient has the greatest value of
in the direction of the gradient has the greatest value of 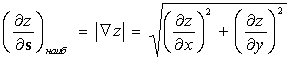 .
.
Comments
To leave a comment
Mathematical analysis. Differential calculus
Terms: Mathematical analysis. Differential calculus