5.3. Extremum functions

Function value 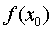called function maximum 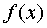, if for any point x from some sufficiently small neighborhood of the point x _o the inequality 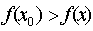. The point x _o is called in this case the maximum point of the function. .

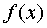Function value 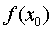called the minimum function 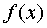, if for any point x from some sufficiently small neighborhood of the point x _o the inequality 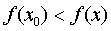. The point x _o in this case is called the minimum point of the function. .

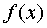The maximum or minimum of a function is called a function extremum . The point of maximum or minimum of a function is called the extremum point of the function .

Necessary condition for the existence of an extremum: if a differentiable function 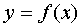reaches an extremum at the point x _o , then its first-order derivative at this point is zero, i.e. .

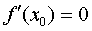Points where the derivative 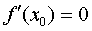or does not exist, are called critical points.

Sufficient condition for the existence of an extremum: if x _o is a critical point of the function and when passing through it, the derivative 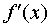changes the sign from plus to minus, then the point x _o is the maximum point, and the value of the function 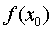- maximum function; if at the transition through the point x _o derivative 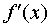changes the sign from minus to plus, then the point x _o is the minimum point, and the value 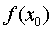- minimum function; if at the transition through the point x _{o the} derivative of the sign does not change, then there is no extremum at the point, and the value 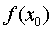not an extremum of function.