Lecture
Let be 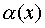 and
and 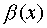 - infinitely small with
- infinitely small with  .
.
If a 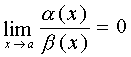 then
then 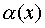 is infinitely small of a higher order compared to
is infinitely small of a higher order compared to 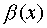 . In this case, it is said that
. In this case, it is said that 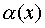 there is " about small" from
there is " about small" from 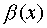 and write down:
and write down: 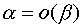 .
.
If a 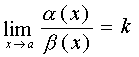 where k is a non-zero number, then
where k is a non-zero number, then 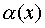 and
and 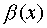 - infinitely small one order . In this case, it is said that
- infinitely small one order . In this case, it is said that 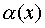 there is " Oh big" from
there is " Oh big" from 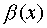 and write down:
and write down: 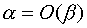 .
.
In the particular case, if 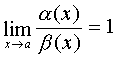 then infinitesimal
then infinitesimal 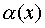 and
and 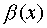 called equivalent and write:
called equivalent and write: 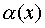 ~
~ 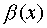 .
.
If a 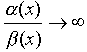 then
then 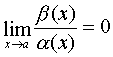 . Consequently,
. Consequently, 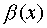 is infinitely small of a higher order compared to
is infinitely small of a higher order compared to 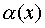 (
( 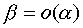 ).
).
In calculating the limits, the following infinitesimal equivalence is often used: 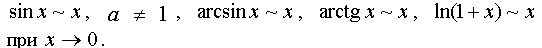
Comments
To leave a comment
Mathematical analysis. Differential calculus
Terms: Mathematical analysis. Differential calculus