Examples of solving problems to the section limits and derivative. differential calculus

Example N 1

Calculate: .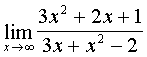

Decision.

The numerator and denominator fraction increase indefinitely with . In this case, it is said that there is a type of uncertainty. 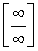. We divide the numerator and denominator of the fraction by the highest power of the variable x , in our case - by x ² :

.

Since when each fraction .

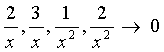Answer: 3

Example N 2

Calculate: .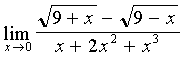

Decision.

The numerator and denominator of the fraction when also tend to zero. In this case, there is a type uncertainty. 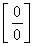. Multiply the numerator and denominator of the fraction by :

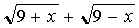Fraction denominator 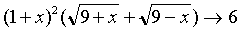at 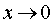, Consequently .

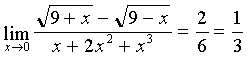Answer: .

Example N 3

Calculate: .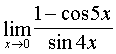

Decision.

We use the trigonometric formula 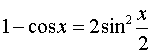and replace the numerator and denominator of the fraction with equivalent infinitesimal 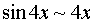and :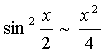

The answer is: 0 .

Example N 4

Calculate: .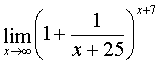

Decision.

With expression 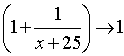, and ( x +7) increases without limit.
In this case, there is a type uncertainty. 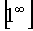. It is recommended to use the second wonderful limit. 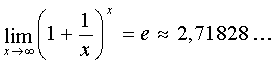or a consequence of it: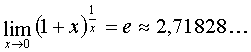

Because 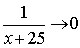at then 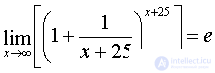. Considering that 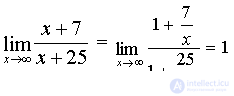(see example N1), we finally get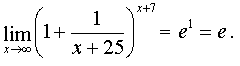

Answer: .

Example N 5

Calculate: .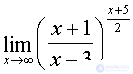

Decision.

Since when expression 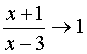type uncertainty takes place 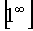. Convert the function to use the second remarkable limit. Select the integer part of the fraction (for this we add to the numerator of the fraction and subtract 3): 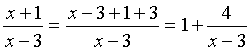then

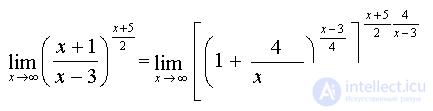
Because 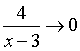at then .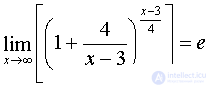

Considering that 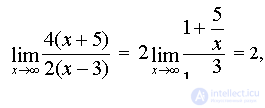finally get: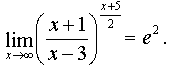

Answer: .

Example N 6

Investigate the function 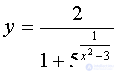on continuity and plot it out graphically.

Decision.

This function has a break in points. 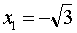and 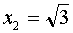, since at these values ​​the denominator of the fraction 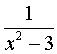vanishes. We investigate the nature of the gap at each of these points.

For this we find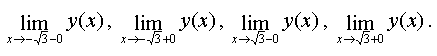

For point :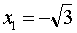

Because
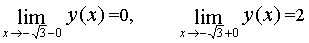and 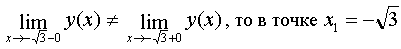then at 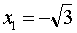the function has a break of the first kind or a jump.

For point :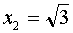

So for the point 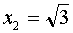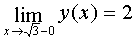and 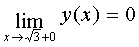it means that 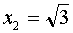the function also suffers a discontinuity of the first kind or a jump. For a schematic plotting of a graph, we investigate the behavior of a function when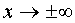

Therefore, when 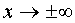the graph of the function is about the straight line y = 1. Find the point of intersection of the graph with the axis of the shelter :

.

Answer: Schematic diagram of the function (Fig. 8):

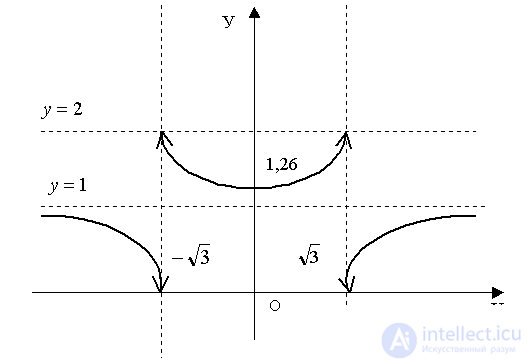
Fig. eight

Example N 7

Find the derivative of the function .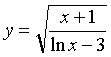

Decision.

Convert square root to the degree: .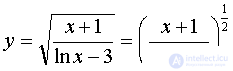

This function is complex, we use successively formulas: the derivative of a power function, the derivative of a fraction, the derivative of the logarithm.

Answer: .

Example N 8

Calculate the derivative of the function .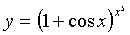

Decision.

This function refers to the type of exponential - power function. 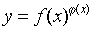. To find its derivative, we prologize this function: .

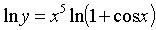Differentiating the left and right sides of this equality, we obtain

Answer: .