Lecture



The classical Fourier transform (continuous and discrete) is a very useful mathematical tool for analyzing and synthesizing signals, but sometimes it is not effective enough to process complex signals. The Fourier transform, for example, does not distinguish between signals from two sinusoids with different frequencies, one of which is the sum of sinusoids, the second - successively following sinusoids. In both cases, their spectrum will look like
two peaks at two fixed frequencies. Consequently, the Fourier transform in its traditional form is not adapted for the analysis of non-stationary signals, including those localized at a certain time interval, since information about the temporal characteristics of the signal is lost.
Therefore, spectral analysis of real signals should be carried out both in frequency and in time. The advantages of this analysis are obvious. In practice, most often we have to deal with non-stationary processes, in which the fact of a change in the frequency-time characteristics of a signal is informative.
To perform such an analysis requires basic functions that have the ability to identify in the analyzed signal, both frequency and its temporal characteristics. In other words, the basic functions themselves must have certain
properties called time-frequency localization
3.1. Time-frequency properties of basis functions
3.1.1. Frequency-time plane
To analyze and compare the time-frequency localization properties of different bases, the frequency-time plane is used. Any function ϕ (t) can be characterized by an interval on the time axis and an interval in the Fourier region, which contain 90% of its energy concentrated near the center of gravity (B.3) of the function. Then, in this plane, the function ϕ (t) can be represented as a rectangle, as shown in Fig. 3.1. It is obvious that the shift of the function by τ from the initial state causes the rectangle to move parallel to the t axis.
As follows from the scaling property of the Fourier transform (2.2.5), the width of the basis function in the time and frequency domains is interrelated: the expansion of the function in the time domain leads to its narrowing in the frequency domain and vice versa.
The pattern that relates these two quantities is called the uncertainty principle.
So, the time-frequency analysis is designed to detect local frequency-time disturbances of the signal. Due to the short duration of such disturbances, the signal itself can be considered as given in L2, i.e. for one-dimensional signals - on the whole real axis R (- ∞, ∞) with the norm
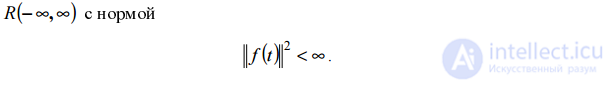
Consequently, the basis functions, which are called wavelets, must also belong to L2 and rapidly decrease as t → ∞. Then, with such basic functions to cover all possible time positions of the signal, it is necessary that the basic functions be a set of functions that are displaced in time. It is most convenient if this set is formed from the same “parent” function ψ (t) (prototype) shifted along the t axis, i.e. {ψ (t - b). } To provide frequency analysis, the base function must have one more argument - the scale factor, which is analogous to the frequency in Fourier analysis. Then the basis functions for time-frequency analysis will look like
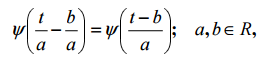
Comments
To leave a comment
Methods and means of computer information technology
Terms: Methods and means of computer information technology