20 Features of image segmentation based on the analysis of contours. Descriptors used to describe the boundaries of objects.

Basic concepts Under the image contour, we mean a spatially extended discontinuity, differential or abrupt change in brightness values. The ideal differential has the properties of the model shown in Fig. 1a, a set of connected pixels, each of which is located next to a rectangular brightness jump, as shown by the horizontal profile in Fig. In reality, optical limitations, discretization, etc. result in blurry brightness drops. As a result, they are more accurately modeled by a sloping profile similar to that shown in Fig. 1b. In such a model, the point of difference in brightness is any point lying on an inclined section of the profile, and the difference itself is a connected set formed by all such points.

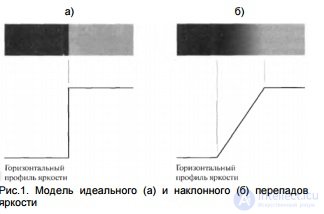
The difference in brightness is considered a contour, if
height and angle of inclination exceed certain thresholds [1-3].
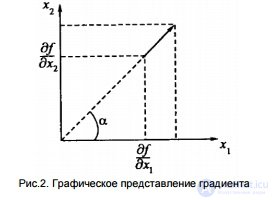
We note a number of problems that arise during contour selection: - contour breaks in places where the brightness does not change quickly enough; - false contours, due to the presence of noise in the image; - excessively wide contour lines due to blurriness, noise, or due to the disadvantages of the algorithm used; - inaccurate positioning due to the fact that the contours of the line of a single, and not zero width. Differential methods One of the most obvious and simple ways to detect boundaries is the differentiation of brightness, considered as a function of spatial coordinates. Detection of contours for an image with brightness values ​​f (x1, x2) perpendicular to the x1 axis ensures the taking of the partial derivative df / dx1, and perpendicular to the x2 axis the taking of the partial derivative df / dx2. These derivatives characterize the rate of change in brightness in the x1 and x2 directions, respectively. To calculate the derivative in an arbitrary direction, you can use the brightness gradient: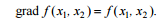
Gradient is a vector in two-dimensional space, oriented in the direction of the fastest increasing function () 1 2 fx, x and having a length proportional to this maximum speed [1].
The gradient module is calculated by the formula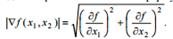
To select the contour of an arbitrary direction we will use the modulus of the gradients of the brightness field. For images instead of derivatives, we take
discrete differences [1,3].

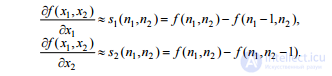
To increase the speed of calculating the modulus of the gradient, we use the following function:

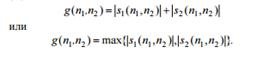
Roberts operator One of the options for calculating a discrete gradient is the Roberts operator. Since the differences in any two mutually perpendicular directions can be used to calculate the modulus of the gradient, the diagonal differences in the Roberts operator are taken:

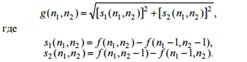
The definition of the difference is formed by two filters with finite impulse response (FIR-
filters), the impulse responses of which correspond to 2x2 masks

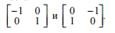
The disadvantages of this operator include high sensitivity to noise and orientation of the area boundaries, the possibility of breaks in the contour and the absence of a pronounced centering
an item. And he has one virtue - low resource intensity

Sobel and Prewitt operators
In practice, it is more convenient to use Sobel and
Previtt. The operator Sobel influence of the noise of the corner elements is somewhat less than that of the operator Prewitt, which is essential when working with derivatives. Each of the masks has a sum of coefficients equal to zero, i.e. these operators will give a zero response in areas of constant brightness [1,3,4].
FIR filters are 3x3 masks.
The Sobel operator uses a weighting factor of 2 for the middle elements. This increased value is used to reduce the smoothing effect by adding more weight to the midpoints.
To address the issue of invariance with respect to rotation, so-called diagonal masks are used to detect gaps in the diagonal directions.


In the presence of a central element and low resource intensity, this operator is characterized by high sensitivity to noise and orientation of the area boundaries, as well as the possibility of gaps in
contour.

Laplacian
To solve the problem of distinguishing brightness differences, you can apply differential operators of a higher order, for example, the Laplace operator [1,3,4]:

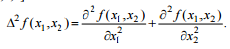
In the discrete case, the Laplace operator can be implemented as a procedure for linear image processing with a 3x3 window. The second derivatives can be approximated by second differences:

Laplacian accepts both positive and negative values, so the absolute value of the contour selection operator must be taken. Thus, we obtain a procedure for the selection of boundaries, insensitive to their orientation:

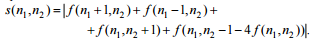
The role of the Laplacian in segmentation problems comes down to using its zero-level intersection property to localize the contour and find out whether the pixel in question is on the dark or light side of the contour. The main disadvantage of the laplacian is the very high sensitivity to noise. In addition, the appearance of gaps in the circuit, as well as their doubling. The advantages of it can be attributed
the fact that it is insensitive to the orientation of the boundaries of the regions, and low resource intensity

Local processing Ideally, border detection methods should only select pixels on the contour in the image. In practice, this set of pixels rarely displays the contour fairly accurately due to noise, discontinuity of the contours due to inhomogeneous illumination, etc. Therefore, contour detection algorithms are usually supplemented with binding procedures to form sets of contour points containing contours. One way to associate contour points is to analyze the characteristics of pixels in a small neighborhood of each image point that has been marked as contour. All points that are similar in accordance with some criteria are connected and form a contour consisting of pixels that meet these criteria. It uses two main parameters to establish the similarity of the contour pixels: the magnitude of the response of the gradient operator, which determines the value of the contour pixels, and the direction of the gradient vector. A contour pixel (x0, y0) located inside a given neighborhood of a point (x, y) is considered to be similar in magnitude to a pixel (x, y) in magnitude if

. A pixel in a given neighborhood is combined with a central pixel (x, y) if the similarity criteria are met both in magnitude and in direction.
This process is repeated at each point of the image while simultaneously memorizing the found connected pixels as the center moves.
A simple way to account for data is that each set of contour pixels to be linked
its brightness value is assigned [3].

Canny Boundary Detector

The Canny Boundary Detector [5] focuses on three main criteria: good detection (increase in signal-to-noise ratio); good localization (correct positioning of the boundary); the only response to one border. From these criteria, the objective function of the cost of errors is constructed, the minimization of which is the “optimal” linear operator for convolution with the image. To reduce the sensitivity of the algorithm to noise, the first derivative of the Gaussian is applied. After applying the filter, the image becomes slightly blurred. This is how the Gaussian mask looks like:

After calculating the gradient of the smoothed image in the boundary contour, only the maximum gradient points of the image are left. Information is used on the direction of the border in order to remove points near the border and not to break the border itself near the local maxima of the gradient [5]. To determine the direction of the gradient, the Sobel operator is used. The obtained values ​​of the directions are rounded to one of the four corners - 0, 45, 90 and 135 degrees. Then, using two thresholds, weak boundaries are removed. Fragment of the border is treated as a whole. If the value of the gradient somewhere on the traceable fragment exceeds the upper threshold, then this fragment also remains the “permissible" border in those places where the gradient value falls below this threshold until it falls below the lower threshold. If there is not a single point on the entire fragment with a value above the upper threshold, then it is deleted. Such a hysteresis reduces the number of breaks in the output limits.
The inclusion of noise reduction in the algorithm increases the stability of the results, but increases computational costs and leads to distortion and loss of border details. The algorithm rounds the corners of the objects and destroys the boundaries at the junction points.
The disadvantages of this method are the complexity of implementation and the very large resource consumption, as well as the fact that some rounding of the corners of the object is possible, which leads to a change in the parameters of the contour. The advantages of the method include the low sensitivity to noise and orientation of the boundary areas, the fact that it clearly identifies the contour and allows you to identify the internal contours of the object. In addition, it eliminates the erroneous detection of counter-attacks, where there are no objects.

Analysis using graph theory The approach to detecting and linking contours based on graph representation and searching for least-cost paths on this graph allows us to construct a method that works well in the presence of noise. This procedure is quite complicated and requires more processing time.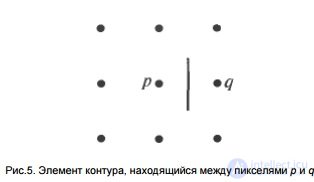


The contour element is the boundary between two pixels p and q, which are neighbors. Contour elements are identified by coordinates of the points p and q. The contour element in Fig. 5 is determined by the pairs (xp, ur) (xq, yq). Contour - a sequence of contour elements connected to each other. Each contour element defined by pixels p and q corresponds to a certain value, which is defined as c (p, q) = H - [f (p) - f (q)],

where H is the maximum brightness level in the image, af (p) and f (q) are the values
brightness pixels p and q, respectively.
The task of finding the minimum cost path on a graph is nontrivial in calculating
complexity, and you have to sacrifice optimality in favor of the speed of calculations [3].
The complexity of implementation and high resource consumption - these are the main disadvantages of such an analysis, the advantage of which is the low sensitivity to noise.


Signs of images.
Two significant problems in pattern recognition are the following: what input data can be considered relevant and what preliminary processing of the initial data (usually characterized by extreme redundancy) results in properties or attributes that actually allow classification.
Depending on the specifics of the task, many types of features are used.
Local Descriptors. Descriptors are a structure describing the properties of an object.
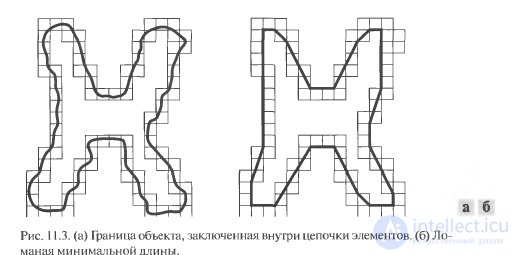
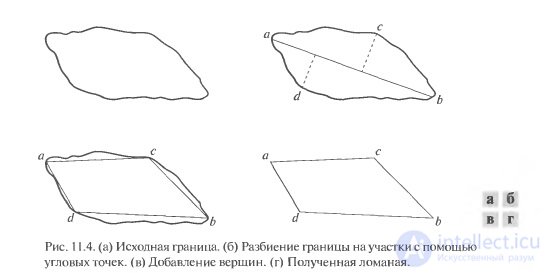
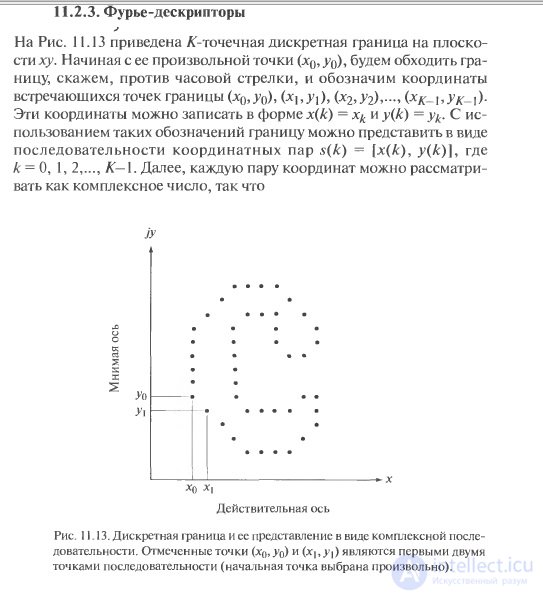
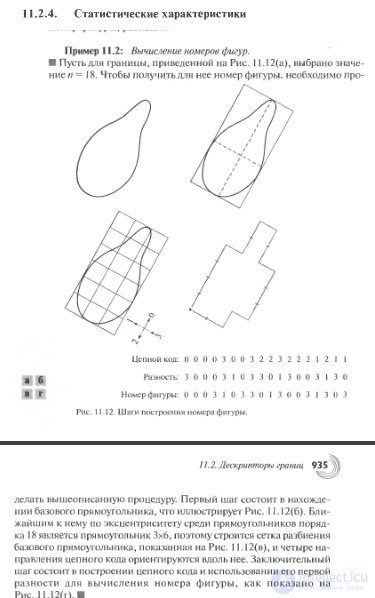
Border Descriptors. The area that is of interest can be described by the shape of its boundary or by setting its characteristics. Boundary descriptors include a number of the most common methods: chain codes, signatures, and polygon approximation.
Region Descriptors. Area area is defined as the number of pixels contained within its boundary. This descriptor is useful in collecting information about the relative position and shape of objects from which the camera is located at approximately the same distance.
Handles key points . The result of the detectors is a set of singular points for which it is necessary to construct a mathematical description. The input to the descriptor is an image and a set of singular points selected on a given image. The output of the descriptor is a set of feature vectors for the initial set of special points.