Lecture
One of the main ways to process speech in the frequency domain is short-term spectral analysis. The performance of many speech recognition systems, spectrographs, vocoders is based on short-term spectral analysis. Short-term spectral analysis can be implemented using a comb of bandpass filters (Fig. 2) or using a discrete Fourier transform. Filter bandwidths are selected to cover the entire frequency range of speech. The average values of the modules of the output signals of the filters will represent the values of the spectral coefficients in the bands.
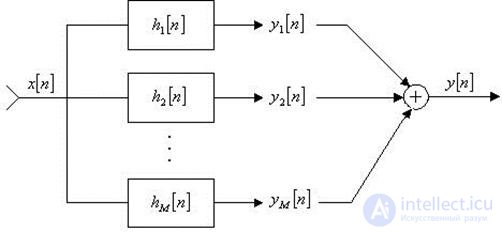
Fig. 2. Comb filters.
Sometimes the frequency range is divided into unequal bands, taking into account the peculiarities of the human hearing. It was established experimentally that in the inner ear of a person the pitch (frequency) of the sound signal is converted into mechanical vibrations of certain sections of the basilar membrane. In this case, linear increments of the coordinate along the membrane body correspond to logarithmic increments of the sound frequency, i.e. the frequency of a sound perceived by a person non-linearly depends on the actual physical frequency. This leads to unequal resolution in frequency and to the perception of sounds in accordance with the mechanism of critical frequency bands . A complex sound of constant loudness, consisting of several tones lying within the critical band, is perceived by a person with the same subjective feeling as a single-tone sound corresponding to the center frequency of the critical band. The width of the critical bands for the frequency range up to 500 Hz is approximately 100 Hz. Above 500 Hz, the width of the critical bands increases by about 20% compared with the width of the previous band. The width of the critical bands is approximated by the dependence: 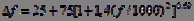
[Hz].
To characterize the subjective frequencies perceived by man, several scales have been proposed: a bark scale , a chalk scale . Function
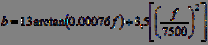 [Barque]
[Barque]
used to translate frequencies given in hertz into barges.
A comb (bank) of filters with unequal bandwidths, set in Hertz and corresponding to critical hearing bands, will have a uniform distribution of center frequencies and equal values of bandwidths measured in barks. Thus, the use of the bark scale corresponds to a uniform division of the axis of subjective frequencies. The chalk scale is introduced with a similar purpose and has minor differences from the bark scale.
Short-term spectral analysis of speech can also be performed on the basis of the DFT. Short-term discrete Fourier transform is defined as follows:
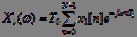 , (3)
, (3)
Where 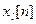 represents a segment of speech weighted by a window
represents a segment of speech weighted by a window  long
long  counts:
counts:
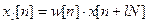 ,
, 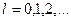 (four)
(four)
One of the algorithms for determining the pitch frequency is based on the calculation of the product:
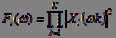 . (five)
. (five)
The values calculated using (5) can be quite large. To reduce the values, the logarithm of (5) is calculated. Dependence represents the product of functions compressed in frequency. In vocalized speech, the frequency compression in times should lead to the coincidence of the harmonics of the fundamental tone. Due to this, a maximum at the frequency of the fundamental tone appears in the spectrum. Unvocalized speech is characterized by significantly lower values and it does not have a maximum in the spectrum at the frequency of the fundamental tone. This method of determining the frequency of the fundamental tone is resistant to noise, since the noise components in the spectrum are not regular.
Homomorphic speech processing.
The speech signal is a convolution of the excitation function (random noise or a quasi-periodic sequence of pulses) and the impulse response of the vocal tract. Homomorphic speech analysis allows you to separate these components. Therefore, using homomorphic analysis, it is possible to determine the period of the fundamental tone and the frequency properties of the vocal tract. The general scheme of homomorphic processing is shown in Fig. 3

Fig. 3. General scheme of homomorphic processing.
In accordance with this scheme, a non-linear transformation is first performed.  signal
signal 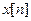 which is determined by the relation:
which is determined by the relation:
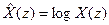 . (6)
. (6)
Then an operator is executed that corresponds to a linear invariant system. At the end of the transformation is implemented.
Let the signal 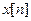 is a convolution of two sequences
is a convolution of two sequences 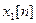 and
and 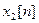 . Then:
. Then:
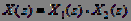 . (7)
. (7)
Substituting (7) in (6), we get:
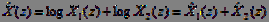 . (eight)
. (eight)
The linear invariant system passes only one of the components to the output. 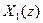 or
or 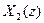 . Accordingly, the inverse transform gives
. Accordingly, the inverse transform gives 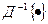 or
or 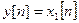 . Consequently, homomorphic processing separates the input components.
. Consequently, homomorphic processing separates the input components. 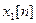 and
and 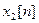 contained in the input signal.
contained in the input signal.

Fig. 4. Homomorphic speech analysis system.
The homomorphic speech analysis system is shown in fig. 4. Here, at the first stage, the logarithm of the module of the transient Fourier transform is calculated. If we assume that the signal at point A is a convolution of the excitation function and the impulse response of the vocal tract, then at C, we obtain the sum of the logarithms of the excitation function spectrum and the impulse response of the vocal tract. The signal at point D, obtained using the inverse discrete Fourier transform, is called a cepstrom . A cepstrum at point D is equal to the sum of the capstres of the excitation function and the impulse response of the voice trust.
Kepstr - Energy Spectrum Function 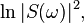 defined by expression
defined by expression 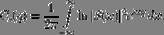
In other words, the cepstrum determines the sequence of coefficients of the expansion of the function log [Φ (z)] in a power series.
The argument q has the dimension of time, but this is a special, cepstral time, because at any moment q depends on the function of the original signal with the spectrum 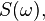 given at
given at 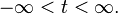 Sometimes q is called “Sactot” or “Kyufrensi” (anagrams from Russian. Frequency or English frequency ).
Sometimes q is called “Sactot” or “Kyufrensi” (anagrams from Russian. Frequency or English frequency ).
In English, there are two analogues of this concept - Kepstrum and Cepstrum .
1. Short-term Fourier transform of a one-dimensional signal. Time-frequency analysis of signals.
Comments
To leave a comment
Methods and means of computer information technology
Terms: Methods and means of computer information technology