Lecture
Image segmentation is the division of an image into regions that are unlike in a certain attribute. It is assumed that the areas correspond to real objects, or their parts, and the boundaries of the areas correspond to the borders of the objects. Segmentation plays an important role in image processing and computer vision tasks.
11.3. Region handles
In this section, we will look at the various approaches used to describe image areas. Recall that a common practice is to use a combined description that includes descriptors of both borders and areas.
1. Some simple descriptors
Area area is defined as the number of pixels that it contains. The perimeter of the area is the length of its boundary. Although the area and perimeter are sometimes used as descriptors, this applies mainly to those cases where the sizes of the regions of interest do not change. More often, these descriptors are used in calculating the measure of compactness of an area, which is defined as the ratio of the square of the perimeter to the area. Compactness is a dimensionless quantity (and therefore invariant to homogeneous scale changes), which assumes a minimum value for a region of a circular shape. Up to inaccuracy, when rotating discrete areas, compactness is also invariant to the orientation of the object.
Other simple descriptors used to describe areas include the average value and the median of the brightness of the area elements, as well as the number of pixels with brightness values greater or less than the average value.
Example 11.4: Retrieving information from an image using area calculation.
I Even such a simple area descriptor, like the normalized area, can be very useful for extracting information from images. Consider as an example. 11.16, where the infrared satellite image of the American continent. As already described in detail in Section 1.3.4, such images allow you to maintain a global record of human settlements. The sensors used to register such images are sensitive to radiation in the visible and near-infrared ranges and allow you to record light and fire, including short-duration flashes. The table in the figure shows the relations of the white area (illuminated areas) by region to the total illuminated area in all four regions. Even such simple measurements allow, for example, to obtain relative estimates of energy consumption by region. These data can be clarified by rationing in relation to the land area in the region, population, etc. |
.2. Topological Descriptors
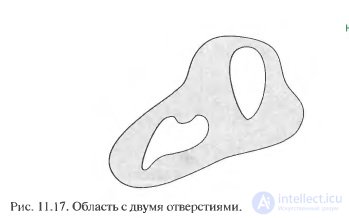
For the global description of areas on the image plane, their topological properties are often useful. In general terms, topology studies the properties of figures that are not affected by any deformation, if there are no breaks and glueing (as if the image plane behaves similarly to a sheet of rubber). For example, in Fig. Figure 11.17 shows the area with two holes inside. If the number of holes inside a region is used as a topological descriptor, then this property will obviously be invariant with respect to stretching or rotation. However, generally speaking, the number of such holes will change if the area collapses or breaks. Note that although at stretching and the distances between the points of the region change, the topological properties do not depend on the concept of distance, nor on any other properties implicitly based on the measurement of distances.
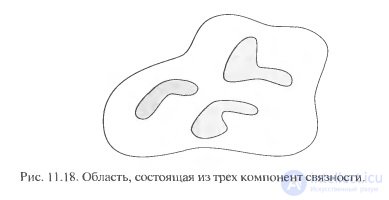
Another topological property useful in describing a region is the number of its connected components. The definition of the domain connectivity component was given in Section 2.5.2. In Fig. 11.18 shows the region consisting of three components of connectivity (Cm. Section 9.5.3, where the algorithm of separation of connected components was considered).
The number of holes H and the number of connected components C of a certain figure are used in determining its Euler number E:
E = C – H (11.3-1)
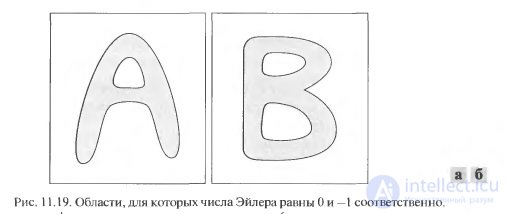
The Euler number is also a topological property. For example, shown in Fig. 11.19 areas are characterized by Euler numbers O and - 1, respectively, since the area "A" consists of one connected component and contains one hole, and the area "B" also consists of one connected component, but contains two holes.
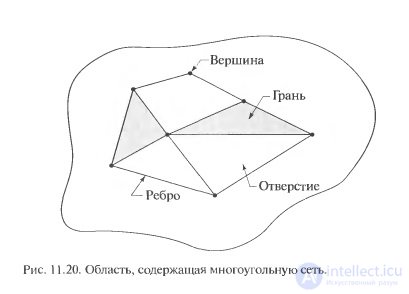
The regions formed by straight line segments (such areas are usually called polygonal networks) admit a particularly simple interpretation in terms of the Euler number. In Fig. 11.20 shows an example of a polygonal network. The interior of such polygonal networks is often important to classify as faces or holes. The known V is the number of vertices of the network, Q is the number of its edges, and F is the number of faces, we write the following relation, called the Euler formula:
V-Q + F = CH. (11.3-2)
Given the definition (11.3-1), both sides of this equality are equal to the Euler number:
V -Q + F = C- H = E. (11.3-3)
The network shown in Fig. 11.20, there are 7 vertices, 11 edges, 2 faces, 1 connected component and 3 holes; therefore, the Euler number is -2:
7-11 + 2 = 1-3 = -2.
(supplement Image segmentation based on uniformity)
Image segmentation is the division of an image into regions that are unlike in a certain attribute. It is assumed that the areas correspond to real objects, or their parts, and the boundaries of the areas correspond to the borders of the objects. Segmentation plays an important role in image processing and computer vision tasks.
Tasks of automatic segmentation are divided into two classes:
selection of image areas with known properties
image splitting into homogeneous areas
There is a fundamental difference between these two problem statements. In the first case, the segmentation task is to search for specific areas about which there is a priori information (for example, we know the color, the shape of the areas, or the areas of interest are images of a known object). The methods of this group are narrowly specialized for each specific task. Segmentation in this formulation is used mainly in problems of computer vision (scene analysis, search for objects in the image).
In the second case, no a priori information about the properties of the regions is used, but some conditions are imposed on the image splitting itself (for example, all regions should be uniform in color and texture). Since in such a formulation of the segmentation problem, a priori information about the depicted objects is not used, the methods of this group are universal and applicable to any images. Basically, the segmentation in this formulation is applied at the initial stage of solving the problem in order to get a representation of the image in a more convenient form for further work. For a rough assessment of the quality of a method in a particular problem, several properties are usually fixed, which a good segmentation should possess. The quality of the method is evaluated depending on how well the segmentation obtained has these properties. The following properties are most commonly used [1]:
- uniformity of regions (uniform color or texture)
- non-similarity of neighboring regions
- smooth region border
- a small number of small “holes” within the region, etc.
Comments
To leave a comment
Methods and means of computer information technology
Terms: Methods and means of computer information technology