Lecture
Analysis of binary images includes the operations used in binary computer vision, for example, particle analysis, processing of documents, fish counting, and in the analysis of half-tone images. It assumes the formation and processing of binary images, usually images, the brightness of the elements of which have the values 0 or 1, with 0 representing the background, 1 representing the object.
The first operation of binary analysis is to select objects on the background from a variety of other objects. Only then is the merging of the image elements of each object, as shown in Figure 7.1 b). After receiving a binary image of the object
possible to calculate the characteristics of the object.
Selection of signs by which you can select an object from the background. In connection with this, before binary operations, halftone and transformations are performed, allowing to enhance the attributes of the object. The next task is related to determining the thresholds for performing binarization. Threshold binarization of half-tone images in accordance with the amplitude characteristics discussed in Section 5.3, allows obtaining a binary image of an object. Figure 7.2 shows an example of binarization of a color image. Since the distinctive characteristic of an object in this example is the red color of the flower and the green color of its legs, the binarization
can be produced by Cb component. Figure 7.3 shows the modal histogram of the Cb values of the component of the original image. One mode corresponds to a flower (values ≤ 115), the other to the background.
The binary image inevitably includes areas caused by interference, so operations have been developed to eliminate or reduce the effect of interference. These operations are related to the morphological operations of binary images. They allow you to separate the United
Objects or connect the broken parts of the object, fill holes in the areas of the object, exclude individual noise objects. After performing such operations on the resulting binary image, an operation called selection of connected components is performed
allowing to represent each individual spatially related object by number.
With a binary image, each connected area can be identified and analyzed. The input image for the operation "selection of connected components" is a binary image. The image of area marks is formed on the output. Each image count
the value of the number of the connected domain to which it belongs, or the zero value, if the element belongs to the background. The operation makes it possible to exclude from consideration areas that have areas that are outside the specified limits of the objects of interest. AT
image processing, this leads to the formation of a halftone image, each brightness level of which corresponds to the number of the connected region (object). According to the image of connected components and the original half-tone image, the evaluation of the signs
Images. In the given example, 202 objects were detected. Objects with an area of less than 17 elements are excluded as belonging to noise.
Finally, the final operation required to perform a binary analysis is to evaluate the characteristics of an object. Figure 7.4 shows a fragment of the brightness and geometric characteristics of the selected orange cells, shown in Figure 7.1.c). Geometric characteristics include: Xc.t., Y.t.t. - The coordinates of the center of gravity of the object, Square. - the area of the object, Perim. -
object perimeter, coeff. forms - form coefficient, estimated as the ratio of the square of the perimeter of the object's area to its area, Dmin, Dmax, Ecc., Angle - characteristics of the scattering ellipse: the size of its small major axes, eccentricity, estimated as the ratio of the minor axis
ellipse to a large, and the angle of inclination of the major axis. Luminance characteristics are represented by the average brightness value in the area of the Luminosity brightness in this area.
Mathematical morphology is defined as operations by supersets. The morphology of binary images is intended for processing areas obtained after performing quantization.
images on two levels. The morphology of binary images consists of two main operations: dilatation (expansion), erosion (reduction) and their derivatives, closing (closing) and
opening (opening).
Signs of areas
After completing the selection of connected regions on the binary image, allowing to mark each region, the signs of these regions are formed. These include the following
features: geometric features, shape characteristics; brightness characteristics; color characteristics; textural properties; sign of movement.
Geometric characteristics include such characteristics as the area, center of gravity, coordinates describing the rectangle and perimeter [48]. The area is equal to the number of image elements belonging to the area. Denote the set of single samples g (x, y) with coordinates (x, y) belonging to the area A, given in the image plane as
Basic definitions
The term morphology refers to the description of the properties of the form and structure of any objects. In the context of machine vision, this term refers to the description of the properties of the shape of regions in an image. The operations of mathematical morphology were originally defined as operations on sets, but it soon became clear that they were also useful in the tasks of processing a set of points in a two-dimensional space. Objects in the image are represented by sets in mathematical morphology. It is easy to notice that the set of all background pixels of a binary image is one of the options for its full description.
First of all, mathematical morphology is used to extract some properties of an image that are useful for its presentation and description. For example, contours, skeletons, convex hulls. Also of interest are the morphological methods used at the stages of preliminary and final image processing. For example, morphological filtration, thickening or thinning.
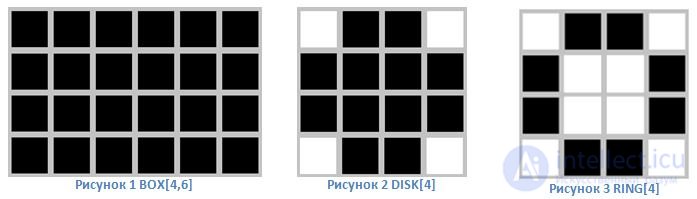
The input data for the apparatus of mathematical morphology are two images: processed and special, depending on the type of operation and the problem being solved. Such a special image is called primitive or structural element. As a rule, the structural element is much smaller than the processed image. A structural element can be considered a description of a region with some form. It is clear that the form can be any, as long as it can be represented as a binary image of a given size. In many image processing packages, the most common structural elements have special names: BOX [H, W] - a rectangle of a given size, DISK [R] - a disk of a given size, RING [R] - a ring of a given size.
The result of morphological processing depends both on the size and configuration of the original image, and on the structural primitive.
The size of the structural element is usually 3 * 3, 4 * 4 or 5 * 5 pixels. This is due to the main idea of morphological processing, in the process of which the characteristic details of the image are sought. The required detail is described by a primitive, and as a result of morphological processing, you can emphasize or delete such details on the entire image.
One of the main advantages of morphological processing is its simplicity: we get a binarized image both at the entrance and at the exit of the processing procedure. Other methods, as a rule, first receive a halftone from the original image, which is then reduced to a binary one using the threshold function.
Basic operations on binary images
The main operations of mathematical morphology are building up, erosion, closure and opening. These names reflect the essence of operations: building increases the image area, and erosion makes it smaller, the closing operation allows you to close the internal openings of the area and eliminate bays along the border of the area, the opening operation helps to get rid of small fragments protruding outside the area near its border. Next will be presented the mathematical definitions of morphological operations.
Union, intersection, addition, difference
Before proceeding to the operations of morphology, it makes sense to consider the set-theoretic operations that underlie mathematical morphology.
The union of two sets A and B, which is denoted by C = A∪B, is, by definition, the set of all elements belonging to either the set A, or the set B, or our sets at the same time. Similarly, the intersection of two sets A and B, which is denoted by C = A∩B, is by definition the set of all elements belonging simultaneously to both sets A and B. The complement of set A is the set of elements not contained in A: A c = {w | w ∉A}. The difference of two sets A and B is denoted A \ B and is defined as follows: A \ B = {w│w∈A, w∉B} = A∩B c . This set consists of elements A which are not included in set B.
Consider all of the above operations on a specific example. 
Transfer
The operation of transferring X t of a set of pixels X to a vector t is given in the form X t = {x + t | x∈X}. Consequently, the transfer of a set of single pixels on a binary image displaces all the pixels of a set by a specified distance. The transfer vector t can be specified as an ordered pair (∆r, ∆c), where ∆r is the transfer vector component in the row direction, and ∆c is the transfer vector component in the column direction of the image. 
Build-up, erosion, closure, opening
The following operations we will look at a specific example. Suppose we have the following binary image and structural element: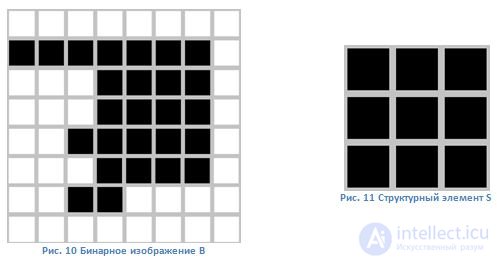 
Building up
The structural element S is applied to all pixels of the binary image. Each time when the origin of the structural element is combined with a single binary pixel, the transfer and the subsequent logical addition with the corresponding pixels of the binary image are applied to the entire structural element. The results of logical addition are written to the output binary image, which is initially initialized to zero values. 
Erosion
When performing an erosion operation, the structural element also passes through all the pixels of the image. If at some position each unit pixel of the structural element coincides with the unit pixel of the binary image, then the logical addition of the central pixel of the structural element with the corresponding pixel of the output image is performed.
As a result of applying the erosion operation, all objects smaller than the structural element are erased, objects connected by thin lines become disconnected and the sizes of all objects decrease. 
Breaking
The erosion operation is useful for removing small objects and various noises, but this operation has a drawback - all the remaining objects are reduced in size. This effect can be avoided if, after an erosion operation, a build-up operation is applied with the same structural element.
Breaking out all objects that are smaller than the structural element, but at the same time helps to avoid a strong reduction in the size of objects. Also, the opening is ideal for removing lines whose thickness is less than the diameter of the structural element. It is also important to remember that after this operation the contours of the objects become smoother. 
Short circuit
If we first apply the extension operation to the image, then we will be able to get rid of small holes and crevices, but at the same time there will be an increase in the contour of the object. To avoid this increase allows the operation of erosion, performed immediately after building with the same structural element. 
Conditional build-up
One of the typical applications of binary morphology is the selection of components on a binary image, in which the shape and dimensions satisfy the specified constraints. In many such tasks, it is possible to build a structural element that, after being applied to the binary image, removes the components that do not satisfy the constraints and leaves several single pixels corresponding to the components that satisfy the constraints. But for subsequent processing may require components entirely, and not only their fragments remaining after erosion. To solve this problem, a conditional expansion operation was introduced.
The set obtained as a result of erosion is cyclically increased by the structural element S, and at each step the result is reduced to a subset of pixels that have single values in the original image B. The conditional extension operation is explained in the figure below. In this figure, the binary image B was eroded by the element V to select components containing vertical fragments 3 pixels in height. The resulting C image has two such components. To select these components entirely, the image C is conditionally expanded by the element D relative to the original image B. 
Selection of boundaries
Morphological operations can also be used to highlight the boundaries of a binary object. This operation is very important, because the border is a complete, and at the same time, a very compact description of the object.
It is easy to see that the boundary points have at least one background pixel in their neighborhood. Thus, applying the erosion operator with a structural element containing all possible neighboring elements, we will remove all boundary points ... Then the boundary will be obtained using the operation of the set difference between the original image and the image obtained as a result of erosion. 
Thus, we have reviewed the basic operations of mathematical morphology, and several ways to apply them. I hope this device will be useful to you in further activities.
Mathematical morphology (MM) - (morphology from the Greek. Μορφή "form" and λογία "science") - the theory and technique of analysis and processing of geometric structures, based on set theory, topology and random functions. It is mainly used in digital image processing, but can also be applied on graphs, polygonal mesh, stereometry, and many other spatial structures.
1 binary morphology
o 1.1 Structural element
o 1.2Basic operations
§ 1.2.1 Basic operations
§ 1.2.1.1 Transfer
§ 1.2.1.2 Growing
§ 1.2.1.3 Erosion
§ 1.2.2 Derivative operations
§ 1.2.2.1. Conclusion
§ 1.2.2.2 Unlocking
§ 1.2.3Conditional escalation
§ 1.2.4 Allocation of boundaries
Binary morphology]
In binary morphology, a binary image represented as an ordered set (ordered set) of black and white dots (pixels), or 0 and 1. An image area is usually understood as a subset of the image points. Each operation of binary morphology is a transformation of this set. A binary image B and some structural element S are taken as the source data. The result of the operation is also a binary image.
Structural element
The structural element is a binary image (geometric shape). It can be of any size and arbitrary structure. The most commonly used symmetric elements, like a rectangle of fixed size (BOX (l, w)), or a circle of a certain diameter (DISK (d)). Each element is allocated a special point, called the initial (origin). It can be located anywhere in the element (and outside of it [1] ), although in symmetrical it is usually the central pixel.
The most common structural elements are: BOX [H, W] is a rectangle of a given size, DISK [R] is a disk of a given size, RING [R] is a ring of a given size.
Basic operations
At the beginning, the resulting surface is filled with 0, forming a completely white image. Then probing or scanning the source image pixel by pixel is carried out. In order to probe each pixel, a structural element is “superimposed” on the image so that the probed and initial points are combined. Then a certain condition is checked for the correspondence of the pixels of the structural element and the image points “under it”. If the condition is satisfied, then the resulting image in the appropriate place is set to 1 (in some cases, not one single pixel will be added, but all the ones from the structural element).
According to the above scheme, the basic operations are performed. Such operations are expansion and contraction. Derived operations are a combination of basic operations that are performed sequentially. The main ones are the opening and closing.
Basic operations ]
Transfer [
Transfer example at t = (2,1).
Операция переноса X t множества пикселов X на вектор t задаётся в виде X t ={x+t|x∈X}. Следовательно, перенос множества единичных пикселов на бинарном изображении сдвигает все пикселы множества на заданное расстояние. Вектор переноса t может задаваться в виде упорядоченной пары (∆r,∆c), где ∆r — компонент вектора переноса в направлении строк, а ∆c — компонент вектора переноса в направлении столбцов изображения.
Наращивание
Наращивание бинарного изображения A структурным элементом B обозначается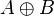 
и задается выражением: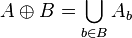 
.
In this expression, the join operator can be considered an operator used in the neighborhood of the pixels. Structural element B is applied to all pixels of the binary image. Every time when the origin of the structural element is combined with a single binary pixel, the transfer and the subsequent logical addition (logical OR) with the corresponding pixels of the binary image is applied to the entire structural element. The results of logical addition are written to the output binary image, which is initially initialized to zero values.
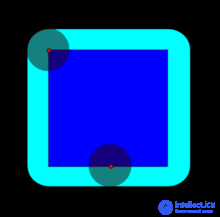
The buildup of a dark blue square is a disk structural element, resulting in a bright blue square with rounded ends.
Erosion [
The erosion of the binary image A with the structural element B is indicated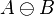 
and specified by the expression: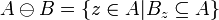
.
При выполнении операции эрозии структурный элемент тоже проходит по всем пикселам изображения. Если в некоторой позиции каждый единичный пиксел структурного элемента совпадет с единичным пикселом бинарного изображения, то выполняется логическое сложение центрального пиксела структурного элемента с соответствующим пикселом выходного изображения. В результате применения операции эрозии все объекты, меньшие чем структурный элемент, стираются, объекты, соединённые тонкими линиями становятся разъединёнными и размеры всех объектов уменьшаются.
Эрозия темно синего квадрата дисковым структурным элементом, результирующего на ярко-голубой квадрат.
Производные операции
Замыкание
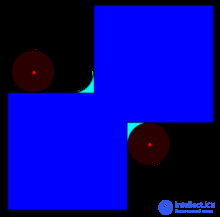
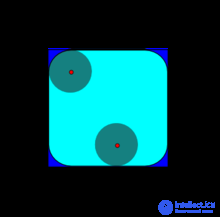
Замыкание темно синей формы (объединение двух квадратов) дисковым структурным элементом, результирующего на темно синюю форму и светло-голубые площади.
Замыкание бинарного изображения А структурным элементом В обозначается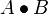 
и задается выражением: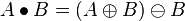 
.
Операция замыкания «закрывает» небольшие внутренние «дырки» в изображении, и убирает углубления по краям области. Если к изображению применить сначала операцию наращивания, то мы сможем избавиться от малых дыр и щелей, но при этом произойдёт увеличение контура объекта. Избежать этого увеличения позволяет операция эрозия, выполненная сразу после наращивания с тем же структурным элементом.
Размыкание
Размыкание темно-синего квадрата дисковым структурным элементом, результирующего на светло синий квадрат с закругленными углами.
Размыканием бинарного изображения А структурным элементом В обозначается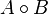 
и задается выражением: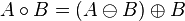 
.
Операция эрозии полезна для удаления малых объектов и различных шумов, но у этой операции есть недостаток — все остающиеся объекты уменьшаются в размере. Этого эффекта можно избежать, если после операции эрозии применить операцию наращивания с тем же структурным элементом. Размыкание отсеивает все объекты, меньшие чем структурный элемент, но при этом помогает избежать сильного уменьшения размера объектов. Также размыкание идеально подходит для удаления линий, толщина которых меньше, чем диаметр структурного элемента. Также важно помнить, что после этой операции контуры объектов становятся более гладкими.
Условное наращивание
Выделение границ
Форма (синяя) и её морфологическое расширение (зеленое) и сужение (желтое) ромбическим структурным элементом.
Comments
To leave a comment
Methods and means of computer information technology
Terms: Methods and means of computer information technology