Lecture
In this section, we will examine some of the practical application of the Principles and Rules of this chapter.
? Holistic projects. Suppose you have an intention to create and implement a project of an engineering device. Then you need an idea - the basic principle of building such a device. To create such an idea will help the methodology of the system philosophy, which includes the constructive principle of consistency. Then you need a theory to implement your idea. To put together all the theoretical results available in this area, and turn them into a holistic theory of the implementation of your idea will help you method of system philosophy. Then you need a project to implement your idea based on the theory obtained. The system technology method will help you to create a holistic project for the implementation of your theoretical ideas on how to implement your idea. And finally, the system technology of activities will help to create a holistic implementation of the project. Consider this example in more detail.
Such a sequence "methodology - theory - design - implementation" is always necessary for the activity to be successful. The system philosophy helps to make it complete, embodying the provisions and postulates of the holistic method of system technology. With the help of the system philosophy, all 4 questions can be worked out in a holistic complex: “How can the intention be transformed into an idea?”, “How to create a theory for the implementation of an idea?”, “How to create a holistic project for the realization of a theory?” project? ”.
? If you neglect the clarity of the idea,
or consider that methodology and theory are useless and need to be closer to practice, or you have the conviction that you can accomplish everything without a project,
or you think that you can accomplish your intention without a clear idea, theory and project,
- better not to get down to business. You are waiting for a temporary success, based on your past methodological and theoretical knowledge. Why temporary?
Because your existing knowledge is not brought into a holistic and whole system, designed to implement exactly this intention of yours. Because no one brings all the methodologies and theories you need into the system, especially into a complete system, for the realization of this idea of yours. Your idea has peculiarities, in connection with which it is necessary to take everything you need from different methodologies and theories and it is necessary to supplement it to a sufficient volume and bring it into a complete system. And this can be done only with the help of a system philosophy.
? The provisions of the system philosophy can be applied to solve mathematical problems.
Consider an example of a system solution technology for the well-known “traveling salesman problem” (OCR) [41] . This example was chosen for the simple reason that it combines the simplicity and clarity of the formulation of the problem with the difficulty of finding an exact or practical solution.
Staging ZOK is as follows. There are n points, one of which is a traveling salesman. The salesman must visit all these points and return to the starting point for a report. The distances between them are known. It is required to find a traveling salesman route, at which the total distance that he will travel will be the shortest of all possible. This task is constantly solved by any traveler who is going to visit several cities. Instead of distances between cities, you can take the fare of those types of transport that can be used when moving from one city to another. Instead of cities, there may be technological cycle operations, and instead of distances, the time required to move from one operation to another. Many tasks of management, economics, planning and organization are reduced to the task of a traveling salesman. It is almost impossible to solve the AOK by large enumeration for large n , since the number of possible solutions is equal to ( n- 1)! or "( n -1) factorial."
The application of the principle of enrichment to the solution of the SIC allows you to build an effective technology. In this case, the solution technology consists of two main algorithms. The first algorithm allows to enrich the initial data array, excluding from it those “distances” that cannot participate in the optimal route. The second algorithm allows you to find the best (or close to optimal) route for a traveling salesman.
The problem was posed and solved as the well-known problem of graph theory on finding the optimal Hamiltonian cycle in the graph [42] .
For the optimal Hamiltonian cycle, the following optimality condition holds true: for any simple route that is a part of the optimal Hamiltonian cycle and passes to the top of the graph in the sequence i1, i2, i3, ..., ia, ( a = 4,5, ..., n; il = 1,2, ..., n ) the sum of the weights of the edges included in it ? ( i 1 i 2 i 3 ..., ia ) is minimal compared to any other sum of the form ? ( i1i? 2i? 3 ... i? a-1ia ) :
? ( i 1 i 2 i 3 ... ia ) = min ? ( i1i? 2i? 3 ... i? a-1ia ) (1)
with a = 4, 5, ..., n; i = 1,2, ..., n; i? 2, i? 3, ..., i? a-1,? P.
Here i 2 2, i 3 3, ..., i a a-1 is one of the permutations of the numbers i 2, i 3, ..., ia-1 , P is the set of all permutations of these numbers.
Obviously, if this condition is not satisfied for any values of a and i, then there exists a Hamiltonian cycle with a shorter path length of the vertices i1, i2, i3, ..., ia-1, ia. But, if the resulting Hamiltonian cycle is optimal, then it cannot be improved by changing the bypass path of the vertices i1, i2, i3, ..., ia for any a having values ranging from 4 to n .
The values of a cannot be less than four, since it is obvious that no two Hamiltonian cycles can differ in less than three edges passing four vertices in a consequence of one of two possible workarounds: i1, i2, i3, i4 or i1, i3, i2, i4 .
Let the optimal Hamiltonian cycle traverse the vertices of the graph in the sequence
i 1, i 2, i 3, ..., in, i 1. (1.a)
A Hamiltonian cycle optimal for a certain value of a is called a - optimal. For a = 4, the following inequality holds:
? ( ikik + 1 ) + ? ( ik + 1ik + 2 ) + ? ( ik + 2ik + 3 )?
? ? ( ikik + 2 ) + ? ( ik + 2ik + 1 ) + ? ( ik + 1ik + 3 ).
Condition (2) needs to be checked for all ik = i 1, i 2, ..., in and, if it is true for all ik , then this is a necessary and sufficient condition that the Hamiltonian cycle is 4-optimal. Summing up the left and right sides of the inequalities obtained with the values ik = i 1, i 2, ..., in, we obtain the necessary 4-optimality condition in the form:
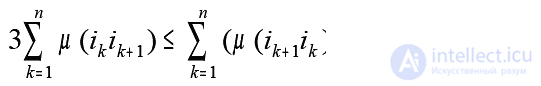
The following condition is true:
If a Hamiltonian cycle is a1- optimal, then it is a2- optimal for any a2 <a1. <Em = "">
If this condition is not met, i.e. If a1 is an optimal Hamiltonian cycle, it is not a2 -optimal, then one of the simple paths of length a1 can be improved by changing the traversal of some a2 vertices, which contradicts the condition of a1 -optimality.
Let us proceed to the definition of the condition a -optimality, obtained in the same way as condition (3) is obtained from (2), from a system of inequalities of the form (2), for any a = const by summation for all ik = 1, 2, ..., n
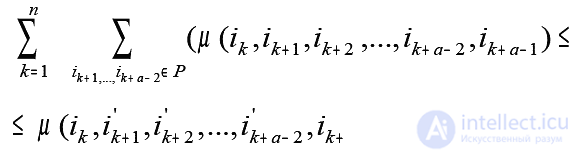
For each value of k, there will be a system of ((a-2)! - 1) inequalities in the number of elements of the set P consisting of ( a-2 ) ! permutations of the numbers i? k + 1 , i? k + 2 , ..., i? k + a-2
At the same time, we believe that
? ( ik, ik + 1 , ..., ik + a-1 ) = ? ( ik, ik + 1 ) + ? ( ik + 1ik + 2 ) + ... + ? ( ik + a-2 ik + a-1 ).
? ( ik, i? k + 1 , ..., i? k + a-2 , ik + a-1 ) = ? ( ik, i? k + 1 ) + ? ( i? k + 1 , i? k + 2 ) + ... + ? ( i? k + a-2 , ik + a-1 ).
Denote the left and right sides of condition (4) by the letters A and B, respectively: A? AT.
In the left part of the inequality, the weight of each edge belonging to the checked part of the Hamiltonian cycle participates exactly once in each inequality of the system of (( a-2 ) ! -1 ) inequalities defined by permutations belonging to the set P , with a fixed initial vertex.
In addition, for a given a = const , if we verify the condition (9.2.4) by changing successively the number of the initial vertex from i1 to in, then any edge of the Hamiltonian cycle will appear exactly in ( a-1 ) systems of these ((a 2 ) ! -1 ) inequalities as the first, second, third, etc. ( a-1 ) -e edge in the checked sections of the Hamiltonian cycle.
Therefore, the left side of inequality (4) has the form:
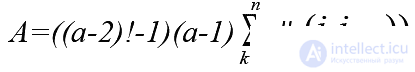
The expression for the right side of condition (4) can be written as:
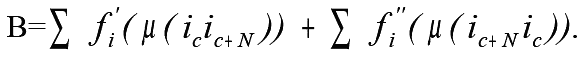
In order to obtain an expression for the right side of condition (4), it is necessary to find the number of occurrences of edges of the graph of the form ( ic, ic + N ) in each system from (( a-1 ) ! -1 ) inequalities given by a certain value of k , and also in all systems of these inequalities, obtained by changing ik from i1 to in .
Obviously, the number of occurrences of pairs ( ic, ic + N ) in the right-hand sides of inequalities of the form (4) is equal to the number of occurrences of pairs ( ic, ic + N ) in the sequences:
ik, i? k + 1 , i? k + 2 , ..., i? k + a-2 , ik + a-1 (5)
asked ( a-2 ) ! permutations of the numbers i? k + 1 , i? k + 2 , ..., i? k + a-2 .
It should also be noted that one of these sequences, namely i1, i2, i3, ..., ik + a-1, is on the left side of these inequalities.
The icic + N pairs can be divided into the following types based on whether they contain “fixed” vertices ik and ik + a-1 :
a) icic + N with c? k; c + n < k + a-1; n > 1, n? a-2; these are pairs of elements in (5) that do not contain elements ik, ik + a-1 and those elements ( i1, i2, i? 2, i3, i? 3, i4 , etc.) that are part of the Hamiltonian cycle ( 1a).
Each of the pairs of this type will appear in the system of inequalities (4) for a particular value ik = i1, i2, ..., in , exactly ( a-3 ) ( a-4 ) ! times - by number ( a-4 ) ! permutations ( a-4 ) elements, i.e. elements of the sequence (5) minus the elements ik, ik + a-1, ic, ic + N for each of ( a-3 ) possible positions of the pair ic, ic + N in the sequence (5).
b) ic, ic + N for n> 1, c = k and ic + Nic + a-1 for n <a-2, c = k are pairs of elements in (5) containing the elements ik or ik + a-1 and elements of the Hamiltonian cycle (1a).
Each of these pairs will appear in the system of inequalities (4) for a particular value ik = i1, i2, ..., in, exactly ( a-3 ) ! times by the number of possible permutations ( a-3 ) elements, since the elements ik, ik + N, ik + a-1 for these pairs are “fixed”.
In addition, in the sets of pairs of both types, it is necessary to distinguish the pairs ic, ic + 1, i.e. pairs of elements of the Hamiltonian cycle (1a). Then we can assume that each of these pairs will appear in the system of inequalities (4) for a particular value ik = i1, i2, ..., in exactly (( a-3 ) ! -1 ) times according to the number of occurrences of pairs of the form a) or b) and minus the occurrences of one pair located on the left side of inequality (4).
Similarly, for any pair of the form IC + N IC, the number of occurrences in the system of inequalities (4) for a certain value of ik is ( a-3 ) ! Here we must take into account the fact that ik and ik + a-1 are “fixed”, i.e. they cannot participate in pairs of the form IC + N IC.
Thus, each pair of elements of the form icic + N that do not form an edge incident to the Hamiltonian cycle, as well as each pair of the type ic + N ic will appear in the right-hand side of the system of inequalities written for a particular value ik , exactly ( a-3 ) ! times, and edges incident to the Hamiltonian cycle, exactly (( a-3 ) ! -1 ) times.
By sequentially setting the values of ik from i1 to in, we get each time new systems of inequalities. In this case, with respect to any edge ic, ic + N, the section ik, ik + 1, ..., ik + a-1 “moves”, as a result of which any pairs ic + N ic or ic, ic + N participate in aN ( k + a-1-n-k + 1 = aN ) systems of inequalities (4). The fact that couples of the form ( ic + N, ic ) with the participation of the elements ik and ik + a-1 in each system of inequalities is impossible, leads to a decrease in the number of occurrences of each such type of pairs ic + N ic in system (4) for a given N into two.
Edges ic ic + 1 thus participate in ( a-1 ) inequality systems, of course , if ( a-3 ) ! -1 ? [1] or a ? 5, i.e., if by the condition they appear at all on the right-hand side of the system of inequalities for any ik.
From here it is obvious that any edge ? ( ikik + N ), N ? 1, the graph will be repeated in the right parts of n systems of inequalities (4) ( a - N ) times for ik = i1 , i2, ..., in .
Consequently, the right side of system (4) takes the form:
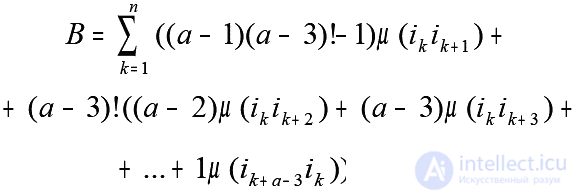
So, the condition of a -optimality takes the form:
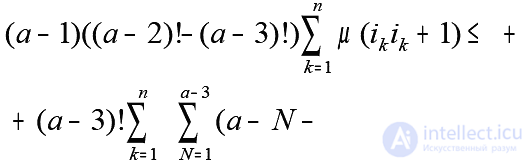
for a ? five.
After simple transformations we get
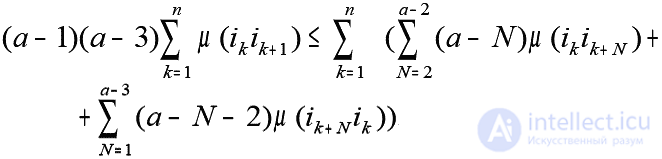
for a ? five.
From here we obtain the n- optimality condition ( a = n )
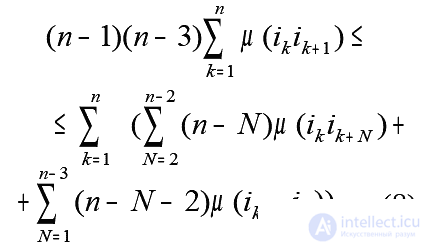
And, further, the condition of ( n +1 ) -optimality ( a = n + 1 ) , i.e. the optimality condition of the proper Hamiltonian cycle takes the form
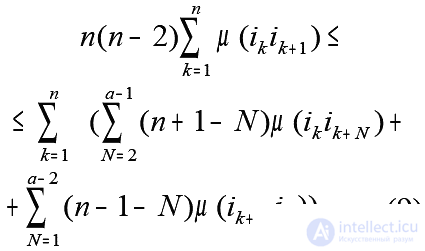
It is possible to strengthen condition (7) by introducing the check for all k instead of checking the total inequality . We obtain the conditions of a- optimality of the Hamiltonian cycle in the form:
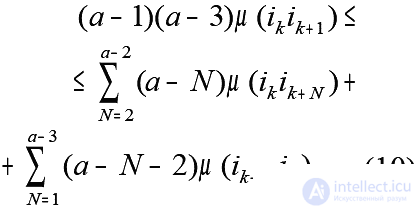
a ? five; k = 1, 2, ..., n.
It was shown above that a1 is the optimal Hamiltonian cycle a2 is optimal if a1> a2 .
Therefore, the optimality condition for a Hamiltonian cycle can be converted to the form ( a = n + 1 ) :
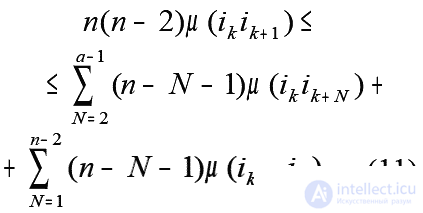
? The “enrichment principle” applied to solving the traveling salesman (OCR) problem is as follows: using a certain condition, check all the branches of the graph for useful properties (in this case, “ability” to participate in the optimal Hamiltonian cycle) and for further solving the problem leave only these "useful" branches. In the case when the condition used is strong enough, after this check only branches of the optimal Hamiltonian cycle will remain. In another case, part of the branches of the graph will be excluded from consideration, which makes it possible to reduce the time for finding a solution using any algorithm.
Thus, the whole process of solving the problem is divided into 2 stages: the first is the “enrichment” of the initial numerical array, the second is the application of the search algorithm on the “enriched” array.
The implementation of the first stage in solving the OLC is performed using the obtained optimality condition for the Hamiltonian cycle in the graph G with n vertices.
The optimality condition can be used to “enrich” the original set of branches of the graph: after checking all the branches of the graph for the optimality condition, the number of branches, which is appropriate to use in further solving OCR, will decrease. Due to the obvious simplicity, the description of the algorithm is not given.
The experience of applying this condition for graphs with n = 11–67 showed that even after a single application of such an operation to all branches of the graph, the number of branches in the enriched array is significantly reduced.
? Systems philosophy can be applied to the formation of holistic theories and practices of the implementation of special scientific knowledge - cultural studies, sociology, and other sciences.
You can use the system philosophy as a methodological basis of special scientific knowledge as follows.
To do this, it is necessary to distinguish three steps to implement this feature:
- the first step: the use of a holistic method, as a philosophy of the whole, to build a holistic philosophy (philosophy of the whole) of specially-scientific knowledge. For example, an integral social philosophy can be built, as a section of social philosophy, an integrated philosophy of culture, as a section of the philosophy of culture.
At this stage, they apply and develop, as applied to the philosophy of this field of knowledge, definitions, as well as postulates and other provisions of the holistic method of system technology. The code of the whole of the given field of specially-scientific knowledge and practice is formed;
- the second stage: the application of the system philosophy method for the construction of a complex of holistic theories of special scientific knowledge, realizing the corresponding holistic philosophy using the models of holistic and whole systems, Principles, rules, Laws of system philosophy.
At this stage, the method of system philosophy can be applied, for example, to build a complex of sociological theories (or cultural theories) that implement an integral social philosophy (or an integral philosophy of culture).
It is quite possible the need to use two or more holistic philosophies of specially-scientific knowledge for the construction of any one theory from the complex of theories of special-scientific knowledge. For example, a holistic philosophy of culture and a holistic social philosophy can be used in building a holistic sociology.
In turn, when building a complex of theories as an integral complex, a certain ordering in this complex is also possible. So, some theories can be identified as key ones, others as hubs, the rest as private ones.
At the same time, by definition, key theories contain models of the formation of nodal and particular theories, nodal - models of the formation of particular theories. On the other hand, key theories allow to solve key problems of a given field of special scientific knowledge, and also contain a holistic basis for solving nodal and particular problems. Nodal theories allow to solve nodal problems of a given area of special scientific knowledge, and also contain a holistic basis for solving particular problems.
Key theories are implementations of the whole code in the key and particular theories of a given field of special scientific knowledge and practice.
Nodal theories are implementations of the code of the whole in the particular theories of a given field of special scientific knowledge and practice.
At this stage, both highly specialized models of this field of knowledge and the same models that are transformed with the help of models of complete and whole systems can be applied. Это могут быть, например, модели социальных, физических, энергетических, биологических, психологических и иных процессов, структур и систем, традиционно применяемые в данной области знания.
– третья ступень: применение метода системной технологии для построения целостных прикладных теорий специально-научного знания и целостных практик их реализации, напр., прикладных социологических теорий, направленных на построение системных технологий социального аудита, экспертизы, анализа, исследований, проектирования, управления и т.д. Или – на построение системных технологий аудита, анализа, экспертизы, исследований, проектирования, управления, мониторинга культуры и ее применения.
В результате, к примеру:
At the first stage, an integral social philosophy will be built, regarding society as a whole and whole. In a holistic and whole society, the core of the whole, the code of the whole, will be identified and described. Objects, subjects and results will be formed as triads aimed at resolving the problems of survival, preservation and development of society as a whole and whole. Holistic social philosophy will also contain definitions and postulates of the holistic method of social philosophy, Principles, rules, Laws, models of the whole and whole activity of the society.
At the second stage, an integral key theory will be built, for example, in a complex of sociological theories. The basic model of the whole and the whole system can then be adopted by the DNIF-model of the whole and the whole system.
На третьей ступени будут построены, напр., прикладные социологические теории, направленные на построение системных технологий социального аудита, экспертизы, анализа, исследований, проектирования, управления и т.д. Будут также разработаны методики формирования и реализации указанных системных технологий практики социальной деятельности.
Такая же последовательность ступеней применения системной философии может быть осуществлена и в отношении культурологии. В результате применения единой парадигмы системной философии к социологии и культурологии все разделы данных наук и соответствующих практик представят собой целостные комплексы знания и практики, легко сопрягаемые друг с другом.
В общем случае, в результате применения единой парадигмы системной философии все разделы определенной науки и практики представят собой целостный комплекс знания и практики, легко сопрягаемый с любыми другими целостными областями специально-научного знания и практики.
Известно мнение Л. Гумилева: "В 18-19 веках благодаря дифференциации наук было накоплено огромное количество сведений, к началу 20 века ставшее необозримым. Образно говоря, могучая река Науки была пущена в ирригационные арыки. Животворная влага оросила широкую территорию, но озеро ранее ею питаемое, т.е. целостное миросозерцание, высохло...", а также, что "узкая специализация полезна лишь как средство накопления знаний: дифференциация дисциплин была этапом, необходимым и неизбежным, который станет губительным, если затянется надолго. Накопление же любых сведений без систематизации их на предмет широкого обобщения – занятие довольно бессмысленное".
Systems philosophy is designed to solve the problem of the complete systematization of knowledge, which is relevant not for the first century, acting in conjunction with those other scientific disciplines, the subject of which is the systematization of knowledge.
Comments
To leave a comment
System analysis (systems philosophy, systems theory)
Terms: System analysis (systems philosophy, systems theory)