Lecture
In this article, we consider the introduction of an ordinal function on an oriented graph. A description will be given of the ordinal function algorithm and its implementation in the C # programming language.
Let's start with the theory. An order function on a directed graph without contours divides the set of vertices of the graph into disjoint subsets, ordered so that if the vertex is in the subset with number i , then the vertex following it is in the subset with number greater than i . The resulting non-intersecting subsets of vertices are called hierarchical levels .
Here is the description of the graph ordering algorithm:
Consider an example. Suppose there is a graph, as in the figure below.
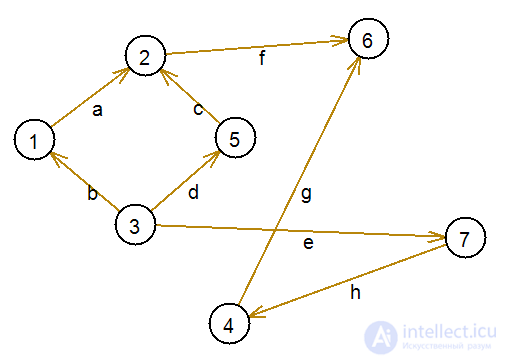
After the introduction of the ordinal function on this graph, we obtain the following:
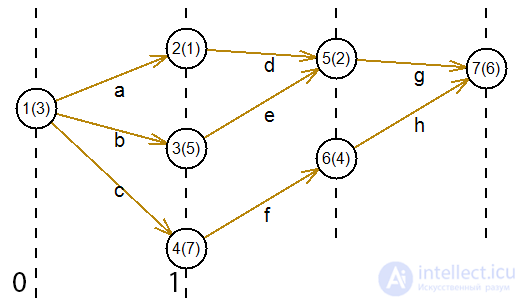
Consider the implementation of the algorithm for introducing an ordinal function on a graph. For development will be used C # language.
Let the arc of a graph be an instance of the Edge class:
public class Edge
{
public int v1, v2;
public Edge(int v1, int v2)
{
this.v1 = v1;
this.v2 = v2;
}
}
where v1 is the number of the vertex from which the arc originates, and v2 is the number of the vertex into which this arc enters.
The hierarchical level of an ordered graph is represented by an instance of the HierarchicalLevel class:
public class HierarchicalLevel
{
public List level;
public HierarchicalLevel()
{
level = new List();
}
}
where level is a list of vertex numbers that are members of this hierarchical level.
The entire set of arcs and hierarchical levels of an ordered graph will be stored in the form of appropriate lists:
List E; List HL = new List()
Let us give an implementation of the createHLevel (...) method, which orders the graph.
public void createHLevel(List HL, int numberV, List E) //numberV - количество вершин
{
List usedV = new List(); //список вершин, уже использованных в порядковой функции
List notUsedV = new List(); //список вершин, еще не использованных в порядковой функции
for (int i = 0; i < numberV; i++)
notUsedV.Add(i);
while (notUsedV.Count > 0)
{
HL.Add(new HierarchicalLevel());
for (int i = 0; i < notUsedV.Count; i++)
{
int k = 0;
for (int j = 0; j < E.Count; j++)
if (E[j].v2 == notUsedV[i])
k++; //считаем полустепень захода вершины
for (int m = 0; m < usedV.Count; m++)
for (int j = 0; j < E.Count; j++)
{
if (E[j].v1 == usedV[m] && E[j].v2 == notUsedV[i])
k--; //вычитаем дуги, иходящие из вершин предыдущих уровней и входящие в вершину i
}
if (k == 0)
{
HL[HL.Count - 1].level.Add(notUsedV[i]);
notUsedV.RemoveAt(i);
i--;
}
}
for (int j = 0; j < HL[HL.Count - 1].level.Count; j++)
{
usedV.Add(HL[HL.Count - 1].level[j]);
}
}
}
The arguments of the createHLevel : HL method are a list of hierarchical levels of a graph, numberV is the number of vertices in a graph, E is a list of arcs in a graph.
We briefly describe the working principle of the createHLevel () method. At the beginning, all vertices are considered unused and are listed in the notUsedV list. The program continues until the notUsedV list is empty. At each iteration for a given hierarchical level, all the vertices from the notUsedV list are searched. For each vertex from this list its half degree of entry (int k) is calculated, then the number of arcs entering the vertex from the vertices of previous levels is subtracted from this number (these vertices are stored in the usedV list). If, as a result, k turns out to be zero, then the vertex belongs to this level: we add its list of level vertices and remove it from the list of unused vertices. At the end of the iteration for this hierarchical level, we update the list of used vertices usedV: we add to it the numbers of the vertices listed in this level.
Note
Since the introduction of an ordinal function is possible only on a graph without contours, it is possible to make an appropriate check of the graph for their presence. To do this, use the algorithm for finding cycles in an undirected graph, slightly modifying it, namely, by removing the backward path along the edge, you will get a function to search for contours in a directed graph.
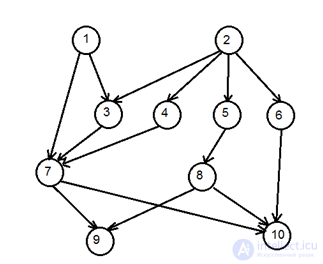
For the structure whose graph is shown in the figure, arrange. Build adjacency matrices to ordering and after drawing up, find out how they differ.
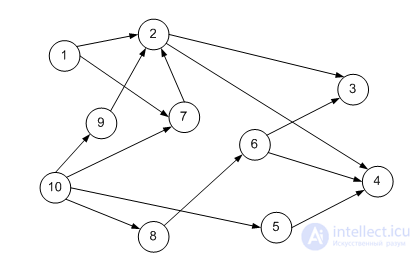
An example solution.
The adjacency matrix of the original graph:

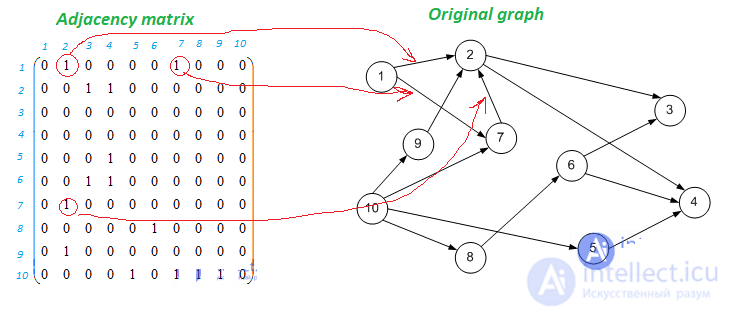
Subsets of vertices:
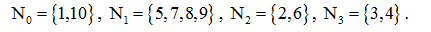
Hierarchical graph obtained from the source:
The adjacency matrix of a hierarchical graph:

public void createHLevel (List HL, int numberV, List E) // numberV - the number of vertices
{
List usedV = new List (); // list of vertices already used in the order function
List notUsedV = new List (); // list of vertices not yet used in the order function
for (int i = 0; i
notUsedV.Add (i);
while (notUsedV.Count> 0)
{
HL.Add (new HierarchicalLevel ());
for (int i = 0; i
{
int k = 0;
for (int j = 0; j
if (E [j] .v2 == notUsedV [i])
k ++; // count the half degree of the peak
for (int m = 0; m
for (int j = 0; j
{
if (E [j] .v1 == usedV [m] && E [j] .v2 == notUsedV [i])
k--; // subtract the arcs coming from the vertices of the previous levels and entering the vertex i
}
if (k == 0)
{
HL [HL.Count - 1] .level.Add (notUsedV [i]);
notUsedV.RemoveAt (i);
i--;
}
}
for (int j = 0; j
{
usedV.Add (HL [HL.Count - 1] .level [j]);
}
}
}
Comments
To leave a comment
System analysis (systems philosophy, systems theory)
Terms: System analysis (systems philosophy, systems theory)