Lecture
| RC6 | |
Feistel network RC6 algorithm |
|
| Creator: |
Ronald Raivest, M. Robshaw, R. Sydney (RSA Laboratories) |
|---|---|
| Created by: |
1998 |
| Published: |
1998 |
| Key size: |
128, 192 or 256 bits (0 to 2040 bits) |
| Block size: |
128 bits (for 32-bit platforms) |
| Number of rounds: |
20 (default) |
| Type of: |
Feistel Network |
RC6 is a symmetric block cryptographic algorithm derived from the RC5 algorithm. It was created by Ron Rivest, Matt Robschaw and Ray Sydney to meet the requirements of the Advanced Encryption Standard Competition (AES). The algorithm was one of the five finalists of the competition, was also presented by NESSIE and CRYPTREC. It is a proprietary (proprietary) algorithm, and patented by RSA Security.
The RC6 cipher variant announced for the AES tender supports 128-bit blocks and 128, 192, and 256-bit keys, but the algorithm itself, like RC5, can be configured to support a wider range of lengths of both blocks and keys (from 0 up to 2040 bits) [1]. RC6 is very similar to RC5 in its structure and is also quite simple to implement.
It is an AES finalist, but one of the primitive operations is a multiplication operation that is slowly performed on some hardware and makes it difficult to implement the cipher on a number of hardware platforms and, which turned out to be a surprise for the authors, on systems with Intel IA-64 architecture is also rather poorly implemented. In this case, the algorithm loses one of its key advantages - high speed of execution, which was the reason for criticism and one of the barriers to being elected as a new standard. However, on systems with a Pentium II, Pentium Pro, Pentium III, PowerPC and ARM processor, the RC6 algorithm is ahead of the winner - Rijndael [2].
Like RC5, RC6 is a fully parameterized family of encryption algorithms. For the specification of the algorithm with specific parameters, the designation is RC6-w / r / b , where
In order to comply with AES requirements, a block cipher must handle 128-bit blocks. Since RC5 is an exceptionally fast block cipher, expanding it to work with 128-bit blocks would result in using two 64-bit working registers. But the architecture and programming languages do not yet support operations, so I had to change the project to use four 32-bit registers instead of two 64-bit ones.
Constant generation:
As in RC5, two pseudo-random variables are generated in RC6 using two mathematical constants: exponent (e) and golden section (f).
{}
,
where Is rounding to the nearest odd integer. When w = 32 bits (in hexadecimal):
Key expansion procedure for RC6-w / r / b:
The key table for the RC6 cipher is also identical to the RC5 cipher table. The difference is that a larger number of words from the array L is obtained from a user-provided key for use during encryption and decryption.
Entrance:
Output:
S [0] = Pw
for i = 1 to 2r + 3 do
S [i] = S [i-1] + Qw
A = B = i = j = 0
v = 3 * max {c, 2r + 4}
for s = 1 to v do
{
A = S [i] = (S [i] + A + B) <<< 3
B = L [j] = (L [j] + A + B) <<< (A + B)
i = (i + 1) mod (2r + 4)
j = (j + 1) mod c
}
RC6 works with four w-bit registers A, B, C and D, which contain input source text and output cipher text at the end of encryption.
Encryption procedure:
Entrance:
Output:
B = B + S [0]
D = D + S [1]
for i = 1 to r do
{
t = (B (2B + 1)) <<< lg w
u = (D (2D + 1)) <<< lg w
A = ((A ⊕ t) <<< u) + S [2i]
C = ((C ⊕ u) <<< t) + S [2i + 1]
(A, B, C, D) = (B, C, D, A)
}
A = A + S [2r + 2]
C = C + S [2r + 3]
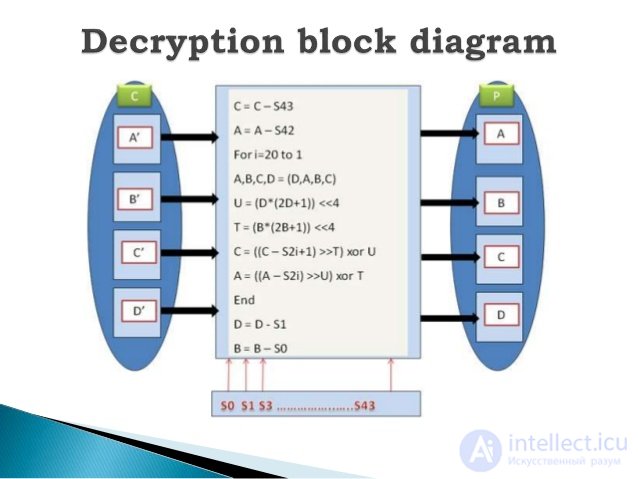
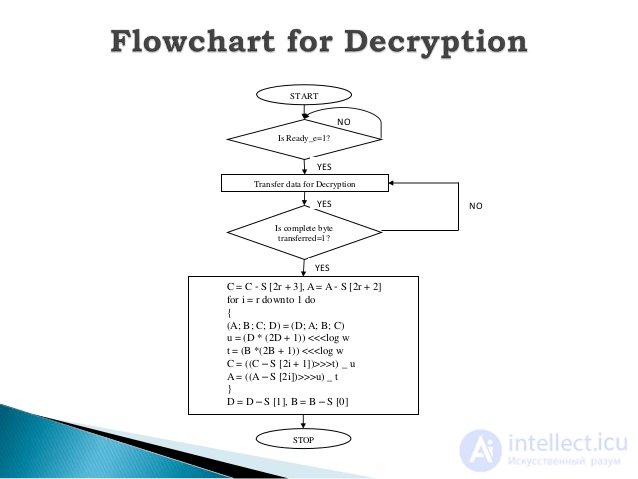
Decryption procedure:
Entrance:
Output:
C = C - S [2r + 3]
A = A - S [2r + 2]
for i = r downto 1 do
{
(A, B, C, D) = (D, A, B, C)
u = (D (2D + 1)) <<< lg w
t = (B (2B + 1)) <<< lg w
C = ((C - S [2i + 1]) >>> t) ⊕ u
A = ((A - S [2i]) >>> u) ⊕ t
}
D = D - S [1]
B = B - S [0]
In this implementation, the word size W = 32 bits is used, which corresponds to a block size of 128 bits. The number of rounds is R = 16. The key K is determined by the user independently. This implementation does not work.
using System;
using System.IO;
using System.Collections.Generic;
namespace RC6
{
class RC6
{
// Constants for swig operations
public const int W = 32;
public const int R = 16;
// Variables for working with files
public Byte [] fileData;
public uint fileLength;
// List of decrypted / decrypted data
public List resultData = new List ();
// Crypto key
public UInt32 [] key = new UInt32 [2 * R + 4];
// The function of writing data to a file
public void WriteByteArrayToFile (Byte [] buffer, string fileName)
{
try
{
FileStream fs = new FileStream (fileName, FileMode.Create, FileAccess.ReadWrite);
BinaryWriter bw = new BinaryWriter (fs);
for (int i = 0; i
bw.Close ();
fs.Close ();
}
catch (Exception ex)
{
// Omitted for implementation under different types of projects
}
}
// Function of reading data from file
public Byte [] ReadByteArrayFromFile (string fileName)
{
Byte [] buffer = null;
try
{
FileStream fs = new FileStream (fileName, FileMode.Open, FileAccess.Read);
BinaryReader br = new BinaryReader (fs);
long numBytes = new FileInfo (fileName) .Length;
buffer = br.ReadBytes ((int) numBytes);
br.Close ();
fs.Close ();
}
catch (Exception ex)
{
// Omitted for implementation under different types of projects
}
return buffer;
}
// right shift function
public UInt32 RightShift (UInt32 z_value, int z_shift)
{
return ((z_value >> z_shift) | (z_value << (W - z_shift)));
}
// left shift function
public UInt32 LeftShift (UInt32 z_value, int z_shift)
{
return ((z_value << z_shift) | (z_value >> (W - z_shift)));
}
// The function of determining the number of shifts
public int OffsetAmount (int dwVar)
{
int nLgw = (int) (Math.Log ((double) W) / Math.Log (2.0));
dwVar = dwVar << (W - nLgw);
dwVar = dwVar >> (W - nLgw);
return dwVar;
}
// Key generation function
public void KeyGen (UInt32 dwKey)
{
UInt32 P32 = 0xB7E15163;
UInt32 Q32 = 0x9E3779B9;
UInt32 i, A, B;
UInt32 dwByteOne, dwByteTwo, dwByteThree, dwByteFour;
dwByteOne = dwKey >> 24;
dwByteTwo = dwKey >> 8;
dwByteTwo = dwByteTwo & 0x0010;
dwByteThree = dwKey << 8;
dwByteThree = dwByteThree & 0x0100;
dwByteFour = dwKey << 24;
dwKey = dwByteOne | dwByteTwo | dwByteThree | dwByteFour;
key [0] = P32;
for (i = 1; i <2 * R + 4; i ++)
key [i] = key [i - 1] + Q32;
i = A = B = 0;
int v = 3 * Math.Max (1, 2 * R + 4);
for (int s = 1; s <= v; s ++)
{
A = key [i] = LeftShift (key [i] + A + B, OffsetAmount (3));
B = dwKey = LeftShift (dwKey + A + B, OffsetAmount ((int) (A + B)));
i = (i + 1)% (2 * R + 4);
}
}
// The function of converting the array UInt32 to the list of bytes
public void ConvertFromUInt32ToByteArray (UInt32 [] array)
{
List results = new List ();
foreach (UInt32 value in array)
{
byte [] converted = BitConverter.GetBytes (value);
results.AddRange (converted);
}
// Formation of a list of encrypted / decrypted data bytes
resultData.AddRange (results);
}
// The function of converting an array of bytes into an array of UInt32 (fitted to the current task)
public UInt32 [] ConvertFromByteArrayToUIn32 (byte [] array, int position)
{
List results = new List ();
// Size of the block of convertible data. We read 16 bytes.
int length = position + 16;
for (int i = position; i
for (int j = 0; j <4; ++ j)
{
if (i + j
results.Add (BitConverter.ToUInt32 (temp, 0));
}
return results.ToArray ();
}
// File decryption function
public void DecodeFile ()
{
UInt32 [] pdwTemp;
for (int i = 0; i
pdwTemp [1] = (pdwTemp [1] + key [0]);
pdwTemp [3] = (pdwTemp [3] + key [1]);
for (int j = 1; j <= R; j ++)
{
UInt32 t = LeftShift ((pdwTemp [1] * (2 * pdwTemp [1] + 1)),
OffsetAmount ((int) (Math.Log ((double) W) / Math.Log (2.0))));
UInt32 u = LeftShift ((pdwTemp [3] * (2 * pdwTemp [3] + 1)),
OffsetAmount ((int) (Math.Log ((double) W) / Math.Log (2.0))));
pdwTemp [0] = (LeftShift (pdwTemp [0] ^ t, OffsetAmount ((int) u)) + key [2 * j]);
pdwTemp [2] = (LeftShift (pdwTemp [2] ^ u, OffsetAmount ((int) t)) + key [2 * j + 1]);
UInt32 temp = pdwTemp [0];
pdwTemp [0] = pdwTemp [1];
pdwTemp [1] = pdwTemp [2];
pdwTemp [2] = pdwTemp [3];
pdwTemp [3] = temp;
}
pdwTemp [0] = (pdwTemp [0] + key [2 * R + 2]);
pdwTemp [2] = (pdwTemp [2] + key [2 * R + 3]);
// Convert to the output array of decrypted data
ConvertFromUInt32ToByteArray (pdwTemp);
}
pdwTemp = null;
}
// file encryption function
public void EncodeFile ()
{
UInt32 [] pdwTemp;
for (int i = 0; i
pdwTemp [0] = (pdwTemp [0] - key [2 * R + 2]);
pdwTemp [2] = (pdwTemp [2] - key [2 * R + 3]);
for (int j = r; j> = 1; j--)
{
UInt32 temp = pdwTemp [3];
pdwTemp [3] = pdwTemp [2];
pdwTemp [2] = pdwTemp [1];
pdwTemp [1] = pdwTemp [0];
pdwTemp [0] = temp;
UInt32 t = LeftShift ((pdwTemp [1] * (2 * pdwTemp [1] + 1)),
OffsetAmount ((int) (Math.Log ((double) W) / Math.Log (2.0))));
UInt32 u = LeftShift ((pdwTemp [3] * (2 * pdwTemp [3] + 1)),
OffsetAmount ((int) (Math.Log ((double) W) / Math.Log (2.0))));
pdwTemp [0] = (RightShift ((pdwTemp [0] - key [2 * j]), OffsetAmount ((int) u))) ^ t;
pdwTemp [2] = (RightShift ((pdwTemp [2] - key [2 * j + 1]), OffsetAmount ((int) t))) ^ u;
}
pdwTemp [1] = (pdwTemp [1] - key [0]);
pdwTemp [3] = (pdwTemp [3] - key [1]);
// Convert Encrypted Data To Output Array
ConvertFromUInt32ToByteArray (pdwTemp);
}
pdwTemp = null;
}
}
}
The variant of the RC6 algorithm, which was declared on AES, as already mentioned, supports blocks of 128 bits in length and keys of 128, 192, and 256 bits in length, and also contains 20 rounds. That is, RC6-128 / 20 / b, where b = 128,192 or 256 bits. In relation to this algorithm, no attacks were detected. Only attacks against simplified versions of the algorithm, that is, an algorithm with a reduced number of rounds, were discovered.
It is believed that the best attack option on the RC6 available to the cryptanalyst is a complete brute-force search of the b-byte encryption key (or the extended key array S [0, ..., 43], when the user-provided encryption key is particularly long). The full search requires operations. Don Coppersmith remarked that due to the significant memory and preliminary calculations, it is possible to organize a “meet-in-the-middle” attack in order to restore the extended key array S [0, ..., 43]. This would require
calculations and thus the required number of operations was equal to
. More advanced attacks, such as differential and linear cryptanalysis, executable on cipher versions with a small number of rounds, are difficult to attack on the full RC6 cipher with 20 rounds. The difficulty is that it is difficult to find good repetitive features or linear approximations with which an attack could be carried out.
An interesting challenge is to set appropriate security targets against these more advanced attacks. To succeed, these attacks typically require large amounts of data, and obtaining {\ displaystyle 2 ^ {a}} blocks of known or selected encrypted / plaintext pairs - a task different from trying to return one key from {\ displaystyle 2 ^ {a}}
possible. It is worth noting that with a cipher operating at a speed of one terabit per second (that is, encrypting data at a speed of {\ displaystyle 10 ^ {12}}
bps), the time required for 50 computers running in parallel to encrypt {\ displaystyle 2 ^ {64}}
data blocks, is over a year; encrypt {\ displaystyle 2 ^ {80}}
data blocks are more than 98,000 years old; and encrypt {\ displaystyle 2 ^ {128}}
data blocks is greater than {\ displaystyle 10 ^ {19}}
years old.
Although data requirements for blocks for a successful attack could be considered as sufficient in practical terms, the developers sought to provide a much greater level of security.
RC5 research did not show weakness in key installation. This led to the use of the same key installation process in RC6. The process of converting a user-provided key to the key table seems to be well modeled by a pseudo-random process. Thus, while there is no proof that no two keys lead to the same key table, this seems very unlikely. This can be estimated as the probability that there are two 256-bit keys, resulting in the same table 44, 32-bit keys, there are approximately {\ displaystyle 2 ^ {2 * 256-44 * 32} = 2 ^ {- 896} = 10 ^ {- 270}} .
We can summarize our safety requirements for RC6 as follows:
- The best attack on RC6 is a complete brute-force encryption key provided by the user.
- Data requirements to organize more complex attacks on RC6, such as differential and linear cryptanalysis, exceed the available data.
An important criterion for the safety reserve is the maximum number of rounds at which an attack is possible. This is possible for 12, 14 and 15 round variants of the RC6.
| Cipher | Number of rounds (b) | Attack type | Text | Memory bytes | Operations |
|---|---|---|---|---|---|
| RC6-128 / 20 / b | 12 | Statistical differences | |||
| 14 | Statistical differences | ||||
| 15 (256) | Statistical differences |
The fourth column “Text” contains information on the number of unencrypted blocks and the corresponding ciphertext blocks corresponding to these keys. The fifth column, "Bytes of memory", contains the maximum number of bytes of memory that are needed at an arbitrary point of attack. The sixth column “Operations” indicates the expected number of operations that must be performed to launch an attack.
For most applications, embedding RC6 in software is probably the best choice. The RC6 primitive operations (addition, subtraction, multiplication, excluding or offset) are very well supported by modern microprocessors and therefore it is advantageous to take this into account when developing these processors.
However, in some cases it is useful to have RC6 in the form of an embedded circuit. Then one could reach maximum speed or combine other functions around the RC6. Since RC6 uses the primitive operations described above, it is possible to take advantage of the existing verification when developing circuit modules for implementing these primitive operations. For example, if you implement RC6 using technologies based on matrices of logic elements, this will not bring the desired benefits because of the tremendous efforts that will need to be made to develop a multiplication circuit. The implementation based on this technology is significantly inferior to the implementation based on the processor. But this is not a typical situation and you can easily design a multiplication scheme that will be used as a submodule.
With 20 rounds per block, the encryption time is approximately 100 nanoseconds for each block, providing an estimated data transfer rate of approximately 1.3 Gbit / s.
As follows from the description of the algorithm, the RC6 is very compact. Indeed, the implementation of the RC6 algorithm in Assembler for the Intel Pentium Pro microprocessor can be implemented in less than 256 bytes of code for each of the tasks:
Unlike many other encryption algorithms, the RC6 does not use reference tables during encryption. This means RC6 code and data can be placed in modern cache memory and thereby save memory space.
Given that RC6 is fully parameterized, and that it can be efficiently and compactly implemented, the cipher seems to be especially versatile.
As we have already noted, RC6 provides the user with greater flexibility regarding the size of the encryption key, the number of rounds and the word size of the main computing module.
While RC6, presented for review at AES, is based on the use of 32-bit words (128-bit block size), the future need of the market needs RC6 expansion for other block sizes. The most important are block sizes of 256 bits, which would use the word size of 64 bits and the performance offered by the next generation of system architecture. Also note that the RC6 structure allows exploiting a certain degree of parallelism in the decryption and encryption routines. For example, calculating t and u in each round can be computed in parallel, as are updates A and C. As processors evolve towards increasing the amount of internal parallelism (for example, moving to a superscalar architecture), RC6 implementations must demonstrate greater performance.
Since RC6 was not chosen as AES, there is no guarantee that its use is free. Since January 2007, the webpage of the official RC6 developer RSA Laboratories website contains the following:
"We emphasize that if the RC6 is selected for the AES, we’ll emphasize that if RC6 is selected as AES, then RSA Security will not require any licensing or royalties for products using the algorithm ").
The highlighted word “if” means RSA Security Inc. can now require license and copyright payments for any product that uses the RC6 algorithm. RC6 is a patented encryption algorithm (US Patent 5,724,428 and US Patent 5,835,600).
Block diagram RC6
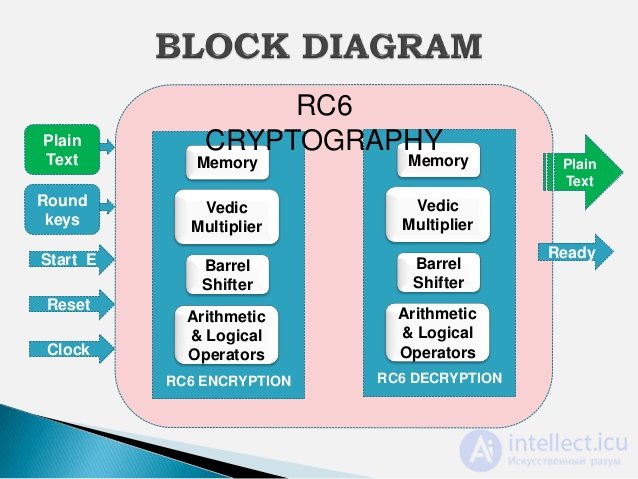
Encryption block diagram
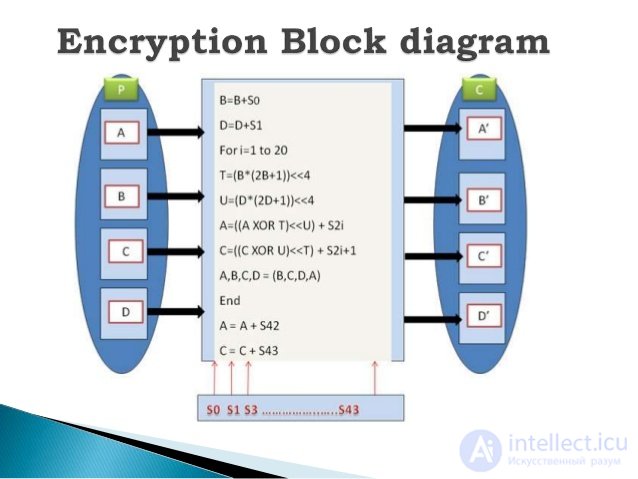
Decryption block diagram
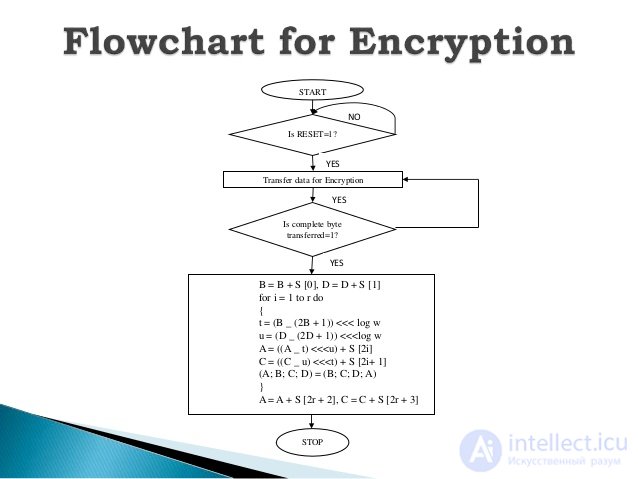
Flowchart for Encryption Блок-схема шифрования RC6 алгоритма
Flowchart for Dencryption Блок-схема дешифрования RC6 алгоритма
Comments
To leave a comment
Information security, Cryptographic ciphers
Terms: Information security, Cryptographic ciphers