Architecture of block ciphers (part 1)

In this issue, we will begin our consideration of the architecture of block ciphers, which unconditionally dominates traditional cryptography at the present stage of its development. From previous releases, we learned that a strong block cipher should have the properties of dispersion and mixing, and that the main idea in building such ciphers is to use a sequence of a large number of simple encryption transformations. Therefore, this issue will begin with consideration of these transformations - the main building blocks of serious ciphers.

By simple encryption transformation, hereinafter, such a transformation is understood, which is implemented by hardware relatively simple logic circuit or software by several computer commands. The following groups of simple ciphers can be distinguished:
permutation cipher - consists in permutations of the structural elements of the encrypted data block - bits, symbols, numbers;
replacement code - consists of replacing one value with another according to the index table, groups of elements of the block being encrypted are replaced - bits or characters;
the cipher of functional transformations is to perform shifts, logical and arithmetic operations on data elements.

Below is a detailed description of each of the mentioned types of transformations:

Permutation ciphers are extremely simply implemented by hardware - wiring conductors on a board or in a chip, without any additional costs at all, since the conductors connecting the equipment registers are somehow present in the circuit. At the same time, these transformations are very inefficiently implemented by software on general-purpose processors. Typically, the computational cost is at least two machine instructions for each binary digit in the modifiable block, unless the permutations are not consistent. This reason, in particular, explains the fact that many ciphers that widely use operations of this type have, all other conditions being equal, significantly less efficient implementations compared to ciphers that do not use them. For example, the American encryption standard DES, a cryptographic algorithm with half the number of steps in the encryption cycle as compared to the Russian standard (16 vs. 32), has approximately twice as slow an optimal implementation for Intel x86 processors.

Common types of replacements are hardware implemented using memory devices, software - indexed reading from RAM, which is essentially the same thing: the replacement for data element x is taken from a vector or replacement node V, which is an array of replacement values, indexed by the replaced data element : x is replaced by

y = v [x].

Programmatically, such an operation is implemented in one command, not counting the operation of loading the index into the appropriate register. The size of the memory required to store the vector of substitutes is determined by the following relationship:

| V | = 2 | X || Y |,

where | x | and | Y | - the sizes of the replaced and replacing blocks in bits, respectively, the size of the vector of replacements V is also obtained in bits. From the above formula it can be seen that it grows exponentially with increasing size of the replaced block. Because of this, it is impossible to perform substitution on the scale of the entire block being encrypted — too much memory would be required to store the vector. Therefore, the transformed data block is divided into fragments, usually of the same size, and they are replaced in these subblocks independently of each other. To improve the strength of the cipher, the replacement of various parts of the block to be encrypted should be performed using different replacement vectors, which together make up a lookup table or a replacement table. The storage of this table requires a memory area of ​​the following size:

| S | = nv | v | = nv2 | X || Y |,

where nv is the number of subblocks of size | X | in which substitutions are made. As noted above, the size of the lookup table quickly increases with the size of the replacement, and especially the replaced block, which entails an increase in the requirements for the memory required for implementing the cipher. On the other hand, the increase in these dimensions complicates cryptanalysis and, thus, increases the cipher strength, therefore, in practice, they should be chosen at the border of reasonableness, because the cryptoalgorithm is designed for a fairly long time, and the capabilities of electronic equipment increase very quickly. In the DES algorithm, the total size of substitution blocks is | SDES | = 8264 = 211bit = 256 bytes. In the domestic standard is the value of the same order: | SGOST | = 8244 = 29bit = 64 bytes. It should be remembered that these ciphers were developed in the seventies, when the concept of "microcircuit" was just beginning to come into our everyday life, the usual storage chip capacity was several dozen, a maximum of hundreds of bits, and the amount of 32K RAM was considered quite a good option for a computer. It is quite natural that the cryptoalgorithms created at that time reflected the harsh realities of those days. Now this problem is practically absent, and therefore modern ciphers are much more free in this respect. Thus, in the BLOWFISH cryptographic algorithm, substitutions are made as follows: each of the 4 bytes constituting a 32-bit word is replaced with a 4-byte word, the resulting words are converted into one using logical and arithmetic operations. Accordingly, the size of one replacement table in this algorithm is | SBLOWFISH | = 42832 = 215bit = 4 KB.

Functional transformations are unary and binary logical and arithmetic operations implemented by hardware-logic circuits, and software by one or two computer commands. Theoretically, it is possible to use any operation that can be formulated in terms of logical functions. However, in practice, the case is always limited to those of them that are available in the instruction sets of the universal processors and are implemented in hardware in the form of microchips. From logical operations these are the basic logical functions - inversion, and binary - bitwise AND, OR, EXCLUSIVE OR, from arithmetic - change of sign (transition to additional code), and binary - addition, subtraction, multiplication, division of some number, from bitwise manipulations - cyclical shifts.

How to build a reliable cipher from elementary operations of the specified type? The most obvious idea is to cascade them, as shown in Figure 1. The symbols P, S, F on it denote permutations (Permutation), replacements (Substitution), and functional transformations (Function), respectively. Key elements (Ki) can be combined with convertible data in substitutions and functional transformations.

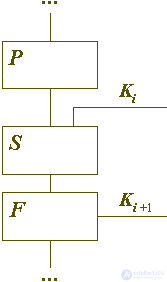
Fig. 1. A fragment of a composite cipher is a combination of a large number of elementary encryption transformations.

It makes no sense to combine two operations of the same type in a row. If we alternate the procedures of different types, the complexity of the resultant transformation (the degree of mixing and dispersion) will be higher. It is very easy to explain: when combining two operations, their complexity is minus a certain “defect of complexity”, which is the more, the more similar the two operations are. For example, the superposition (the result of sequential execution) of two bit permutations can be expressed by one permutation. The same is true for two substitutions performed in the same boundaries of the replaced sub-blocks. Adding to the data block two key elements is equivalent to adding one equal to their sum. In all the cases considered, adding one more to the operation does not at all lead to an increase in the complexity and, therefore, the stability of the transformation.

Even if two different operations belonging to the same group are combined, the complexity of the resulting transformation is less than it could be if they were separated by a different type of operation. Figure 2 shows two three-tier encryption transformations composed of the same operations. The complexity and stability of the transformation depicted on the right, according to the considerations just outlined, is higher than that of the left one.

Fig. 2. A pair of encryption transformations of the three elementary operations used in a different order.

What conditions should the cipher satisfy, not only possessing the necessary strength, but, in addition to this, convenient to implement and use. We will start the consideration with requirements that were particularly relevant a quarter of a century ago, when the capabilities of microelectronic devices were very limited and the considerations of economy and the very possibility of implementing ciphers on the existing element base played a decisive role. Now their relevance is noticeably less, but, nevertheless, they remain sufficiently important to be taken into account in modern developments.
The operation and decryption must be close so that they can be performed by the same hardware or software module - this is dictated by the need for cost-effective implementation.
The volume of key information should be relatively small. A reasonable key size is such that it is impossible to find it by iterating over the entire key space, with a certain margin for the possible progress of electronic equipment. At present, the limit of practical feasibility of key selection is somewhere in the region of 60-64 bits. Accordingly, a key size of 80-256 bits can be considered reasonable. This requirement arises from the need to store keys on any media, including non-traditional ones, for example, on personal miniature magnetic cards.
The implementation of the cipher (program code and fixed data) must be compact enough to fit on microcontrollers with a relatively low storage capacity — the latter requirement is also dictated by considerations of cost effectiveness.

Consider how to build a cipher that meets the specified requirements. Let's start with the condition of reversibility of the encryption procedure. It follows from it that all transformations that directly modify encrypted data should be reversible, that is, when they are executed, information should not be lost. Permutation is reversible by definition. A non-parameterized replacement has an inverse operation if it is surjective, that is, if every possible replacement value occurs in the corresponding replacement vector exactly once. Parameterized, that is, dependent on the value of the key element, the replacement is reversible if, for each fixed parameter value, the corresponding simple replacement is reversible. A binary functional operation is reversible if for each fixed value of the second modifying argument the mapping given to it is surjective, this is equivalent to the condition that the modification equation of the data element Y = f (X, K) is always uniquely solvable with respect to the modified element (X). Unary functional operations can be considered as some binary ones with a fixed second operand. From simple reversible unary and binary logical operations on numbers of finite capacity, one should note the inversion and bitwise exclusive operation or, from arithmetic, changing the sign of a number, addition or subtraction of numbers, multiplication and modulo prime numbers within the discharge grid. If an encryption transformation is defined as a chain of elementary operations described above, it is sufficient to simply construct the inverse of it, if only all elementary operations in the chain are reversible.

To do this, it is enough to fulfill the requirements listed below, which, although they are not absolutely necessary, nevertheless exhaust practically all cases of effectively implemented transformations, and therefore are always taken into account in practice:
All encryption transformations must accept as input and output a data block of the same size, not counting the additional inputs for the replacement parameter and the second operand of the functional transformation.
The substitutions applied directly to the encrypted data must be reversible, the parameterized substitutions must be reversible for each fixed value of the parameter.
The equation of functional transformation of encrypted data using a binary operation must always be uniquely solvable with respect to the transformed (first) operand.

In this case, for a composite encryption transform having a linear structure, you can obviously construct an inverse transform: it is constructed by combining the references of its constituent parts in the reverse order to the one in which they were used in the original transform, as shown in Figure 3.

If the direct transformation is determined by the formula

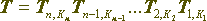
then the inverse transformation is given by the following formula:

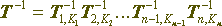
In these formulas denotes one of the simple transformation operations listed above (permutation, substitution, or functional operation), possibly depending on the parameter - the key element Ki. Operations are grouped from right to left, that is, (T2T1) (X) denotes T2 (T1 (X)).

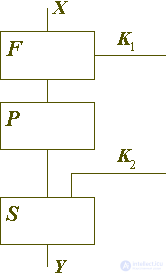
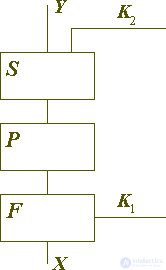
Fig. 3. Encryption transformation with linear structure and inverse encryption transformation.

In order for direct and inverse transformations to be possible to be implemented in a single hardware unit or software module, they must be identical to the accuracy of the key elements used. This means that the encryption transformation must be “antisymmetric” to itself — for each step it takes, which is located at a certain distance from the start of the transformation, the opposite step should be located at the same distance from its end, using the same key element:

T-1 ~ T,

if the following condition is true for all i:

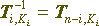for all Ki, or Ti-1 == Tn-i.

If this condition is fulfilled, the procedure for decoding and decryption can be carried out by the same software and hardware module and differ only in the order in which the key elements are used.

Now consider the requirement of a relatively small key size - as noted above, it should not be much larger than the size to exclude the practical possibility of finding it by brute force over the entire key space. Since this "critical" size is currently about eight bytes, a reasonable key size does not exceed 256 bits. It is clear that in order to obtain the necessary cipher strength, it is necessary to use a sufficiently large number of elementary transformation steps that need a set of key elements, much (at times) exceeding the key size. Therefore, in all ciphers of this type, the "deployment" procedure is used, with the help of which an array of key elements of the required size is constructed from a small key.

The key "deployment" procedure should meet the following requirements:
Bits (symbols) of each key element must be equally probable and statistically independent from each other.
The bits (characters) of each key element must be statistically independent of the bits (characters) of several neighboring key elements. This condition must be fulfilled within such a number of encryption steps, on which it is still possible to trace the statistical dependencies between the bits (characters) of the encrypted blocks.

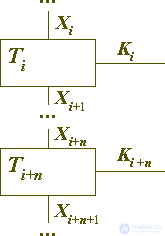
Fig. 4. Steps encryption transform.

This requirement is illustrated in Figure 4. For any pair of steps for encrypting education, not necessarily contiguous, the smaller the correlation of the key elements used by them is allowed, the greater the correlation of the output of the first one with the input of the second:

| C (Xi + 1, Xi + n) || C (Ki, Ki + n) |

where C is a measure of correlation. It is clear that this dependence is not quantitatively strict, it reflects the essence of the issue only qualitatively. Again, it should be noted that this requirement is not absolutely necessary. There is nothing terrible if it is not fully implemented for individual pairs of transformation steps. However, systematically ignoring this rule leads to the fact that the cryptanalysis of the cipher is greatly facilitated.

The cryptoresistance of a sequence of key elements is optional, but a very useful feature of it, since it in itself guarantees that the two requirements above are met. Возможны различные подходы к выработке ключевых элементов для шагов шифрования - от самых простых, до обладающих сложностью, сопоставимой со сложностью самого шифра. Например, в качестве ключевых элементов для шагов шифрования можно просто брать фрагменты ключа, как это делается в отечественном стандарте шифрования. Можно вырабатывать ключевые элементы с помощью генератора псевдослучайных чисел. Здесь спектр возможных решений чрезвычайно широк - от сравнительно несложных схем выработки гаммы на основе сдвиговых регистров с обратной связью до генерации последовательности элементов с помощью того же самого криптоалгоритма. Последний подход реализован, например, в шифре BLOWFISH. Конечно, он значительно увеличивает стойкость шифра, но и существенно затрудняет его эффективную реализацию. Например, в упомянутом шифре BLOWFISH построение массива ключевых элементов вычислительно эквивалентно выполнению более 500 циклов шифрования, что делает его непригодным для реального практического использования всюду за исключением систем, в которых смена ключа происходит достаточно редко, и объемы массивов, шифруемых на одном ключе, велики.

Наконец, требование компактности реализации алгоритма с точки зрения кода и используемых постоянных данных приводит к идеологии его построения из одинаковых групп преобразований, повторенных нужное число раз. В этом случае реализация алгоритма работает итеративно - результат каждой итерации, за исключением последней, является входом для следующей итерации. Кроме того, очевидно, что каждая повторяющаяся группа преобразований, из которых построен криптоалгоритм, должна удовлетворять рассмотренному выше требованию антисимметричности прямого и обратного криптопреобразований, которое в данном случае должно выполняться на уровне отдельных групп.

Требование компактности вспомогательных массивов данных можно выполнить, используя на разных итерациях преобразования один и тот же комплекта векторов замен.

Таким образом, в настоящем выпуске мы с вами рассмотрели базовые требования, в соответствии с которыми строятся современные шифры:
построение шифров из простых преобразований - перестановок, подстановок, элементарных функциональных операций и чередование операций различного типа;
циклическая, итеративная структура алгоритма - одна итерация состоит из нескольких простых преобразований, итерации отличаются друг от друга только использованными ключевыми элементами;
антисимметричная структура алгоритма, позволяющая достичь структурной эквивалентности процедур за- и расшифрования, они отличаются друг от друга только последовательностью использования ключевых элементов;
the use of a key of relatively small size and the development of an array of key elements from it for the transformation steps using the key “unfolding” procedure.