Architecture block ciphers. Part 3

The two previous issues were devoted to the architecture, which is the de facto standard in the construction of modern symmetric ciphers. In this issue, we end this issue.

So that the gamma block developed and used on the encryption round can take on any possible value — this is necessary to ensure high cipher strength — the total size of the encryption part of the block and the round key should not be less than the size of the encrypted part of the block:

| Ki | + | Li | | Hi |.

Moreover, to complicate the analysis of the algorithm, it is advisable to choose these dimensions so that each of them individually is not less than the size of the encrypted part of the block:

| Ki |, | Li | | Hi |.

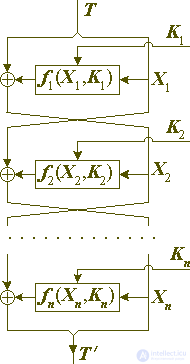
For this reason, in practice, Feistel ciphers are not so common, in which the encrypting part of the block is smaller than the size | Li | <| Hi |, especially for block sizes not exceeding 64 bits. On the other hand, in one round, | Hi | block bits, and if this value is reduced, then with a fixed number of rounds, each block bit will be encrypted fewer times, therefore Feistel ciphers with the size of the encrypted part of the block less than the encryption, also did not receive significant distribution. Thus, ciphers remain in which the dimensions of both parts of the block are the same: | Li | = | Hi |. It is these ciphers, whose architecture, as noted above, is called the Feistel balanced network that dominate modern practical cryptography. They can be represented schematically in two ways, as shown in the left and right sides of the following figure 1. The right scheme defines exactly the same transformation as the left one and is made under the assumption that the number of rounds (n) is even.

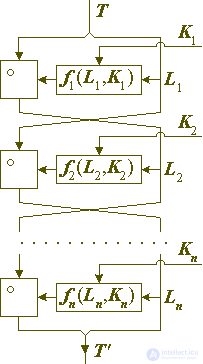
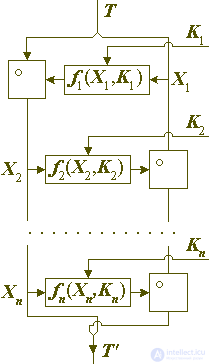
Fig. 1. Balanced generalized Feistel network.


In the Feistel balanced network, conversions are performed according to the following equations:

X0 = Hi | T | / 2 (T), X1 = Lo | T | / 2 (T),
Xi + 1 = Xi-1 of (Xi, Ki), for i = 1,2, ..., n,
T '= Xn + 1 || Xn,

where n is the number of rounds in the encryption procedure.

In a well-rounded Phystel cipher, half the data block is encrypted for one round, so that both parts of the block are encrypted the same number of times, the number of rounds is even.

If, in encryption rounds, to apply a bitwise exclusive OR operation to overlay a gamut, it is very easy to show by induction on the number of rounds that the decoding and decryption procedures differ from each other only in the order of using the key elements and functions of the encryption of the round, as shown in the following figure 2 :

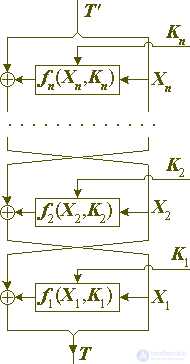
If the sequence of round functions used in the cipher is palindromial (i.e., if 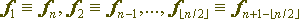), and, in particular, if the same encryption function is used on all rounds, then the decryption and decryption procedures differ only in the order in which the round keys are used - they are mutually inverse. In this case, the cipher has a very useful from the point of view of ease of implementation property - the recording and decryption procedures can be performed by the same hardware or software module. Using the same or almost identical encryption functions will allow to achieve another very desirable property of the cipher - iteration. This means that all the iterations-rounds can be performed by the same module, as a result of which it will be possible to obtain more compact cipher implementations.

It should be noted that in the chain of block transformations in ciphers of a similar structure, sometimes the transformations considered in release 4 — the so-called direct transformations — permutations, substitutions, and functional operations directly on the data being encrypted are added. In order for the backing up and decryption algorithms to be structurally equivalent, it is necessary that for each direct transformation included in the algorithm, a few steps from the beginning of the chain, it is symmetrical to it, that is, exactly the same distance from the end of the transformation is the inverse transformation - Accuracy, as described in release 4. Usually, a direct transformation is added to the beginning of the algorithm; this is done in order to “break up” the typical patterns found in the encrypted data. In accordance with the above rule, in this case the inverse transformation is used at the end of the chain. For example, before the first round of encryption in the DES algorithm, a bit permutation is performed, and after the last round, a reverse permutation is performed. Later ciphers use a combination with a key element for this purpose, which is performed much faster than the permutation of bits.

It should be noted that the encryption round is usually called the conversion cycle using the encryption function, which depends on the key of the round and the encryption part of the block in a non-trivial way. If the transformation is simpler, and it uses only the key element or only the encrypting part of the block, such a step, although it could formally be considered as a round, is not considered as such. For example, algorithm steps that implement the simplified transforms shown in the following figure are not considered rounds:

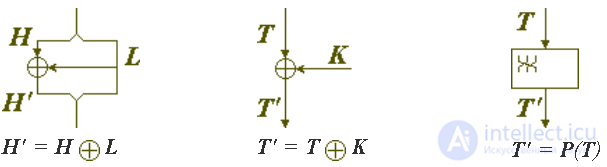
With this we’ll finish reviewing the Feistel networks and move on to considering alternative solutions for building ciphers. Leaving part of the transformed block unchanged is the simplest and most obvious way to obtain an invariant with respect to the transformation, but not the only one. Another way to do this is to divide the encrypted block into several parts and modify them in a consistent manner:

T = (T1, T2, ..., TL),
Ti '= Ti I G,
T '= (T1', T2 ', ..., TL'),

so that some function of the block being transformed does not change its value:

J (T) = J (T '), or J (T1, T2, ..., TL) = J (T1', T2 ', ..., TL'),

where J is an invariant generation function.

A block can be divided into an arbitrary number of parts. However, since usually the block size in bits is a power of two, and it is also desirable to make the dimensions of the parts of the block the same, the number of parts into which it is divided can also be only powers of two. Usually the block to be encrypted is divided into two equal parts:

T = (H, L), | H | = | L | = | R | = | T | / 2 = N / 2.

In this case, to modify the data, pairs of mutually inverse operations can be used, such as addition and subtraction within the discharge grid of blocks, or multiplication and division modulo a simple number. We will not discuss in detail in this release the necessary properties that the operations of this pair should possess; we simply note that they should be similar to the pairs listed above. Suppose, for example, that we use a pair of operations "+", "-" - say, addition and subtraction within the discharge grid of numbers, defined as follows:

H + L = (H + L) mod 2N / 2 and HL = (H - L) mod 2N / 2.

In this case, the procedure for modifying the halves of the block to be encrypted and the function of developing an invariant can be as follows:

H '= H + G, L' = L + G, J (H, L) = HL,
H '= H + G, L' = L-H, J (H, L) = H + L,
H '= H-G, L' = L + G, J (H, L) = H + L,
H '= H-H, L' = L-H, J (H, L) = HL.

In other words, for each pair of operations with the specified properties, four options are possible for using them to perform an encryption step. The common feature of these four variants is that they exhaust all cases in which the subtraction operation (or its analogue from the used pair of operations) is present in the transformation equations an odd number of times, and the addition operation (or its analogue) is even.

It is possible to divide modifiable parts of the block into "zones" in a consistent manner, so that each selected fragment in one part will correspond one-to-one to a fragment of the same size in another part. In this case, for each pair of fragments, you can use your own pair of operations to modify the fragments and develop an invariant:

H = (H1, H2, ..., HK),
L = (L1, L2, ..., LK),
G = (G1, G2, ..., GK),
J = (J1, J2, ..., JK),

where for all k = 1, 2, ..., K holds | Hk | = | Lk | = | Гk | = | Jk | = zk. In this case, the modification of fragments and the development of an invariant is carried out according to the following formulas:

H'k = HkKГk,
L'k = LkKГk,
Jk = Hk K Lk,

where "K" and " K " are a pair of mutually inverse operations on blocks of size zk bits. It is clear that within the framework of applying these two operations to the data fragments, independently of the other fragments, any of the four possible schemes described above can be used. At the same time, however, this division into fragments should not affect the generation of the modifying value (D) from the invariant (J) using the round key element. The nature of the dependence of the second on the first must fully comply with the principles of mixing and dispersion - all bits of G must depend on all bits of J, and the nature of this dependence must be as complex and confusing as possible.

As always, a special case arises when using the bitwise exclusive OR operation, since it is inverse to itself. In this case, instead of four possible combinations of use, we get only one:

H '= H + T, L' = L + T, J (H, L) = H + L.

Such an invariant is used in the well-known IDEA cipher. The round of the standard architecture cipher, when used to obtain an invariant of the bitwise exclusive OR operation, looks as shown in Figure 4 below:

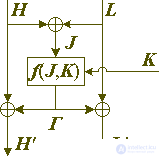
Fig. 4. A method of constructing a round of encryption in encryption networks of a general type using an exclusive OR operation.

It is obvious that adjacent cipher rounds should use different invariants or should be separated from each other by an additional transformation of a different type than that used in the round for modifying the block. Otherwise, we would get about the same result as if there were no permutations of the higher and lower parts of the block between the rounds of the Feistel cipher. If several adjacent rounds use the same invariant, then it will be an invariant of this whole chain of rounds. This almost trivial statement is very easily proved by induction on the number of rounds. It is clear that ignoring this feature of encryption systems can greatly reduce the strength of a cipher. To avoid this between rounds of the type described above, it is necessary to include direct transformations of the block to be encrypted, or its modification using key elements, or rounds with a different invariant and with another operation used to modify the block on the round.

In other words, invariants of adjacent rounds in a common encryption network should resemble each other as little as possible. If between them the value of the parts of a block is modified using key elements, the operation used for this should be as different as possible from the operation of combining data with the modifying block in a round. Even for different operations of the same additive group, the differences may not be enough to obtain the desired durability. A good solution in this situation is the use of operations of a different type, for example, multiplicative ones. This approach is implemented in the IDEA cipher already mentioned above. It is clear that the use of the multiplication operation can greatly reduce the efficiency of the implementation of the algorithm, especially on relatively simple microprocessors, microcontrollers and single-chip computers. That is why this type of cipher is more exotic than common, there is only one widely known and used representative of this class of ciphers - IDEA.

As an alternative to using multiplicative operations for inter-round modifications of the block to be encrypted, it is possible to suggest combining with a key element using a simpler operation of the additive group and then performing substitutions.

The cipher of the considered architecture has the structure shown in Figure 5.

This concludes the discussion of this topic, in conclusion we summarize all three recent issues:
All modern reliable ciphers are composite, that is, they are built from a large number of relatively simple encryption transformations so as to fully ensure the presence of mixing and dispersion properties.
As the "building blocks" ciphers used bit permutations, replacement (substitution) in the bit groups, arithmetic and logical operations. In this case, the greatest mixing and dispersion of the cascade of encryption transformations is achieved if adjacent operations in the chain differ as much as possible from each other.
To complicate ciphers and increase their durability, they are usually built on the basis of encryption structures in which data is converted in one step (round) of encryption, leaving the value of a certain function of the block to be encrypted invariant, and the encryption itself consists in generating a block of code from the round invariant and the key element round using the encryption function, and modifying it using an encrypted data block. Such encryption structures are sometimes called encryption networks.
If two adjacent encryption rounds have the same invariant or if binary operations of the same group are used to modify data on two adjacent rounds, then between them it is necessary to perform a direct modification of the encrypted data block using the operation that destroys this invariant for the specified pair of rounds.
The simplest and most popular way to create an invariant is to leave part of the block to be encrypted unchanged. In this case, for the interraund modification of the block to be encrypted, a cyclic shift is used, which degenerates in exchange for its higher and lower half, if their sizes are the same. Encryption structures built on this principle are called Feistel networks.
Another sometimes used method of obtaining an invariant is to modify the halves of the block being encrypted in a consistent manner using a pair of mutually inverse additive binary operations. In this case, between rounds of encryption, it is advisable to modify the block to be encrypted using other types of operations, for example, multiplicative ones.
The use of encryption on rounds usually requires more key information than is contained in the encryption key. To generate the necessary amount of key information for its subsequent use in rounds, various schemes are used, from the simplest — reusing the same key fragments as in GOST, to the most complex — generating key elements using the same encryption transformations that are used when encrypting, as in the BLOWFISH cipher.