Lecture
In the previous release, we looked at the general principles for constructing block ciphers and found out that they are built from elementary encryption transformations, which usually take the form of bit group replacements, bit swaps, and logical and arithmetic operations. We also learned some of the rules for grouping various operations that increase the robustness of the final cryptographic transformation. In this issue, we will continue to look at the block cipher architecture that dominates today's cryptography.
By combining simple encryption transformations into a linear chain, you can create a completely reliable composite cipher. However, to achieve an acceptable durability of such a cipher, it would be necessary to use a very large number of elementary transformations. This scheme for constructing cryptographic algorithms did not receive any noticeable spread, because another scheme was proposed that has the best conversion complexity / complexity parameters. Higher efficiency is achieved in it using the following general principle:
If there is a data processing system composed of relatively simple transformation blocks, then, in general, its complexity is much higher if the structure of this system is non-linear and contains branches and loops.
Recall that the algorithm with a highly branched structure is much more difficult to understand than the linear algorithm. Another example, from the theory of automatic regulation: analog signal conversion systems containing feedback loops and parallel branches are an order of magnitude more difficult to analyze than circuits composed of the same dynamic links, but having a linear structure. Thus, it is possible to complicate the ciphering transformation with a fixed number of elementary steps if its structure is made nonlinear. Both the present and the next issues will be devoted to discussing how to achieve this goal in practice.
Before proceeding directly to the consideration of the subject of this issue, let us return to the topic of the previous issue, and consider one question that remained in it without the necessary lighting. Recall that key data can be combined with encrypted data in two types of transformations: replacements and functional operations. It turns out that the second way to use key information is preferable. Instead of sharing the inputs of the replacement vector between the block of encrypted data and the key element, it turned out to be more advantageous to combine the data with the key by means of a suitable binary operation, and then subject the result to the replacement. Suppose, for example, that we convert a 32-bit data block using a 32-bit key and several replacement nodes with a 4-bit input. If we use replacement nodes for combining the key and data, then we will need to use 16 replacement nodes of 4 bits for 2 bits, two bits of encrypted data and two bits of the key will be fed to the input of each replacement node. Moreover, each output bit of such a node will depend on exactly two data bits and two key bits. If we convert the replacement to a bitwise modulo 2 data key, we will need to use 8 4-bit 4-bit replacement nodes, and each output bit of the replacement node will depend on four key bits and four data bits. Thus, in this transformation, a greater degree of mixing and dispersion can be achieved.
As a result of the above, practical binary codes for combining encrypted data and a key almost universally use binary operations of additive and, much less often, multiplicative type. Consider this procedure, the corresponding conversion unit is shown in Figure 1:
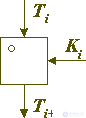
Fig. 1. Combining the key element with the data using the binary operation "o".
In this case, the conversion is carried out according to the following equation:
Ti + 1 = Ti o Ki.
The binary operation "o" used to modify the encrypted block must have the property necessary for the gamma overlay operation, in particular, there must be an inverse operation 0 such that for any T and K data blocks of admissible size the following condition must be met:
(T o K) 0 K = T.
The complexity of the transformation will significantly increase if the key code is not directly combined with the data, but the code generated from the key and dependent on the data, as shown in Figure 2:
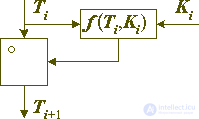
Fig. 2. Encryption transformation of a data block using code derived from the key element Ki and the encrypted Ti block.
In this case, the conversion is carried out according to the following equation:
Ti + 1 = Ti o f (Ti, Ki).
In fact, it is clear that from a mathematical point of view, this record differs little from the most general form of the transformation record: Ti + 1 = F (Ti, Ki), (*)
however, unlike the latter, it contains some indications of a possible way of its implementation. Its important feature is that reversibility is no longer required of the transformation function f from the first equation, as is the function F of equation (*), it only requires as much complexity as possible plus the fulfillment of some additional conditions that can be greatly simplified be formulated as the absence of loss of information in its calculation. The fact is that when creating an encryption transformation of a general form, it is necessary to reconcile two contradictory requirements:
the transformation must be reversible - otherwise decryption will be impossible;
the transformation must be quite complex and non-linear - otherwise it cannot claim to be a truly encrypting transformation.
It is clear why these requirements contradict each other — performing the inverse transformation is nothing more than solving a direct transformation equation with respect to one of its arguments, however, if this equation is non-linear, then there are no general methods for solving it.
The reversibility of the transformation depicted in Figure 2 means that there must exist an effectively computable function g (Ti + 1, Ki), which has the following property:
f (Ti, Ki) = g (Ti + 1, Ki) = g (Ti o f (Ti, Ki), Ki) (**)
for any valid data blocks Ti and Ki. In this case, the inverse transformation will have the form shown in Figure 3:
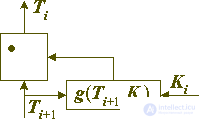
Fig. 3. Inverting the encryption transform.
The inverse transform is performed in accordance with the following equation:
Ti = Ti + 1 0 g (Ti + 1, Ki).
In the general case, it is rather difficult to construct a pair of transformation functions (f and g) that satisfy equation (**) and are complex and nonlinear. However, this is possible if we separate the requirement for the complexity of the functions f and g from the requirement for the condition (**). This can be easily done if the modification operation of the encrypted block is used, which leaves unchanged the value of some function from the transformed data block:
Ii = J (Ti) = J (Ti o Gi) = J (Ti + 1)
for any data blocks Ti, Gi appropriate size. It is clear that in this case the inverse operation "" also has the specified property:
Ii = J (Ti + 1) = J (Ti + 1 0 Гi) = J (Ti).
In the case of constructing an encryption transformation according to the indicated principle, the direct and inverse transformation will have the structure shown in Figure 4 below:
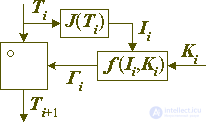
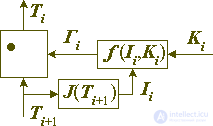
Fig. 4. Standard encryption transformations: direct (left) and reverse (right)
For definiteness, we will call this transformation the standard encryption transformation or the standard encryption step, and the cipher architecture that they specify is the standard or basic cipher architecture. Their use makes it possible to separate the very difficult task in the general case of creating a transformation that has both high complexity and non-linearity on the one hand, and which is reversible on the other, into two subtasks that can be solved independently of each other:
creating a data conversion function with high complexity and non-linearity;
creating a transformation scheme using the given transformation function and at the same time reversible regardless of the function used.
The function J (Ti) used to separate the data block that is invariant with respect to the transformation from both the block itself and the result of its conversion is called the standard encryption transformation invariant or the standard encryption step invariant, and the function f (Ii, Ki) designed to generate the data block used to modify the block to be encrypted from the invariant Ii and the key element Ki is called the encryption function of the transformation step. The encryption step itself in ciphers constructed in accordance with the stated principles is called an encryption round or simply a round.
In this case, the direct and inverse encryption transformations are carried out in accordance with the following equations:
Ti + 1 = Ti of (J (Ti), Ki),
Ti = Ti + 1 0 f (J (Ti + 1), Ki).
Before proceeding with the consideration of the necessary properties of standard encryption transformations, let us discuss the possible relationships between the sizes of the blocks participating in them. If between the sizes of the block being converted (Ti), the modifying value (Гi) and the invariant (Ii), the following relation | Ti | = | Gi | + | Ii |, (***)
then the data modification operation ("") should not lose information about its arguments - this, in particular, means that changing any of the arguments should lead to a change in the value of the function. If equality (***) is not fulfilled and its left side is larger than the right side, then the transformation resistance will be far from the optimum — it can be improved by increasing the size of the modifier (Гi), invariant (Ii), or both. If the right-hand side turns out to be larger than the left-hand side, then the modification operation will necessarily lose information about the modifying element - this means that there will be various elements of G and G ', such that the following equality holds for some data block T:
T o G = T o G ',
in which there is also little point. Thus, it is reasonable to choose the sizes of the blocks participating in the transformation, such that the equality (***) given above is fulfilled. We go further, in terms of achieving the necessary durability and efficiency of the encryption transformation, it is advantageous to take the sizes of the modifier (Gi) and the invariant (Ii) equal: | Gi | = | Ii |. Given the equality (***), their size will be equal to half the size of the block being encrypted:
| R | = | I | = | T | / 2.
This relationship is performed for the vast majority of modern practical ciphers, built in accordance with the described architecture.
Let us continue the consideration of the standard cipher architecture: the invariant and the encryption function can be different for different encryption steps. Let us recall the desirable property of cryptoalgorithms discussed in the previous release — the possibility of implementing direct and inverse transformations with the same hardware unit or software module. For ciphers that have the architecture in question, this is possible if they have an antisymmetric structure. This means that the modification operations used in the steps equidistant from the beginning and the end of the transformation chain must be inverse to each other, and their invariants and encryption functions must be the same:
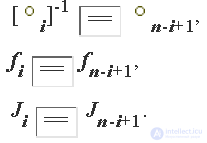
In the simplest way, this can be achieved if the modification uses the bitwise exclusive OR operation, changing the whole block or its part, and taking all the invariants and encryption functions to be the same.
Now let's talk about how you can create an invariant in the encryption transform. One of the most obvious ways to do this is ... not to change a certain part of the block being transformed, to leave it unchanged, literally invariant, as shown below in Figure 5. In this case this unchangeable part of the block will be an invariant For definiteness, suppose that this is the younger part.
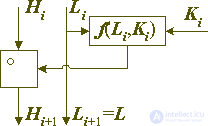
Fig. 5. Standard encryption transformation of a data block, in which the invariant is a part of an encrypted block.
In this case, the conversion is carried out according to the following equations:
Hi + 1 = Hi o f (Li, Ki),
Li + 1 = Li,
where Hi and Li are the high and low parts of the data block being converted, respectively. That part of the block that does not change on the round, let's call the encrypting part, and the part that undergoes the transformation - the encrypted part. Since one of the parts of the block during such a transformation is not subject to change, it is clear that in order to build a strong cipher, before each new conversion step it is necessary to divide the block in a new way into encrypting and encrypting parts. It is intuitively clear that in order to ensure maximum durability, all other things being equal, it is necessary to ensure that all binary digits of the block enter the encrypted part the same or almost the same number of times. Technically, this can be achieved in various ways, for example, after each conversion step, perform a cyclic block shift, which leads to block positions that do not change in the previous step to the encrypted (senior) position. Or alternate the transformation steps, as shown in Figure 6 — on the odd steps, modify the older part of the block using the younger one, and on the even steps — on the contrary, the younger part using the older one.
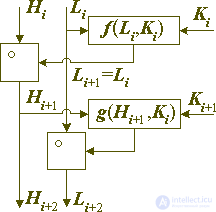
Fig. 6. A pair of complementary encryption transformations.
The conversion is carried out according to the following equations:
Hi + 2 = Hi + 1 = Hi o f (Li, Ki),
Li + 2 = Li + 1 o g (Hi + 1, Ki + 1) = Li o g (Hi + 1, Ki + 1),
The cipher architecture based on the transformation described above, which leaves a part of the block being encrypted unchanged, is called a Feistel network, or more precisely, a generalized Feistel network. The difference between them lies in the fact that in the first one, the bitwise exclusive OR operation is used to modify the data, and the second is any suitable binary operation. This cipher architecture was proposed in the 70s by a pioneer in creating cryptographic algorithms of this type by Dr. Horst Feistel, who at that time worked in the IBM research laboratory and created the Lucifer cryptosystem there, which served as the prototype for the American encryption standard, the DES cryptoalgorithm preserving its status as a standard up to the present, but, obviously, the last few months living in this capacity.
In general, the two parts into which the data block to be converted is divided may be of unequal size. You can always imagine a cipher of this type in such a way that the younger part of the block is encrypted, and the older part is encrypted. In this case, between rounds, it is necessary to perform the rotation of the block in any direction so that the next round is the part of the block that was included in the previous part of the encryption part. It is clear that for each round the division of the block into the encrypting and encrypting parts will be performed anew.
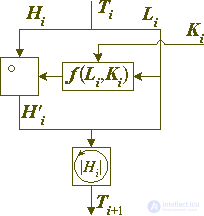
Fig. 7. Round of encryption in the generalized Feistel cipher.
If you represent a convertible data block as an unsigned integer, then the conversion equation for one round will be as follows:
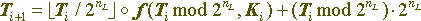
if it is interpreted as an array of bits, the equation will be as follows:
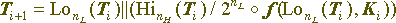
where Lon (X) and Hin (X) denote a block of n, respectively, the low and high bits of the block X, X || Y is the concatenation of blocks X and Y, their combination into one data block in such a way that X is the highest part of the combined block, and Y is its lowest part, through X the integer part of the real number x, nH and nL is the size of the highest number ( encrypted) and younger (encrypting) parts of the converted block.
Of course, the size of the encryption and encrypted part of the block may vary from round to round, but this does not make much sense and usually these values are constant for a particular cryptographic algorithm. If they are equal to each other, then such a scheme is called a balanced one, and if not, then an unbalanced Feistel network.
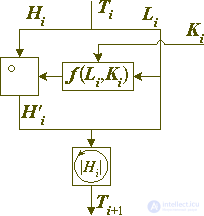
Fig. 7. Round of encryption in the generalized Feistel cipher.
If you represent a convertible data block as an unsigned integer, then the conversion equation for one round will be as follows:
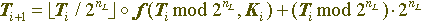
if it is interpreted as an array of bits, the equation will be as follows:
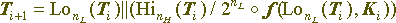
Comments
To leave a comment
Information security, Cryptographic ciphers
Terms: Information security, Cryptographic ciphers