Lecture
With statistically independent signs, the solution of recognition problems is significantly simplified. In particular, when estimating distributions 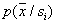 instead of multidimensional probability densities, it suffices to estimate
instead of multidimensional probability densities, it suffices to estimate 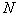 one-dimensional density
one-dimensional density 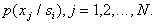
In this regard, the examples of one-dimensional distributions we considered not only are illustrative, but can be directly used in solving practical problems, if there are convincing reasons to consider the signs characterizing objects of recognition as statistically independent. Wherein
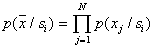
and the Bayes formula used to calculate the posterior probability of an object with attributes 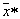 to image
to image 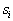 takes the form
takes the form
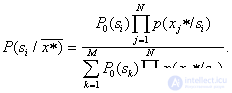
There are practical applications of the theory of recognition, when signs are considered statistically independent without good reason, or even knowing that the signs (at least some of them) are in fact interdependent. This is done to simplify the training and recognition procedures to the detriment of "quality" (likelihood of errors), if this damage can be considered acceptable.
Especially noticeable is the simplification of the Bayesian recognition procedure if the characters take on binary values. In this case, training is to build the following table:
|
|
| ... |
| ||
|
|
|
|
| ... |
|
|
|
|
|
| ... |
|
|
|
|
|
| ... |
|
. . . | . . . | . . . | . . . | . . . | . . . | . . . |
|
|
|
|
| ... |
|
Here 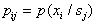 ,
, 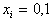 .
.
If a 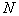 is not very large, then the assignment of an unknown object to a particular image is so simplified that it is often not necessary to use a computer, a calculator is enough, and in extreme cases, it is possible to carry out the calculation manually. It is only necessary to have a pre-prepared table with values.
is not very large, then the assignment of an unknown object to a particular image is so simplified that it is often not necessary to use a computer, a calculator is enough, and in extreme cases, it is possible to carry out the calculation manually. It is only necessary to have a pre-prepared table with values. 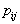 (more precisely, with their estimates). If an unknown object has any signs, then for each of the images in the corresponding row of the table are selected those
(more precisely, with their estimates). If an unknown object has any signs, then for each of the images in the corresponding row of the table are selected those 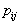 which are associated with these traits, and multiplied. The object belongs to the class, the product for which it turned out to be maximal. In this case, of course, a multiplication by a priori probabilities is carried out, and a posteriori probabilities can be normalized, since it does not affect the result of choosing the maximum by
which are associated with these traits, and multiplied. The object belongs to the class, the product for which it turned out to be maximal. In this case, of course, a multiplication by a priori probabilities is carried out, and a posteriori probabilities can be normalized, since it does not affect the result of choosing the maximum by 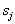 .
.
If the signs are discrete but multivalued, then it is not difficult to proceed to binary values by a special binary encoding.
Comments
To leave a comment
Pattern recognition
Terms: Pattern recognition