Lecture
The likelihood function introduced by Fisher looks like this:
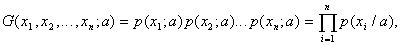
Where 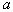 - unknown parameter.
- unknown parameter.
As a parameter estimate  need to choose a value at which
need to choose a value at which  reaches a maximum. Insofar as
reaches a maximum. Insofar as 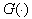 reaches a maximum with the same
reaches a maximum with the same 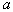 what and
what and 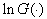 , then search for the required value of the estimate
, then search for the required value of the estimate 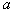 consists in solving the likelihood equation
consists in solving the likelihood equation 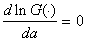 . At the same time all the roots
. At the same time all the roots 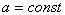 should be discarded, and leave only those that depend on
should be discarded, and leave only those that depend on  .
.
The estimate of the distribution parameter is a random variable that has a mathematical expectation and “scattering” around it. An estimate is said to be effective if its “scattering” around its expectation is minimal.
The following theorem is valid (given without proof). If exists for 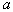 effective evaluation
effective evaluation 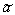 , then the likelihood equation has a unique solution. This decision
, then the likelihood equation has a unique solution. This decision 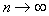 converges to the true value
converges to the true value 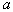 .
.
All this is true for several unknown parameters. For example, for a one-dimensional normal law
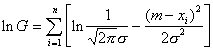 ,
,
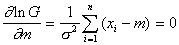 ,
,
from here 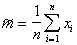 at
at 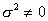 .
.
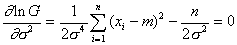 ,
,
from here 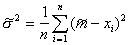 .
.
The estimate is called unbiased if the expectation 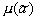 ratings
ratings 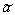 equally
equally 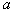 . Evaluation
. Evaluation 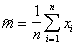 is unbiased. Indeed, since
is unbiased. Indeed, since  - simple random selection from the general population, then
- simple random selection from the general population, then 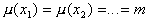 and
and 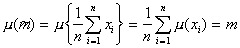 .
.
Find out if 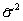 obtained by the maximum likelihood method (or the method of moments), unbiased. Easy to make sure that
obtained by the maximum likelihood method (or the method of moments), unbiased. Easy to make sure that
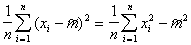 .
.
Consequently,
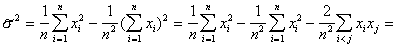
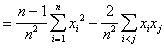 .
.
Find the expected value of this value:
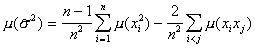 .
.
Since the variance 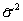 independent of value
independent of value 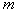 then choose
then choose 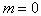 . Then
. Then
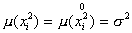 ,
, 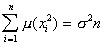 ,
,  ,
,
Where 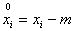 ,
, 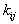 - correlation coefficient between
- correlation coefficient between 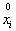 and
and 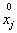 (in this case it is equal to zero, since
(in this case it is equal to zero, since 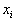 and
and 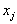 do not depend on each other).
do not depend on each other).
So, 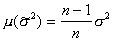 . This shows that the estimate
. This shows that the estimate 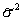 is not unbiased, its expectation is somewhat less than
is not unbiased, its expectation is somewhat less than 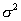 . To eliminate this bias you need to multiply
. To eliminate this bias you need to multiply  on
on 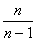 . As a result, we get an unbiased estimate.
. As a result, we get an unbiased estimate.
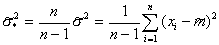 .
.
Comments
To leave a comment
Pattern recognition
Terms: Pattern recognition