Lecture
Parametric estimation of distributions is implemented in cases where the type of distribution is known. 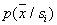 and according to the training sample, it is only necessary to estimate the values of the parameters of these distributions. A priori species knowledge
and according to the training sample, it is only necessary to estimate the values of the parameters of these distributions. A priori species knowledge 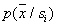 in practice it is not often, however, given the convenience of this approach, sometimes it is assumed, for example, that
in practice it is not often, however, given the convenience of this approach, sometimes it is assumed, for example, that 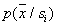 - normal law. Such assumptions are not always convincing, but they are used nonetheless if the learning results lead to acceptable recognition errors.
- normal law. Such assumptions are not always convincing, but they are used nonetheless if the learning results lead to acceptable recognition errors.
So, learning is reduced to estimating the values of parameters. 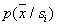 with a previously known form of these distributions. A special place among distributions is occupied by the normal law. This is due to the fact that, as is known from mathematical statistics, if a random variable is generated by the influence of a sufficiently large number of random factors with arbitrary distribution laws and there is no clearly dominant among these influences, then the quantity of interest has a normal distribution law. For one-dimensional case
with a previously known form of these distributions. A special place among distributions is occupied by the normal law. This is due to the fact that, as is known from mathematical statistics, if a random variable is generated by the influence of a sufficiently large number of random factors with arbitrary distribution laws and there is no clearly dominant among these influences, then the quantity of interest has a normal distribution law. For one-dimensional case
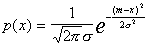
(for simplicity, we will henceforth consider the one-dimensional case, and interested students can refer to the literature cited at the end of the lecture outline).
The parameters of this distribution are two quantities: 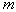 - expected value,
- expected value, 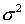 - dispersion. They also need to be evaluated by the sample. One of the most simple is the method of moments. It is applicable for distributions
- dispersion. They also need to be evaluated by the sample. One of the most simple is the method of moments. It is applicable for distributions 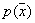 depending on
depending on 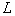 parameters having
parameters having 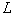 finite first moments that can be expressed as explicit functions
finite first moments that can be expressed as explicit functions 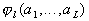 parameters
parameters  . Then, calculating the sample
. Then, calculating the sample 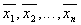
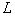 her first moments and equating them
her first moments and equating them 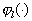 get the system of equations
get the system of equations
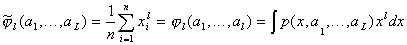 ,
,
from which estimates are determined  .
.
For one-dimensional normal law

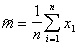 .
.
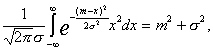
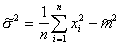 .
.
Comments
To leave a comment
Pattern recognition
Terms: Pattern recognition