Neocognitron

• 1 Principle of action
• 2Difference from cognitron
• 3Method of training
• 4 Species of neocognitron
• 5Notes
• 6Links
  
  

• Operating principle

  Differences from cognitron

  Cognitron and neocognitron have a certain similarity, but between them there are also fundamental differences associated with the evolution of the authors' research. Both samples are multi-level hierarchical networks, organized similarly to the visual cortex. At the same time, the neocognitron is more consistent with the model of the visual system described by Hubel DH and Wiesel TN ^[1] As a result, the neocognitron is a much more powerful paradigm in terms of its ability to recognize patterns regardless of their transformations, rotations, distortions and changes in scale. Like the cognitron, the neocognitron uses self-organization in the learning process, although the version ^[2] was described, in which controlled learning was used instead. ^[3]

  Teaching methods

• 

  Reception field. Skin neuron sposterіgaє for vidpovdnoy area

  Varieties of Neocognitron

• Over its long history, neocognitron has undergone many changes and modifications. So, for example, appeared:
  Neocognitron with two C-layers. [3]
  Neocognitron, the training of which passes through the method of back propagation of error [4]
  Neocognitron with selective attention in visual pattern recognition and associative recall. [five]

Neocognitron

In an effort to improve the cognitron, a powerful paradigm was developed, called the neocognitron [5–7]. While cognitron and neocognitron have a certain similarity, there are also fundamental differences between them related to the evolution of the authors' research. Both samples are multi-level hierarchical networks, organized similarly to the visual cortex. At the same time, the neocognitron is more consistent with the model of the visual system proposed in [10–12]. As a result, the neocognitron is a much more powerful paradigm in terms of the ability to recognize patterns, regardless of their transformations, rotation, distortion, and scale changes. Like cognitron, neocognitron uses self-organization in the learning process, although the version [9] was described, in which controlled learning was used instead.

Neocognitron is focused on modeling the human visual system. It receives two-dimensional images at the entrance, similar to images on the retina of the eye, and processes them in subsequent layers in the same way as it was found in the human visual cortex. Of course, in the neocognitron there is nothing limiting its use only for processing visual data, it is quite versatile and can be widely used as a generalized pattern recognition system.

In the visual cortex, nodes were found that respond to elements such as lines and angles of a certain orientation. At higher levels, nodes respond to more complex and abstract images such as circles, triangles, and rectangles. At even higher levels, the degree of abstraction increases until the nodes that respond to faces and complex shapes are determined. In general, nodes at higher levels get input from a group of low-level nodes and, therefore, respond to a wider area of ​​the visual field. The reactions of higher level nodes are less dependent on position and more resistant to distortion.

Structure

The neocognitron has a hierarchical structure focused on modeling the human visual system. It consists of a sequence of processing layers organized in a hierarchical structure (Fig. 10.8). The input image is fed to the first layer and transmitted through the planes corresponding to the subsequent layers until it reaches the output layer in which the recognizable image is identified.

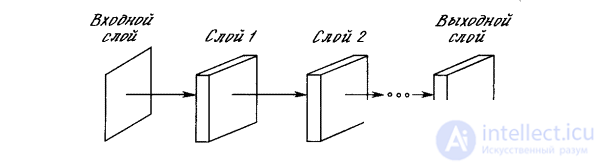
Fig. 10.8. The structure of the neocognitron layers

The structure of the neocognitron is difficult to represent in the form of a diagram, but is conceptually simple. To emphasize its multi-level (in order to simplify the graphical representation), use the analysis of the top level. The neocognitron is shown composed of layers, the layers consist of a set of planes and the planes consist of nodes.

Layers. Each layer of the neocognitron consists of two arrays of planes (Fig. 10.9). An array of planes containing simple nodes receives the outputs of the previous layer, selects certain images and then transfers them to an array of planes containing complex nodes, where they are processed in such a way as to make the selected images less positionally dependent.

The plane. Inside the layer, the planes of simple and complex nodes exist in pairs, that is, for the plane of simple nodes, there is one plane of complex nodes that processes its outputs. Each plane can be visually represented as a two-dimensional array of nodes.

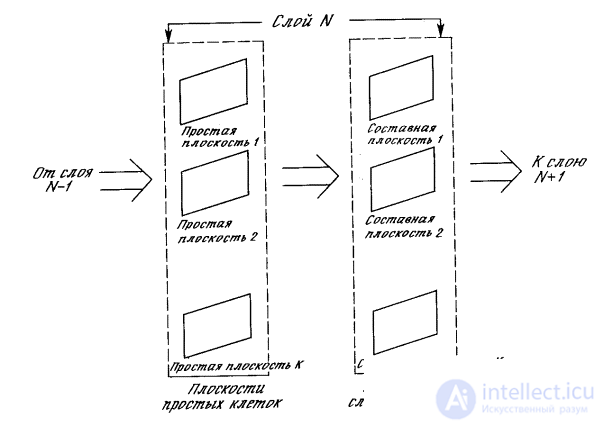
Fig. 10.9. The structure of the neocognitron planes

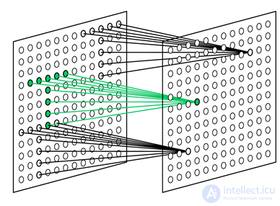
Simple knots. All nodes in a given plane of simple nodes respond to the same image. As shown in fig. 10.10, the plane of simple nodes represents an array of nodes, each of which is “tuned” to one specific input image. Each simple node is sensitive to a limited area of ​​the input image, called its receptive area. For example, all nodes in the upper plane of simple nodes in Fig. 10.10 react to "C". The node responds if “C” is found in the input image and if “C” is found in its receptive area.

In fig. 10.10, it is shown that other planes of simple nodes in this layer can react to a "C" turn by 90 °, others on a turn of 180 °, etc. If other letters are to be highlighted (and their distorted versions), additional planes are required for each of them.

The receptive areas of nodes in each plane of simple nodes overlap in order to cover the entire input image of this layer. Each node receives inputs from the corresponding regions of all planes of complex nodes in the previous layer. Consequently, a simple node responds to the appearance of its image in any complex plane of the previous layer, if it is inside its receptive area.

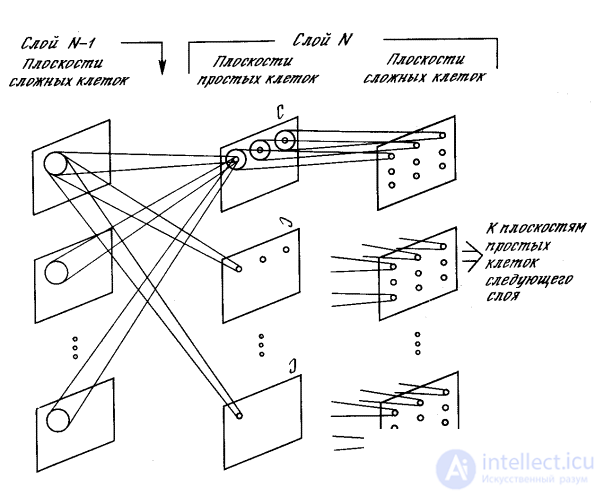
Fig. 10.10. Neocognitron system

Complex nodes. The task of complex nodes is to reduce the dependence of the response of the system on the position of the images in the input field. To achieve this, each complex node receives as an input image the outputs of a set of simple nodes from the corresponding plane of the same layer. These simple nodes cover a continuous area of ​​a simple plane, called the complex node's receptive area. The excitation of any simple node in this area is sufficient to excite this complex node. Thus, a complex node responds to the same image as simple nodes in the corresponding plane, but it is less sensitive to the position of the image than any of them.

Thus, each layer of complex nodes responds to a wider area of ​​the input image than it did in the previous layers. This progression increases linearly from layer to layer, leading to the required decrease in the positional sensitivity of the system as a whole.

Generalization

Each neuron in the layer close to the input reacts to certain images in a certain place, such as an angle with a specific orientation in a given position. As a result, each layer has a more abstract, less specific reaction than the previous one; the output layer responds to full images, showing a high degree of independence from their position, size and orientation in the input field. When used as a classifier, the complex node of the output layer with the highest response implements the selection of the corresponding image in the input field. Ideally, this selection is insensitive to position, orientation, size or other distortion.

Calculations

Simple nodes in a neocognitron have exactly the same characteristics as those described for the cognitron, and use the same formulas to determine their output. Here they are not repeated.

The braking node produces an output proportional to the square root of the weighted sum of the squares of its inputs. Note that the inputs to the braking node are identical to the inputs of the corresponding simple node and the area includes the response area in all complex planes. In symbolic form

,

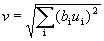where v is the output of the braking unit; i is the area above all complex nodes with which the braking node is connected; b _i is the weight of the i- th synaptic connection from the complex node to the braking node; u _i is the output of the i- th complex node.

The weights b _i are chosen monotonously decreasing with increasing distance from the center of the reaction region, and the sum of their values ​​should be equal to one.

Training

Only simple nodes have custom weights. These are the weights of the links connecting the node with the complex nodes in the previous layer and having synapses of variable strength, which are configured in such a way as to develop the maximum response to certain stimulating properties. Some of these synapses are stimulating and tend to increase the output of the nodes, while others are inhibitory and reduce the output of the node.

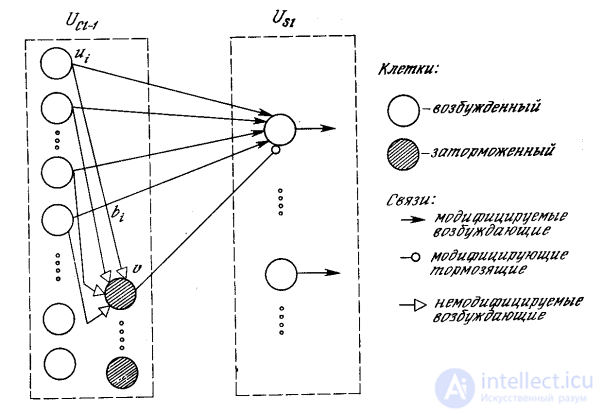
Fig. 10.11. Communication from complex cells of the same level
to simple cells of the next level

In fig. 10.11 shows the complete structure of synaptic connections between a simple node and complex nodes in the previous layer. Each simple node responds only to a set of complex nodes within its receptive area. In addition, there is a braking node that responds to the same complex nodes. The weights of the synapses of the decelerating node are not trained, they are chosen so that the node responds to the average value of the outputs of all the nodes to which it is connected. The only inhibitory synapse from the inhibitory node to the simple node is learned, like other synapses.

Teaching without a teacher. To train a neocognitron, an image is fed to the input of the network, which needs to be recognized, and the weights of the synapses are adjusted layer by layer, starting with a set of simple nodes closest to the input. The magnitude of the synaptic connection from each complex node to a given simple node increases if and only if the following two conditions are satisfied:

one)         complex node responds;

2)         a simple node responds more strongly than any of its neighbors (within its area of ​​competition).

Thus, a simple node learns to respond more strongly to the images that appear most often in its receptive area, which is consistent with the results of research obtained in experiments with kittens. If a recognizable image is not present at the input, the braking unit prevents accidental excitation.

The mathematical description of the learning process and the method of implementing lateral inhibition are similar to those described for the cognitron; therefore, they are not repeated here. It should be noted that the outputs of simple and complex nodes are analog, continuous and linear, and that the learning algorithm implies their non-negativity.

When a simple node is selected, the weight of the synapses of which must be increased, it is considered as a representative of all the nodes in the plane, causing an increase in their synaptic connections on the same image. Thus, all the nodes in the plane are trained to recognize the same properties, and after training they will do it regardless of the position of the image in the field of complex nodes in the previous layer.

This system has valuable self-healing ability. If this node fails, another node will be found that reacts more strongly, and this node will be trained to recognize the input image, thereby blocking the actions of its failed comrade.

Training with a teacher. In [3] and [8], self-organizing unmanaged learning is described. Along with these impressive results, reports were published on other experiments using training with a teacher [9]. Here the required reaction of each layer is determined in advance by the experimenter. The weights are then adjusted using conventional methods to generate the desired reaction. For example, the input layer was configured to recognize line segments in different orientations in much the same way as the first processing layer of the visual cortex. Subsequent layers are trained to respond to more complex and abstract properties until the desired image is selected in the output layer. When processing a network that perfectly recognizes handwritten Arabic numerals, the experimenters refused to achieve biological likelihood, paying attention only to achieving the maximum accuracy of the system results.

The implementation of training. In normal configurations, the receptive field of each neuron increases with the transition to the next layer. However, the number of neurons in the layer will decrease when moving from input to output layers. Finally, the output layer has only one neuron in the plane of complex nodes. Each such neuron represents a specific input image that the network was trained on. In the process of classification, the input image is fed to the input of the neocognitron and the outputs are calculated layer by layer, starting with the input layer. Since only a small part of the input image is fed to the input of each simple node in the input layer, some simple nodes register the presence of characteristics that they are trained in and are excited. In the next layer, more complex characteristics are distinguished as certain combinations of outputs of complex nodes. Layer by layer properties are combined in an ever-increasing range; more general characteristics stand out and positional sensitivity decreases.

In the ideal case, only one neuron of the output layer should be excited. In reality, several neurons with different powers will usually be excited, and the input image must be determined taking into account the ratio of their outputs. If the lateral braking force is used, only the neuron with the maximum output will be excited. However, this is often not the best option. In practice, a simple function from a small group of most highly excited neurons will often improve the classification accuracy.

CONCLUSION

Both cognitron and neocognitron are very impressive in terms of the accuracy with which they model the biological nervous system. The fact that these systems show results that mimic some aspects of a person’s learning and cognition abilities suggests that our understanding of brain functions is approaching a level that can bring practical benefits.

Neocognitron is a complex system and requires substantial computational resources. For these reasons, it seems unlikely that such systems implement an optimal engineering solution to today's pattern recognition problems. However, since 1960, the cost of computing has decreased twice every two to three years, a trend that is likely to continue for at least the next ten years. Despite the fact that many approaches that seemed unrealizable a few years ago are generally accepted today and may turn out to be trivial in a few years, the implementation of neocognitron models on universal computers is futile. It is necessary to achieve thousand-fold improvements in the cost and performance of computers due to the specialization of the architecture and the introduction of VLSI technology to make the neocognitron a practical system for solving complex pattern recognition problems, but neither this nor any other model of artificial neural networks should be rejected solely on the basis of their high computational requirements.