Lecture
If, in the previously considered recognition methods, the decision on whether an object was in one form or another was carried out immediately along the entire set of features, then in this section we will discuss the case of their consistent measurement and use.
Let be 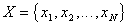 . First, the object is measured
. First, the object is measured 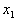 and on the basis of this information, the question of attributing this object to one of the images is decided. If this can be done with a sufficient degree of confidence, then other signs are not measured and the recognition procedure ends. If there is no such certainty, then the sign is measured.
and on the basis of this information, the question of attributing this object to one of the images is decided. If this can be done with a sufficient degree of confidence, then other signs are not measured and the recognition procedure ends. If there is no such certainty, then the sign is measured. 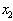 and the decision is made in two ways:
and the decision is made in two ways: 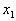 and
and 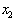 . Further, the procedure is either terminated or the sign is measured.
. Further, the procedure is either terminated or the sign is measured. 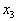 and so on until either a decision is made to classify the object to any image, or all
and so on until either a decision is made to classify the object to any image, or all 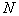 signs.
signs.
Such procedures are extremely important in cases where the measurement of each of the signs requires a significant expenditure of resources (material, temporary, etc.).
Let be 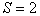 and known
and known 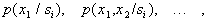
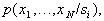 Where
Where 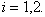 Note that if the distribution is known
Note that if the distribution is known 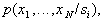 then all distributions of smaller dimension are known (the so-called marginal distributions). For example,
then all distributions of smaller dimension are known (the so-called marginal distributions). For example,
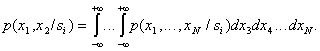

Let measured 
 signs. Build likelihood ratio
signs. Build likelihood ratio 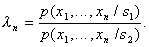 If a
If a 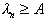 then the object is attributed to the image
then the object is attributed to the image 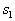 , if a
, if a 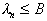 then to the image
then to the image 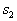 . If
. If 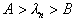 then the sign is measured
then the sign is measured  and calculate the likelihood ratio
and calculate the likelihood ratio 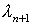 etc.
etc.
It is clear that the thresholds  and
and 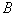 associated with the permissible probability of recognition errors. Achieving inequality
associated with the permissible probability of recognition errors. Achieving inequality 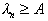 we strive to ensure that the probability of correctly assigning the object of the first image to
we strive to ensure that the probability of correctly assigning the object of the first image to 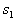 Was in
Was in 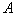 times more than the erroneous assignment of the object of the second image to
times more than the erroneous assignment of the object of the second image to 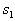 , i.e
, i.e 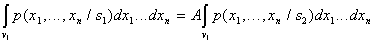 or
or 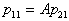 . Insofar as
. Insofar as 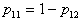 then
then 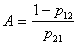 (upper threshold). Similar reasoning is carried out to determine
(upper threshold). Similar reasoning is carried out to determine 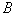 . Achieving inequality
. Achieving inequality 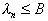 we strive to ensure that the probability of correctly assigning the object of the second image to
we strive to ensure that the probability of correctly assigning the object of the second image to  Was in
Was in 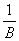 times more than the incorrect assignment of the object of the first image to
times more than the incorrect assignment of the object of the first image to 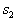 , i.e
, i.e
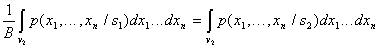 ,
,
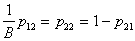 ,
,
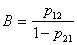 (lower threshold).
(lower threshold).
In a consistent procedure for measuring signs, a very useful property of these signs is their statistical independence. Then 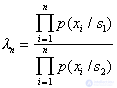 and there is no need to store (and most importantly, build) multidimensional distributions. In addition, it is possible to optimize the sequence of the measured signs. If they are ranked in descending order of classification informativity (the amount of discriminating information) and a consistent procedure is organized in accordance with this ranking, the number of measured signs can be reduced on average.
and there is no need to store (and most importantly, build) multidimensional distributions. In addition, it is possible to optimize the sequence of the measured signs. If they are ranked in descending order of classification informativity (the amount of discriminating information) and a consistent procedure is organized in accordance with this ranking, the number of measured signs can be reduced on average.
We have reviewed the case of 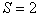 (two images). If a
(two images). If a 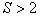 , then likelihood relationships can be built
, then likelihood relationships can be built 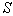 , for example of this type:
, for example of this type: 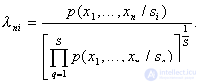 Stopping boundary (threshold) for
Stopping boundary (threshold) for 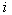 th image is chosen equal
th image is chosen equal 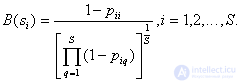 If a
If a 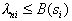 then
then 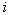 th image is discarded and built
th image is discarded and built 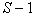 likelihood ratios and thresholds
likelihood ratios and thresholds 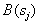 . The procedure continues until only one image remains unreleased or all of them have been exhausted.
. The procedure continues until only one image remains unreleased or all of them have been exhausted. 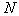 signs. If in the latter case more than one image remained unreleased, the decision is made in favor of the one for which the likelihood ratio
signs. If in the latter case more than one image remained unreleased, the decision is made in favor of the one for which the likelihood ratio 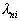 as much as possible.
as much as possible.
If there are two images ( 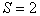 ) and the number of signs is not limited, then a sequential procedure with probability 1 ends in a finite number of steps. It is also proved that given
) and the number of signs is not limited, then a sequential procedure with probability 1 ends in a finite number of steps. It is also proved that given 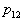 and
and 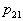 considered procedure with the same informativeness of various signs will give a minimum of the average number of steps. For
considered procedure with the same informativeness of various signs will give a minimum of the average number of steps. For 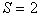 Vald introduced a sequential procedure and called it a successive criterion for the ratio of probabilities (c.to.v.).
Vald introduced a sequential procedure and called it a successive criterion for the ratio of probabilities (c.to.v.).
For 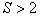 optimal procedure is not proven.
optimal procedure is not proven.
With known prior probabilities, you can implement a Bayesian sequential procedure, and if you know the costs of character measurements and the matrix of penalties for incorrect recognition, then the sequential procedure can be stopped to minimize the average risk. The point here is to compare the losses caused by recognition errors when the procedure is terminated, and the expected losses after the next measurement plus the cost of this measurement. Such a problem is solved by the dynamic programming method if successive measurements are statistically independent. More detailed information on the optimization of the Bayes sequential procedure can be found in the recommended literature [8].
Comments
To leave a comment
Pattern recognition
Terms: Pattern recognition