Hierarchical recognition systems

When recognizing complex objects (words of speech, names of cities, rivers, lakes, etc. on geographical maps; composite images, which are a combination of certain geometric primitives), it is advisable to use hierarchical recognition procedures. To some extent we have dealt with this approach when considering linguistic (structural) recognition methods. As the name implies, a feature of hierarchical recognition procedures is their multi-level. At the lower level, elementary images (primitives) are recognized, at higher levels - composite images. Naturally, the number of levels can be different. For definiteness, we will consider a two-level recognition system.

There are two types of two-level recognition system. The first is characterized by the presence of a natural temporal or spatial sequence of images of the first level, coming in for recognition to the second level. For example, it may be a sequence of phonemes when recognizing oral words or a sequence of letters when recognizing names on a geographic map. Here, the structural connections between the images of the first level are extremely simplified and are described by order. In the second type of two-level recognition systems, the structural connections between the images of the first level are more complex. For example, if letters are recognized by a two-level system, then the images of the first level (straight line segments, arcs) are connected to each other on a plane according to some rules more complicated than simple following. We considered this option earlier when it came to linguistic methods of recognition.

In this section, we will focus on the case when a natural sequence of images of the first level comes to the second recognition stage.

So, the second stage does not receive the object itself, but the results of recognition of its elements at the first stage. 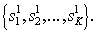Length 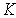such sequences are generally different. Alphabet of images 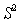The second recognition level is a set of sequences of first-level images and can be significantly larger than the alphabet of first-level images. For example, tens of thousands of recognizable words can consist of 32 letters of the Russian alphabet.

If pattern recognition at the first level were faultless, then recognition at the second level would be reduced to the choice from the alphabet of the second level of the sequence that matched the sequence obtained at the output of the first level of the recognition system. However, in practice, errors are inevitable in recognition, including in hierarchical systems, and in the latter at various levels of recognition. If mistakes are made on the first level, then a sequence that does not coincide with any of the images included in the alphabet of the second level can be received at the input of the second level; nevertheless, some decision must be made. Possible, for example, such a deterministic version. From the alphabet 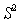those sequences are selected that contain as many elements as they are contained in the sequence shown for recognition. Then the recognizable sequence is superimposed on the selected from 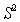sequence and count the number of non-matching elements. The assignment to a particular image is carried out according to the minimum number of mismatched elements. Such an approach is, to a certain extent, an analogue of the previously considered method of minimum distance to the standard, only the metrics used are different.

Here we believed that recognition errors made at the first level distort only one or another element of the sequence, without affecting their total number. In practice, however (in particular, when recognizing oral words), the number of elements in the sequence may be distorted: unnecessary false elements appear or objectively available elements are skipped. In this case, there are quite effective recognition algorithms implemented at the second stage of hierarchical systems. Their study is beyond the scope of this course.

Consider a statistical approach to recognition in a two-level hierarchical system (Fig. 26). Let images be recognized on the first level 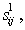Where 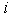- position number in sequence 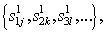issued by the first stage for recognition on the second stage; 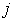- the number of the competing image of the first stage on 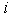th position in the sequence.

The fact is that in hierarchical recognition systems, it is advisable at intermediate steps not to make a final decision about the belonging of an object to one or another image, but to give a set of variants with their posterior probabilities. This set must be such that the correct solution is included in it with a probability close to one. If all competing solutions of all positions are considered as vertices of the graph, enter formally the initial 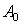and final 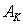vertices, connect vertices by arcs, as shown in Fig. 26, we get a directed graph without cycles. The image 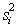The second level of recognition corresponds to a well-defined path in the graph. In fig.26 the path corresponding to the sequence is marked with thickened arcs. 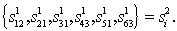In the fourth column of competing images of the first stage there is - empty vertex corresponding to the absence of elements of its column in the sequence. The presence of such vertices allows you to remove from the sequence of "false" elements that appeared as a result of recognition errors in the first stage. Of course, with this top the corresponding posterior probability must be correlated.

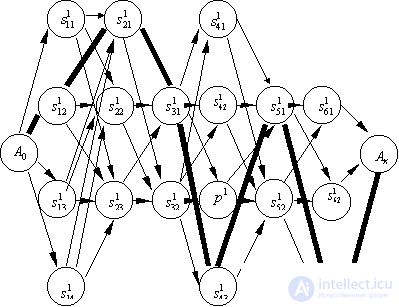
Fig. 26. Oriented graph illustrating
recognition process in a two-step system

Images (sequences) from the alphabet of the second stage are superimposed on the constructed graph, and the one that has the maximum a posteriori probability 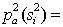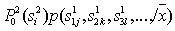It is adopted as a decision at the top stage.

Here 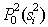- a priori probability of the image 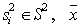- vector of parameters characterizing the objects at the input of the first recognition stage.

If we talk about a sequence of letters, then each of them is recognized independently of the others, therefore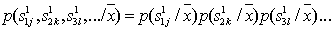

The procedure described is applicable in cases where the alphabet is fixed. 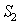. In word processing, this requirement is often not met. For example, this is the case when entering text from a scanner and converting an image of a page with text into a text file. Since the entered texts have arbitrary content, it is hardly possible to fix the dictionary and there is no special need for that. After all, the user needs only a sequence of recognized letters, punctuation marks and spaces. In other words, it would be possible to confine ourselves only to the first step of recognition. However, the results of such recognition require significant editorial editing, since there are errors in attributing the input objects to a particular image. For example, with the likelihood of incorrect recognition 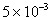on one typewritten page of a text file there will be on average 10-12 grammatical errors. Very poor literacy rate. It can be enhanced by at least partial modeling of the second stage of recognition. For example, not having a fixed alphabet of words, you can fix the alphabet of two-letter, three-letter, etc. sequences. The number of such sequences for each language is fixed, and their a priori probabilities (at least for two letters) weakly depend on the vocabulary. In fig. 26 is a graph that can be used for two-letter sequences. The use of a larger number of letters leads to a significant complication of the graph without changing the principle of calculations, so we limit ourselves to considering the two-letter version.

If the system recognizes words in a fixed alphabet 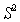, then write down the prior probability of the word 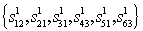could be as follows:

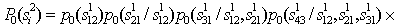
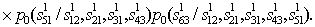
If we restrict ourselves to using a priori probabilities of only two-letter combinations, then

.

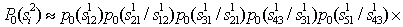
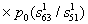Instead of the product, you can operate with a sum, if you move from probabilities to their logarithms.

So, if each arc is assigned a length equal to 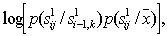then the most likely sequence of letters will correspond to the path of the maximum length on the graph. This path is not difficult to find by methods known in graph theory.

The effectiveness of this approach to correct the errors of the first step of recognition due to language redundancy is confirmed by practical tests. Yes it is in some cases clear and speculative. For example, when recognizing a sequence of letters, the considered algorithm will certainly detect, and in most cases will correct, such errors as "vowel - hard (soft) sign", "space - hard (soft) sign", "soft sign - e" and a number others.