Lecture
We consider this approach separately because it is quite versatile in its properties. In addition to estimating (restoring) distributions, it allows you to simultaneously solve the problem of taxonomy, optimized management of a sequential feature measurement procedure, even if they are statistically dependent, makes it easier to evaluate the informativeness of features and to solve some experimental data analysis problems.
The method is based on the assumption that the unknown (recoverable) distribution of the characteristic values of each image is well approximated by a mixture of basic distributions of a fairly simple and previously known form.
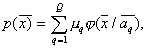
Where 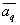 - set (vector) of parameters
- set (vector) of parameters 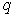 of the base distribution,
of the base distribution, 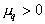 - weights that satisfy the condition
- weights that satisfy the condition 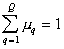 . In order not to overload the formula, it omits the index of the image number, which is described by this distribution of attribute values.
. In order not to overload the formula, it omits the index of the image number, which is described by this distribution of attribute values.
The representation of the unknown distribution as a series is used, for example, in the method of potential functions. However there  are elements of a complete orthogonal system of functions. On the one hand, this is good, because the calculation
are elements of a complete orthogonal system of functions. On the one hand, this is good, because the calculation  first values
first values  guarantees the minimum of the standard deviation of the restored distribution from the true one. But in other way,
guarantees the minimum of the standard deviation of the restored distribution from the true one. But in other way, 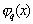 are not distributions, can be alternating, that when
are not distributions, can be alternating, that when 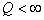 usually leads to an unacceptable effect when for some values
usually leads to an unacceptable effect when for some values 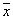 recovered distribution
recovered distribution  is negative. Attempts to avoid this effect are not always successful. This disadvantage is devoid of the considered approach, when the desired distribution is represented by a mixture of basic ones. Wherein
is negative. Attempts to avoid this effect are not always successful. This disadvantage is devoid of the considered approach, when the desired distribution is represented by a mixture of basic ones. Wherein  called the component component distributions, and
called the component component distributions, and 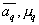 and
and 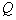 - its parameters. This approach with obvious merits has disadvantages. In particular, the solution of the problem of estimating the mixture parameters is, generally speaking, multi-extremal, and there are no guarantees that the solution found is in global extremum, if we exclude an unacceptable in practice complete enumeration of the mixture splitting into components.
- its parameters. This approach with obvious merits has disadvantages. In particular, the solution of the problem of estimating the mixture parameters is, generally speaking, multi-extremal, and there are no guarantees that the solution found is in global extremum, if we exclude an unacceptable in practice complete enumeration of the mixture splitting into components.
Concepts such as “mixture”, “component” are usually used in solving taxonomy problems, but this does not interfere with the description in the form of a mixture of a fairly general form of the distribution of the values of attributes of a particular image. The approximation method is intermediate between parametric and nonparametric estimation of distributions. Indeed, the sample has to evaluate the values of the parameters. 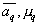 and
and 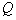 , and at the same time, the type of distribution law is not known in advance; only the most general restrictions are imposed on it. For example, if the component is a normal law, then the probability density
, and at the same time, the type of distribution law is not known in advance; only the most general restrictions are imposed on it. For example, if the component is a normal law, then the probability density 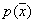 should not be zero for all
should not be zero for all 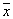 and be fairly smooth. If the component is a binomial law, then
and be fairly smooth. If the component is a binomial law, then 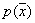 can be almost any discrete distribution.
can be almost any discrete distribution.
At the same time, it is not possible to determine the parameters of the mixture using classical parametric estimation methods (for example, the method of moments or maximum likelihood function) with rare exceptions (special cases). In this regard, it is advisable to refer to the methods used in solving taxonomy problems. 
As components, it is convenient to use binomial laws for discrete features and normal probability densities for continuous features, since the properties and theory of these distributions are well studied. In addition, they, as practical applications show, as a component adequately adequately describe a very wide class of distributions.
The normal law, as is known, is characterized by a vector of mean values of features and a covariance matrix. A special place in a number of tasks is occupied by normal laws with diagonal covariance matrices (in the components, the signs are statistically independent). At the same time, it is possible to optimize a consistent procedure for measuring signs, even if in the restored distribution 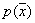 signs are addicted. Consideration of this issue is beyond the scope of the course. Those interested can refer to the recommended literature [2].
signs are addicted. Consideration of this issue is beyond the scope of the course. Those interested can refer to the recommended literature [2].
To facilitate the understanding of the approximation method, we will consider a simplified version, namely, one-dimensional distributions.
So,
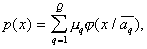
Where |
|
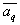 - vector of parameters of the base distribution (components),
- vector of parameters of the base distribution (components),
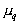 - weight coefficient
- weight coefficient 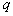 components,
components,
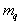 - expected value
- expected value 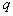 normal component,
normal component,
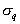 - standard deviation
- standard deviation 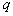 normal component,
normal component,
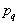 - parameter
- parameter 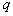 th binomial component
th binomial component
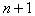 - the number of graduations of a discrete characteristic,
- the number of graduations of a discrete characteristic,
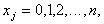
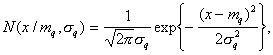
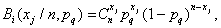
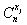 - number of combinations of
- number of combinations of 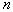 by
by 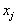 .
.
When large enough 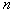 instead of the binomial law, you can use the normal one.
instead of the binomial law, you can use the normal one.
Now we have to evaluate the values of the parameters. If we consider a mixture of normal laws, then it should be noted that the maximum likelihood method is not applicable when all the parameters of the mixture are unknown. In this case, you can use reasonably organized iterative procedures. Consider one of them.
To begin, fix 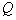 , that is, we will consider it given. Each object
, that is, we will consider it given. Each object 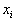 the samples we assign the posterior probability
the samples we assign the posterior probability 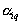 his accessories
his accessories 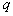 th component of the mixture:
th component of the mixture:
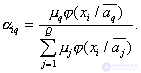
It is easy to see that for all 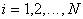 conditions are met
conditions are met 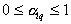 and
and  . If known
. If known 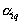 for all
for all 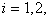
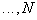 then you can define
then you can define 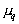 maximum likelihood method
maximum likelihood method 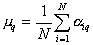 .
.
Likelihood function 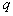 the th components of the mixture will be defined as follows
the th components of the mixture will be defined as follows 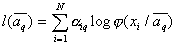 and maximum likelihood estimates
and maximum likelihood estimates 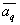 can be obtained from the equation
can be obtained from the equation 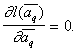
So knowing 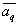 and
and 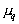 can define
can define 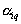 and vice versa knowing
and vice versa knowing 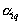 can define
can define 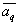 and
and 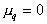 , that is, the parameters of the mixture. But neither is unknown. In this regard, we use the following procedure of successive approximations:
, that is, the parameters of the mixture. But neither is unknown. In this regard, we use the following procedure of successive approximations:
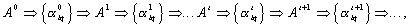
Where  ,
, 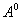 - arbitrarily specified initial values of the parameters of the mixture, the superscript is the iteration number in a sequential calculation procedure.
- arbitrarily specified initial values of the parameters of the mixture, the superscript is the iteration number in a sequential calculation procedure.
It is known that this procedure is convergent and 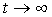 the limits are estimates of unknown parameters.
the limits are estimates of unknown parameters. 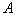 mixtures giving maximum likelihood functions
mixtures giving maximum likelihood functions
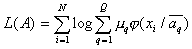 ,
,
and 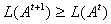 and
and 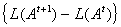 tends to zero at
tends to zero at 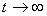 .
.
For one-dimensional normal law
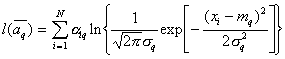 .
.
Solving the equation 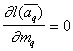 and
and 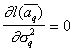 get for
get for 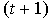 th step
th step 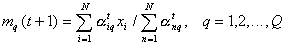 ,
, 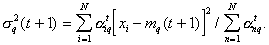
After completing the sequential procedure,  . The corresponding computational formulas for multidimensional normal distributions can be found in [2].
. The corresponding computational formulas for multidimensional normal distributions can be found in [2].
The values of the parameters obtained as a result of the sequential procedure considered are estimates of the maximum likelihood of both the component and the mixture as a whole.
If a  has several maxima, the iteration process depending on the given initial values
has several maxima, the iteration process depending on the given initial values  converges to one of them, not necessarily global. To overcome this drawback inherent in almost all methods of estimating the parameters of multidimensional distributions (at least, mixtures) is quite difficult. In particular, you can repeat the sequential procedure several times with different
converges to one of them, not necessarily global. To overcome this drawback inherent in almost all methods of estimating the parameters of multidimensional distributions (at least, mixtures) is quite difficult. In particular, you can repeat the sequential procedure several times with different  and choose the best solution. Selection of various
and choose the best solution. Selection of various 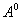 carried out either randomly or using various kinds of procedures. Rate of convergence
carried out either randomly or using various kinds of procedures. Rate of convergence 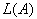 the higher the higher, the more strongly the components are separated in the attribute space and the closer the selected
the higher the higher, the more strongly the components are separated in the attribute space and the closer the selected 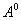 to meanings
to meanings 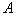 corresponding to maximum likelihood function.
corresponding to maximum likelihood function.
We considered a method for estimating the parameters of a mixture with a fixed number of components. 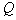 . But in the approximation method and
. But in the approximation method and 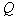 should be determined by optimizing any criterion. The following approach is proposed. Parameters are evaluated consistently.
should be determined by optimizing any criterion. The following approach is proposed. Parameters are evaluated consistently. 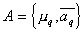 at
at 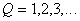 . From the resulting series
. From the resulting series 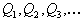 selected in some sense the best value
selected in some sense the best value 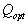 .
.
We use the measure of uncertainty K. Shannon 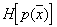 for searching
for searching 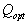 :
:
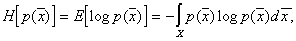
Where 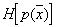 - distribution entropy
- distribution entropy 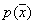 ,
,
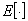 - a sign of mathematical expectation
- a sign of mathematical expectation
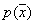 - probability density values of continuous features.
- probability density values of continuous features.
With a consistent increase in values 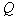 There are two trends:
There are two trends:
· A decrease in entropy due to the separation of the sample into parts with a decreasing scatter of the values of the observed values 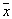 inside subsamples (mixture component);
inside subsamples (mixture component);
· An increase in entropy due to a decrease in the volume of subsamples and the associated increase in statistics describing the variation of values 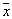 .
.
The presence of these two trends determines the existence 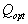 by the criterion of the smallest value of the differential entropy (Fig. 23). In order to use this criterion in practice, it is necessary to explicitly express the evaluation of the components of the mixture through the volume of the subsample that forms this component. Such relations are obtained for normal and binomial distributions. For simplicity, consider a one-dimensional normal distribution. We use its Bayesian estimate.
by the criterion of the smallest value of the differential entropy (Fig. 23). In order to use this criterion in practice, it is necessary to explicitly express the evaluation of the components of the mixture through the volume of the subsample that forms this component. Such relations are obtained for normal and binomial distributions. For simplicity, consider a one-dimensional normal distribution. We use its Bayesian estimate.
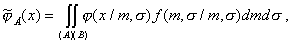
Where 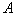 - domain
- domain 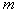 ,
,
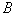 - domain
- domain 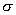 ,
,
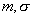 - selective estimates
- selective estimates 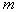 and
and 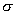 .
.
According to the Bayes formula
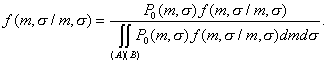
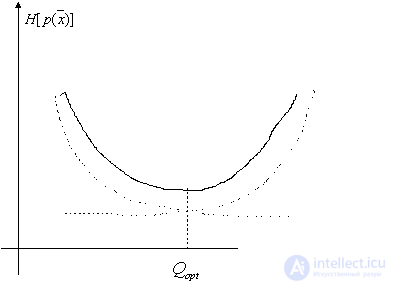
Fig. 23. Illustration of trends shaping 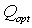
If the prior distribution is 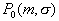 unknown, it is advisable to use a uniform distribution throughout the region
unknown, it is advisable to use a uniform distribution throughout the region
Omitting all the calculations that are given in [2], we only report that a distribution is obtained that is not Gaussian, but asymptotically converges to it (for 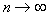 ). Average value
). Average value 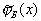 equal to the average value determined by the sample, and the variance is equal to the sample variance
equal to the average value determined by the sample, and the variance is equal to the sample variance 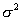 multiplied by the coefficient
multiplied by the coefficient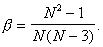
It can be shown that it is 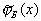 well approximated by a normal law with a mathematical expectation equal to
well approximated by a normal law with a mathematical expectation equal to 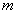 - the sample mean, and a dispersion equal to the sample dispersion
- the sample mean, and a dispersion equal to the sample dispersion 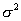 multiplied by
multiplied by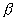 . Как видно из формулы,
. Как видно из формулы, 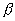 стремится к единице при
стремится к единице при 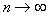 , возрастает с уменьшением
, возрастает с уменьшением 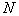 и накладывает ограничения на объём выборки
и накладывает ограничения на объём выборки  (рис. 24).
(рис. 24).
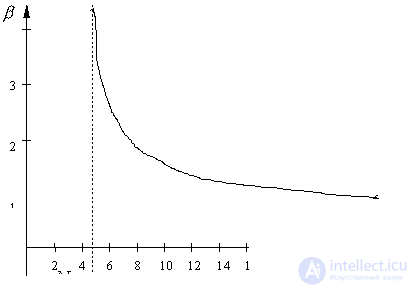
Fig. 24. Зависимость поправочного коэффициента b
от объёма выборки N
Таким образом, нам удалось в явной форме выразить зависимость параметров компонент смеси от объёма подвыборок, что, в свою очередь, позволяет реализовать процедуру поиска 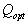 .
.
Объём подвыборки для q -й компоненты смеси определяется по формуле 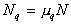 .
.
Итак, рассмотрен вариант оценки параметров смеси. Он не является статистически строго обоснованным, но все вычислительные процедуры опираются на критерии, принятые в математической статистике. Многочисленные практические приложения аппроксимационного метода в различных предметных областях показали его эффективность и не противоречат ни одному из допущений, изложенных в данном разделе.
Более подробное и углублённое изложение аппроксимационного метода желающие могут найти в рекомендованной литературе [2], [4].
Comments
To leave a comment
Pattern recognition
Terms: Pattern recognition