Reception and processing of signals in the background noise

Radio receivers and other radio devices have their own electrical noise. Noise interference may be supplied to radio systems.

In linear radio devices, the principle of superposition can be applied: the passage of signals and noise is considered separately. Figure 1 illustrates this principle.

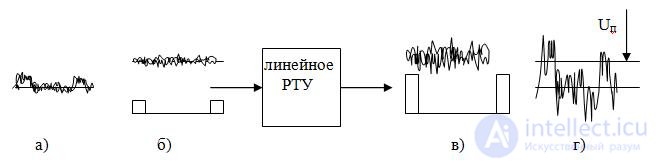
Fig. 1. Adjective mixture and superposition principle

  The additive mixture of signal and noise at the input of a radio engineering device (MOUTH) has the form a). It can be considered separately: separate signal and noise (option b). The signal and noise passes the linear MOUTH separately and separately appear at the output (option c). Although this additive mixture actually looks on an oscilloscope in option d), which can be obtained by adding the components of option c).

  The principle of separate consideration of the signal and noise is not acceptable where the mixture at the input of the MOUTH is multi-active, or there are non-linear links in the MOUTH itself or an amplitude restriction process occurs.

  The first step in receiving signals is the detection procedure. The quality of detection is characterized by the probabilities of the correct    and not correct detection. The first indicator is usually associated with the probability of detecting P _about , the second with the probability of a false alarm P _Lt. Although there are indicators such as the probability of missing a signal P _ar. Signal skip and detection are opposite events.

                                                         Р _об = 1- Р _прп

  Signal detection occurs when it overcomes a certain threshold U _p , as shown in Fig. 1d. If the threshold is low, then noise emissions can overcome it. This is a false alarm, as the occurrence of a signal is recorded. Too high a level will not allow detecting weak signals. There will be skips of signals. Choosing a threshold level is not an easy radio task.

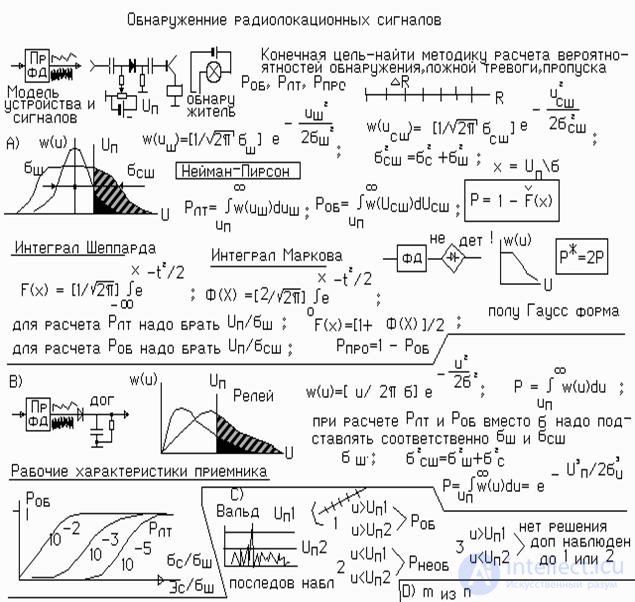
        Fig. 2. Radar signal detection - statistical task

  In modern radar, automatic detectors detect signals in noise. Signals from both the output of the phase detectors and the amplitude output can be fed to their input . In both cases, the probabilistic problem is solved.

  Neumann - Pearson single-threshold detector. In the case when the additive mixture of signal and noise exceeds the threshold, registration (detection) occurs. This type of detection is called "correct detection" or simply "detection." Its probability is denoted by P _about .

If the noise exceeds the threshold level, then a false signal registration will occur, although there is no noise in it. This option of registration is called “incorrect detection” or “false alarm”. P _lt . The probabilities P _o and P _lt fully characterize the consumer quality of the radar when operating in the target search mode.

  The radar phase detector detects instantaneous values ​​of the reflected signal.    The signal model can be a normal stationary process with zero mean value.    

  The additive mixture of signal and noise has the same model.

  The probability densities of the amplitudes of the noise, the signal and the additive mixture will have the form of a Gaussian curve, as shown in the figure. Moreover, the dispersion of the mixture s _ssh ^{2 is} calculated by summing the dispersions of the components.

                                                             s us ² =    s _с ² + s _ш ²

  The probability of detection of P _about    calculated by integrating the law of distribution of the mixture of noise and signal w ( u _ssh ) from the relative threshold level x = U _p / s us    to infinity.

  The probability of a false alarm P   _{lt is} calculated similarly. But under the integral should be the distribution of noise w ( u ). In this case, x = U _p / s _w .

  Unfortunately, the integral of the Gauss function is not taken directly. Therefore, it is necessary to use the results of the numerical integration of the Sheppard integral F ^ ( x ) or its version - the Markov integral.

  To get the results, it is enough to calculate the value x = U _p / s us    or x = U _p / s _w   accordingly, using the Sheppard or Markov probability integral tables, find the necessary probabilities P _about   and    R   _lt .

  Integrals of Markov probabilities can be found, for example, in the reference book on mathematics by Bronstein and Semendyayev.

  Amplitude detector highlights the envelope of the signals. In accordance with the adopted model, the distribution law of the Rayleigh amplitudes. The calculation of probabilities is carried out similarly to the above described method. The integral of the Rayleigh function is taken. Therefore probabilities

P _about   and    R   _{lt are} calculated without problems _.

  In addition to the Neumann-Pearson detector, there are more advanced ones, including Wald detectors, minimax, logical, and others.