Lecture
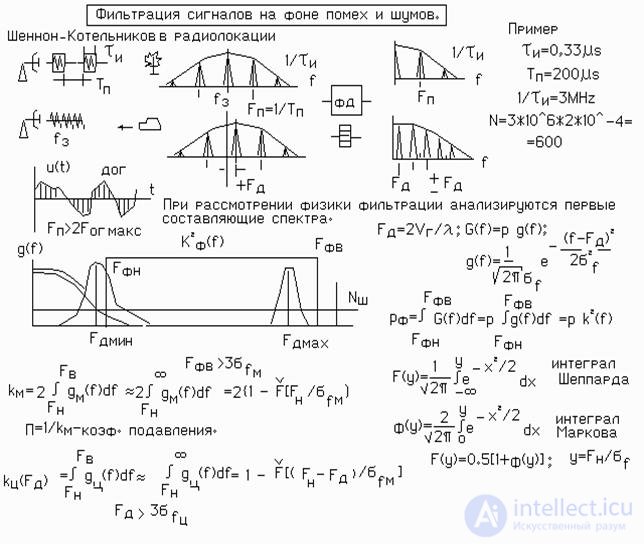
Fig. 2.5. Reducing the effects of noise and passive interference.
Radar target search has to be carried out against the background of thermal noise of the receiver and passive interference from the terrain. The effect of this interference can be great. Thus, when searching for ground targets, the reflection of signals from the terrain is so strong that the probability of detection may drop to zero. Filtering is used to combat interference .
In the radar of continuous radiation, the spectra of the radar signals reflected from the targets and the terrain and allocated at the output of the phase detector lie in the sound frequency range from 0 to 2-3 KHz. They are defined uniquely.
In pulsed radar spectra have lined character, since the signals are periodic.
Moreover, side components are formed around each harmonic, which are similar to those formed in the low-frequency region of a continuous-radiation radar.
The calculation of the results of the filters is much more complicated.
The calculations can be simplified using the Shannon-Kotelnikov theorem. In accordance with it, the difference between the pulsed radar and the radar of continuous radiation is as follows. The radar of continuous radiation receives information from the target continuously, and
pulse - discrete. But if the pulse frequency of the radar is greater than The width of the line low frequency spectrum, from the point of view of information content, there is no difference between radars . Since the spectra to the left and right of the harmonics are similar to the spectrum located near zero, it is sufficient to consider the principle of the operation of the filtering units in the low-frequency region.
The spectrum of a random stationary signal can be represented as a probability density.
power on the frequency axis. For a model of a normal stationary process, the Gaussian spectra form . Considering the spectrum as the law of distribution of a random variable, one can greatly simplify the calculations of the signals at the output of the filters. Taking the integral of the spectrum from
the values of the lower cutoff frequency response of the filter to the upper cutoff, we obtain the transfer coefficient.
Since the integral is not taken directly, we use the results of numerical integration. Table values of probability integrals are given in reference books in mathematics as Sheppard and Markov integrals . ( c . lecture 2.4., guidelines for course design radar).
Comments
To leave a comment
Radio Engineering Systems
Terms: Radio Engineering Systems